栈和队列学习笔记(21.10.12)
Posted 未定_
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了栈和队列学习笔记(21.10.12)相关的知识,希望对你有一定的参考价值。
以下的栈和队列不是STL。
栈和队列
栈
一、栈的定义
栈:仅在表的一端进行插入和删除操作的线性表。
栈顶:插入和删除的一端
栈底:栈顶的另一端
栈的特点:后进先出
二、顺序栈
利用数组实现栈的顺序存储。
数组标号小的一端作为栈底,另一端为栈顶。top为-1时为空栈。
const int maxsize=100;
class SeqStack
{
public:
SeqStack();
~SeqStack();
void Push(int x);//入栈
int Pop();//出栈
int GetTop();//取栈顶
int Empty();
private:
int data[maxsize];
int top;
};
SeqStack::SeqStack()
{
top=-1;
}
SeqStack::~SeqStack()
{
//顺序栈是静态存储分配,变量退出作用域时自动释放顺序栈所占存储单元,无需销毁
}
void SeqStack::Push(int x)
{
if(top==maxsize-1)
throw"溢出";
data[++top]=x;//top++,data[top];
}
int SeqStack::Pop()
{
int x;
if(top==-1)
throw"溢出";
x=data[top--];//x=data[top],top--;
return x;
}
int SeqStack::GetTop()
{
if(Empty())
throw"空栈";
return data[top];
}
int SeqStack::Empty()
{
if(top==-1)
return 1;
else return 0;
}
三、链栈
用单链表实现栈的基本操作,以单链表的头部作为栈顶,执行插入和删除操作,无需添加头结点。
struct Node
{
int data;
Node *next;
};
class LinkStack
{
public:
LinkStack();
~LinkStack();
void Push(int x);//入栈
int Pop();//出栈
int GetTop();//取栈顶
int Empty();
private:
Node *top;
};
LinkStack::LinkStack()
{
top=NULL;
}
LinkStack::~LinkStack()
{
Node *q=top;
while(top)
{
q=top;
top=top->next;
delete q;
}
}
void LinkStack::Push(int x)
{
Node *s;
s=new Node;
s->data=x;
s->next=top;
top=s;
}
int LinkStack::Pop()
{
Node *p=top;
int x;
if(top==NULL)
throw"下溢";
x=top->data;
top=top->next;
delete p;
return x;
}
int LinkStack::GetTop()
{
if(top==NULL)
throw"下溢";
return top->data;
}
int LinkStack::Empty()
{
if(top==NULL)
return 1;
else return 0;
}
四、拓展:两栈共享空间
利用顺序栈单向延伸的特性,使用一个数组存两个栈,下标0处为栈1的栈底,下标StackSize-1处为栈2的栈底,两栈均向中间延伸。
const int StackSize=100;
class BothStack
{
public:
BothStack();
~BothStack();
void Push(int i,int x);//入栈
int Pop(int i);//出栈
int GetTop(int i);//取栈顶
int Empty(int i);
private:
int data[StackSize];
int top1,top2;
};
BothStack::BothStack()
{
top1=-1;
top2=StackSize;
}
BothStack::~BothStack()
{
}
void BothStack::Push(int i,int x)
{
if(top1==top2-1)
throw"溢出";
if(i==1)
data[++top1]=x;
else data[--top2]=x;
}
int BothStack::Pop(int i)
{
int x;
if(i==1)
{
if(top1==-1)
throw"溢出";
x=data[top1--];
}
else
{
if(top2==StackSize)
throw"溢出";
x=data[top2++];
}
return x;
}
int BothStack::GetTop(int i)
{
if(Empty(i))
throw"空栈";
if(i==1)
return data[top1];
else return data[top2];
}
int BothStack::Empty(int i)
{
if(i==1)
{
if(top1==-1)
return 1;
else return 0;
}
else
{
if(top2==StackSize)
return 1;
else return 0;
}
}
五、拓展:表达式求值
1.中缀表达式求值
设两个栈,一个用来存运算符,另一个存操作数。
对于运算符栈:
•当扫描到的运算符优先级高于栈顶元素,则运算符入栈。
•否则,从运算符栈弹出栈顶元素,并从操作数栈栈顶弹出两个操作数,进行相关计算并将计算结果存入操作数栈,再将扫描到的低运算符入栈,简单概括为消高入低。
•当扫描到左括号时,在扫描到的±*/优先级均高于左括号,当扫描到右括号时,运算符栈需要弹出符号进行计算,直到弹出左括号停止。
•当扫描到的运算符与栈顶元素相同时,栈中符号的优先级高于扫描符号,需要进行消高入低操作。
•规定定界符#的优先级最低
当运算符栈为空时,操作数栈只有一个数,即为表达式的值。

2.中缀表达式->后缀表达式
设1个运算符栈,操作数直接输出,运算符栈的入栈出栈规则如中缀。

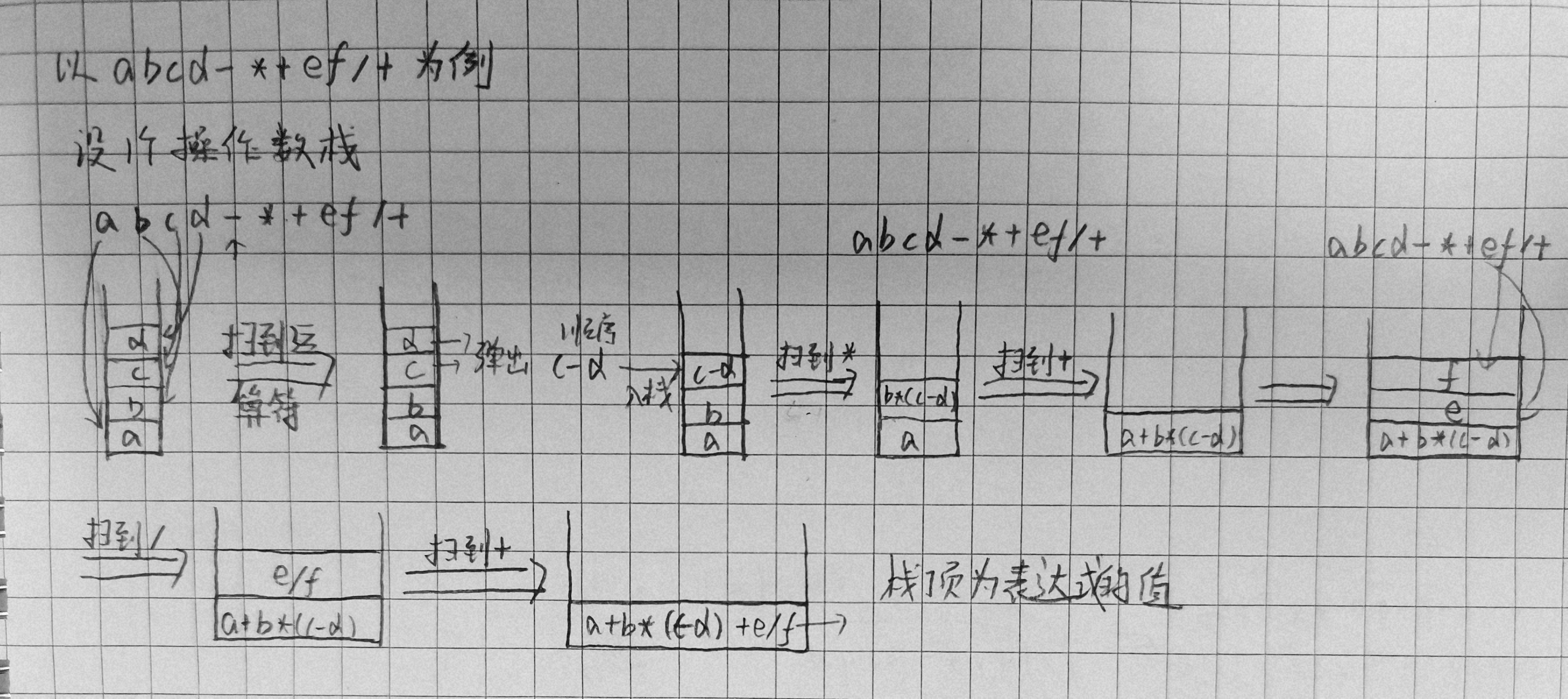
3.后缀表达式求值
也可以看成后缀->中缀,设立一个操作数栈,当扫描到运算符符时,从操作数栈顶弹出两个操作数,进行计算并将结果存入栈顶,注意计算时有顺序,先入栈的数在前。
扫描完毕,操作数栈只有一个数,此时的栈顶元素即为表达式的值。
4.中缀表达式->前缀表达式
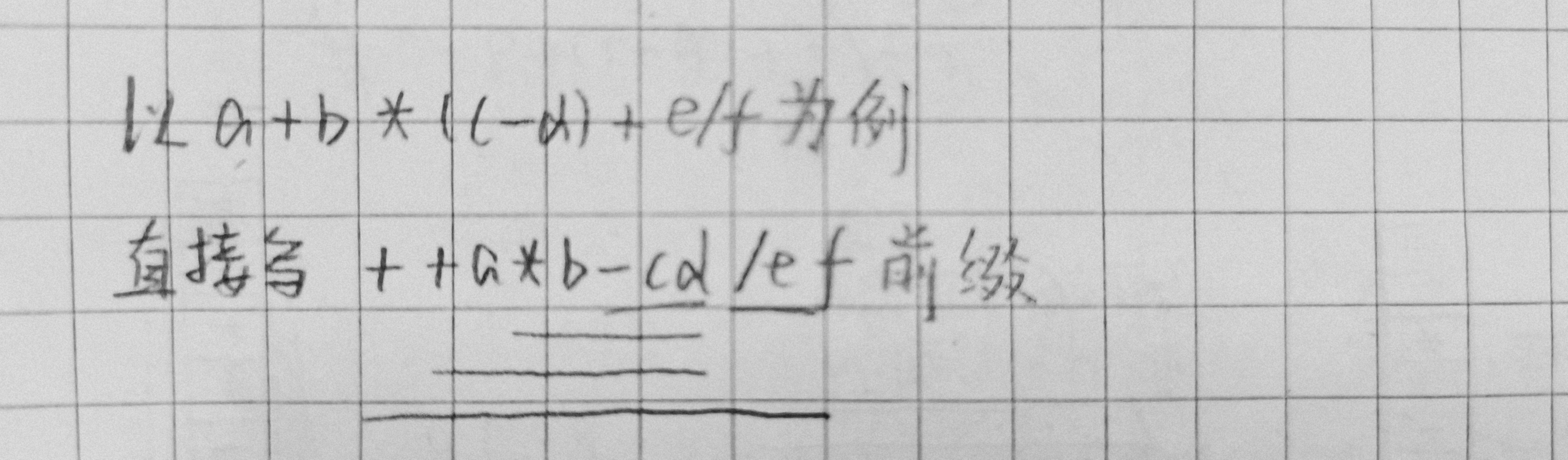
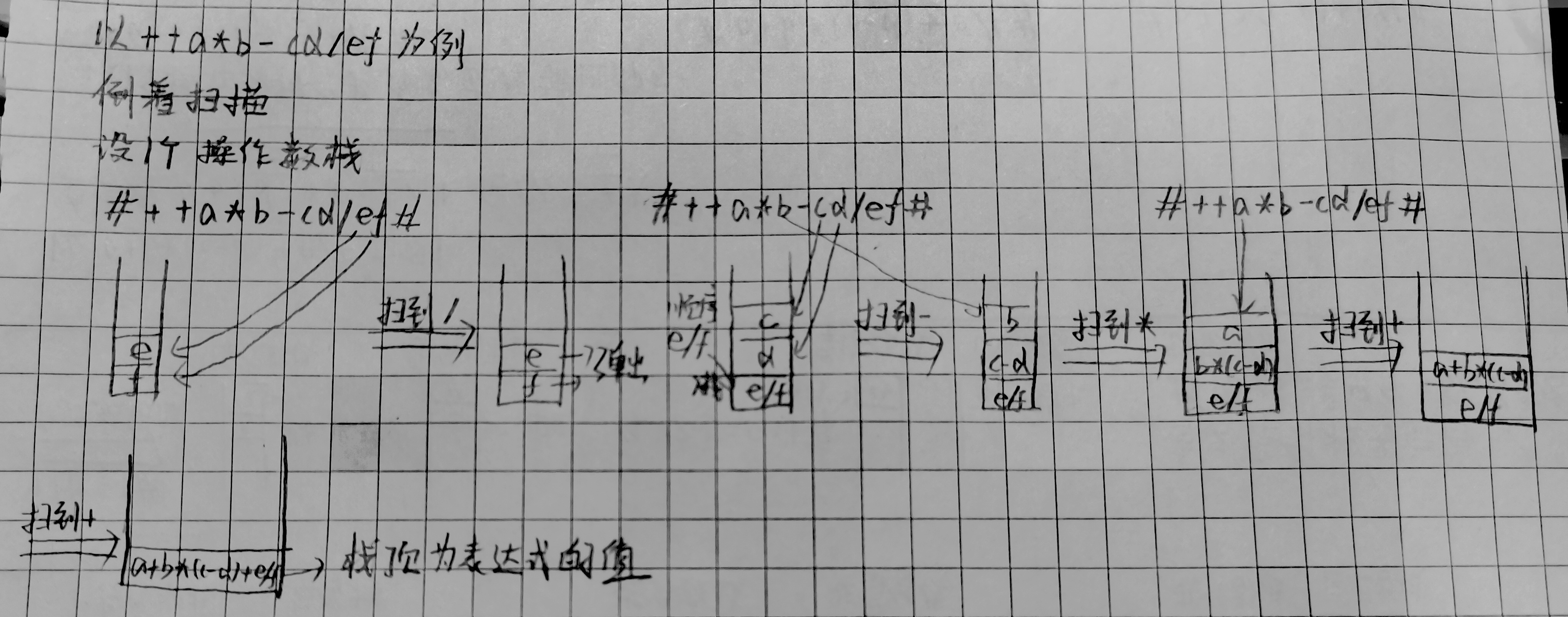
5.前缀表达式求值
也可看成前缀->中缀,设一个操作数栈,前缀表达式倒着扫描,遇到操作数入栈,遇到运算符,从操作数栈顶弹出两个操作数,计算结果存入栈顶,注意计算顺序。
扫描完毕,操作数栈只有一个数,此时的栈顶元素即为表达式的值。
六、拓展:括号匹配
1.简单括号匹配
假设只有小括号,只有(())或()()等才是正确的,(()与)()(等都是错误的。
分析:考虑匹配个数,左括号的个数一定等于右括号的个数才可能匹配。
考虑匹配顺序,先有左括号后有右括号,从左向右扫描时,左括号的个数应该始终大于等于右括号,实际上,每扫描到一个右括号时,我们可以消去一个对应的左括号,保证扫描过程中左括号的个数不为负,且扫描完毕时,左括号个数为0,即匹配成功。
#include<iostream>
using namespace std;
struct Node
{
char data;
Node *next;
};
class LinkStack
{
public:
LinkStack();
~LinkStack();
void Push(char x);//入栈
char Pop();//出栈
char GetTop();//取栈顶
int Empty();
private:
Node *top;
};
LinkStack::LinkStack()
{
top=NULL;
}
LinkStack::~LinkStack()
{
Node *q=top;
while(top)
{
q=top;
top=top->next;
delete q;
}
}
void LinkStack::Push(char x)
{
Node *s;
s=new Node;
s->data=x;
s->next=top;
top=s;
}
char LinkStack::Pop()
{
Node *p=top;
char x;
if(top==NULL)
throw"下溢";
x=top->data;
top=top->next;
delete p;
return x;
}
char LinkStack::GetTop()
{
if(top==NULL)
throw"下溢";
return top->data;
}
int LinkStack::Empty()
{
if(top==NULL)
return 1;
else return 0;
}
void match(LinkStack &s,char ch[])
{
char c;
for(int i=0; ch[i]!=NULL; i++)
{
switch(ch[i])
{
case'(':
case'[':
case'{':
s.Push(ch[i]);
break;
case')':
case']':
case'}':
if(s.Empty())
{
cout<<"多右括号"<<endl;
return ;
}
else
{
c=s.GetTop();
if(ch[i]==')'&&c=='('||ch[i]==']'&&c=='['||ch[i]=='}'&&c=='{')
{
s.Pop();
break;
}
else
{
cout<<"匹配失败"<<endl;
return ;
}
}
}
}
if(s.Empty())
cout<<"匹配成功"<<endl;
else cout<<"多左括号"<<endl;
}
int main()
{
char ch[100];
int n;
cin>>n;
for(int i=0; i<n; i++)
cin>>ch[i];
LinkStack s;
match(s,ch);
}
队列
一、队列的定义
队列:只允许一端插入,另一端删除的线性表。
队尾:允许插入的一端。
队头:允许删除的一端。
队列的特点:先进先出
二、顺序队列
·队列的单向移动性导致数组下标大处空间用尽,但低端仍有空闲空间,为了避免假溢出问题,一般采用循环队列。
·用指针front表示队头,rear表示队尾,rear=(rear+1)%QueueSize。
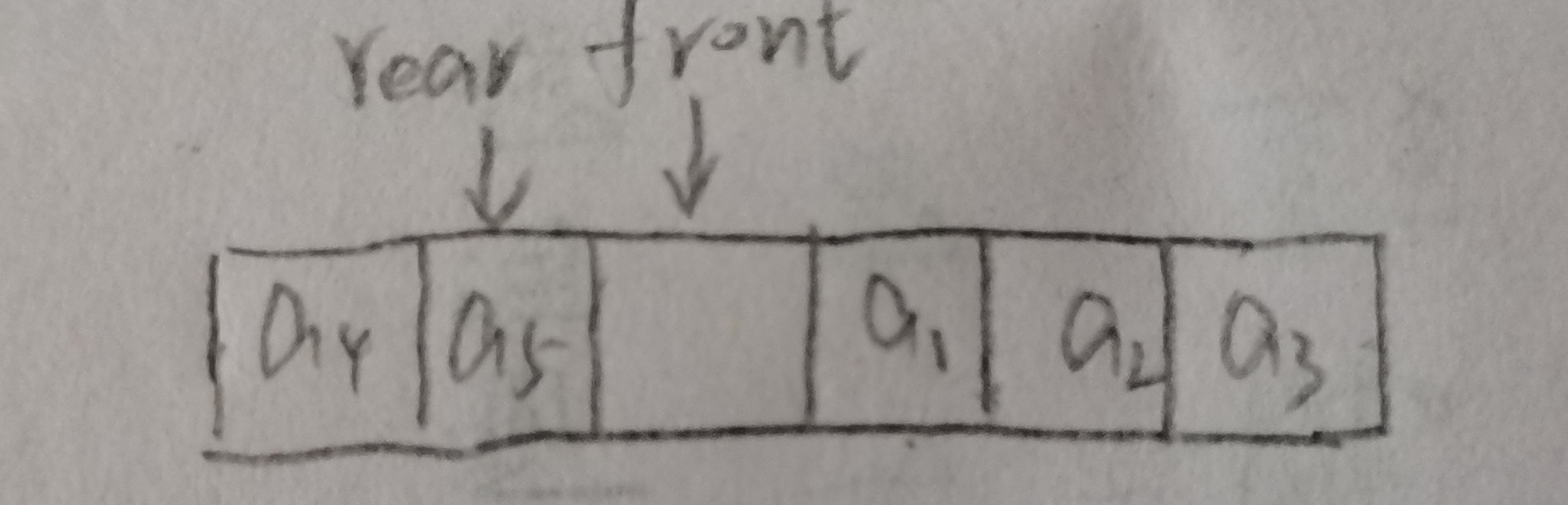
·为了区分队满与队空,当队列中还有一个空位时认为队满:
队满:(rear+1)%QueueSize=front
队空:front=rear
·为了让第一个元素入到下标0处,front和rear可以在-1或数组下标最大处。
·任意时刻队列中元素的个数:(rear-front+QueueSize)%QueueSize
const int QueueSize=100;
class CirQueue
{
public:
CirQueue();
~CirQueue();
void EnQueue(int x);//入队
int DeQueue();//出队
int GetQueue();//取队头
int GetLength();
int Empty();
private:
int data[QueueSize];
int front,rear;
};
CirQueue::CirQueue()
{
rear=front=QueueSize-1;
//为了让第一个元素入到下标0处,front和rear可以在-1或数组下标最大处。
}
CirQueue::~CirQueue()
{
}
void CirQueue::EnQueue(int x)
{
if((rear+1)%QueueSize==front)
throw"上溢";
rear=(rear+1)%QueueSize;
data[rear]=x;
}
int CirQueue::DeQueue()
{
if(front==rear)
throw"下溢";
front=(front+1)%QueueSize;
return data[front];
}
int CirQueue::GetQueue()
{
if(rear==front)
throw"下溢";
return data[(front+1)%QueueSize];
}
int CirQueue::GetLength()
{
if(rear==front)
throw"下溢";
int len=(rear-front+QueueSize)%QueueSize;
return len;
}
int CirQueue::Empty()
{
if(front==rear)
return 1;
else return 0;
}
三、链队列
用单链表表示队列,无需头结点,需头指针指向队头,尾指针指向队尾。
struct Node
{
int data;
Node *next;
};
class LinkQueue
{
public:
LinkQueue();
~LinkQueue();
void EnQueue(int x);//入队
int DeQueue();//出队
int GetQueue();//取队头
int Empty();
private:
Node *front,*rear;
};
LinkQueue::LinkQueue()
{
Node *s=NULL;
s=new Node;
s->next=NULL;
front=rear=s;
}
LinkQueue::~LinkQueue()
{
Node *q=NULL;
while(front!=NULL)
{
q=front;
front=front->next;
delete q;
}
}
void LinkQueue::EnQueue(int x)
{
Node *s=NULL;
s=new Node;
s->data=x;
s->next=NULL;
rear->next=s;
rear=s;
}
int LinkQueue::DeQueue()
{
int x;
Node *p=NULL;
if(rear==front)
throw"下溢";
p=front->next;
x=p->data;
front->next=p->next;
if(p->next==NULL)
rear=front;
以上是关于栈和队列学习笔记(21.10.12)的主要内容,如果未能解决你的问题,请参考以下文章