数据结构入门：时间复杂度

Posted 2021-11-01 长大Leslie

目录

1.算法效率

1.1算法的的复杂度

2.时间复杂度

2.1对时间复杂度的理解

2.2大O的渐进表示法

2.3用实例练习

3 空间复杂度

3.1实例

4.常见的时间复杂度以及复杂度oj练习

---

1.算法效率

如何衡量一个算法的好坏，比如下面的斐波那切数列

long long Fib(N)
{
  if(N<3)
 return 1;
  return Fib(N-1)+Fib(N-2);
}

虽然只有短短的4行代码，当时这真的是简单的吗？

1.1算法的的复杂度

算法在编写成程序后，运行的时候需要消耗时间和空间（内存）资源，因此衡量一个算法的复杂度是从时间和空间两个维度来衡量的，而空间复杂度主要衡量一个算法运行时所需要的额外空间，随着计算机行业的快速发展，计算机的容量已经达到了很高的程度，所以现在没有那么需要关注空间复杂度。

2.时间复杂度

2.1对时间复杂度的理解

在计算机科学中，算法的时间复杂度是一个函数，他定量的描述了一个函数运行需要花的时间（准确的时间是算不出来的）。而一个算法所花费的时间与他的执行次数有关，所以算法中的执行次数就是算法的复杂度

2.2大O的渐进表示法

大O符号（Big O notatiion）：是用于描述函数渐进行为的函数（表示空间复杂度和时间复杂度）

推导大O阶的方法：

1.用常数1取代运行时间中的所有加法常数。

2.在修改后的运行函数中，只保留最高阶。

3.如果最高阶存在且不是1，则去除与个项目相乘的常数，得到的结果就是大O阶。

2.3用实例练习

int BinarySearch(int* a,int n,int x)
{
 assert(a);
  int left=0;
  int right=n-1;
  while(left<right)
{
  int mid=left+((right-left)>>1);
if(a[mid]<x)

left=mid+1;
else if(a[mid]>x)
  right=mid;
else
  return  mid;
}
return -1;
}
  

这是一个二分查找函数，假设这个数组是有序的，求此时的算法的时间复杂度？

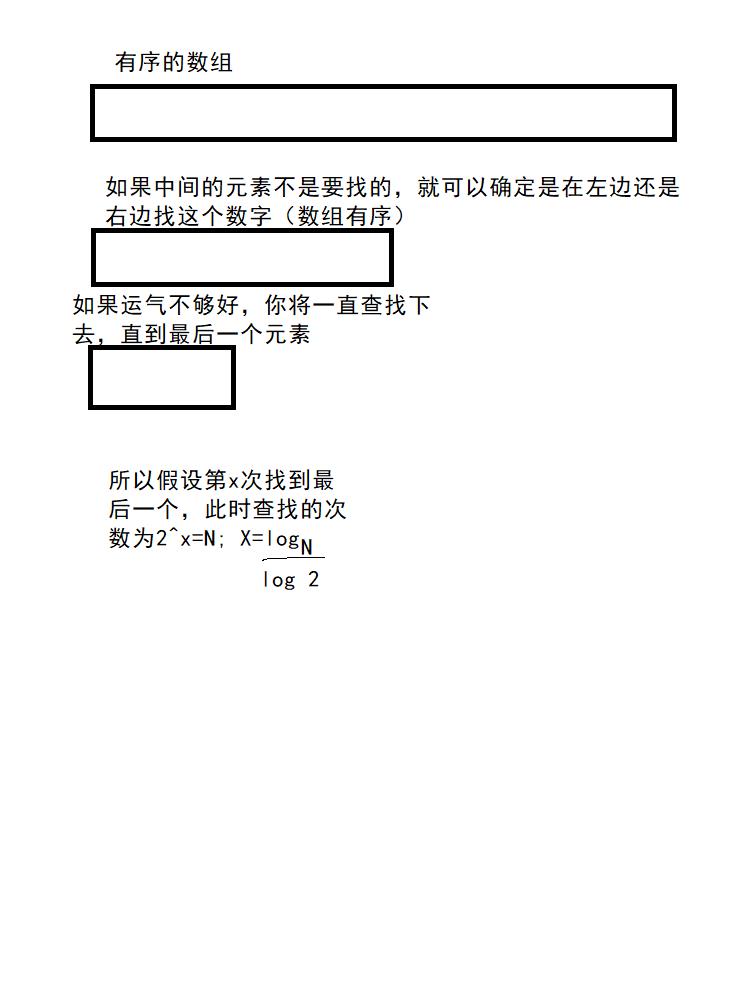
 在实际情况中，一般都是关注的是最坏的情况，所以上面的题是考虑的最坏的情况

实例2

void FUN(int a,int b)
{
 int count=0;
 for(int k=0;k<b;++k)
{
count++;
}
for(int k=0;k<a;k++)
{
count++;
}
printf("%d\\n",count);
}

这段代码中一共运行a+b次，因为a和b是未知的，而且题目中为说明a和b大小的关系（如果a>>b,所以此时的复杂度为O（N）,一般写成N,）所以这时候的时间复杂度为O(2N),根据推导大O的方法，所以此时的时间复杂度为O(N);

例3

long long Fib(size_t N)
{
if(N<3)
return 1;
return Fib(N-1)+Fib(N-2);
}

3 空间复杂度

和时间复杂度一样，空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用空间大小的复杂度。同样，空间复杂度也不计算程序占用多少字节。也用大O渐进表示法。

注意：函数运行时所需要的栈空间（存储参数，局部变量，一些寄存信息等等）在编译期间就已经确定，因此这一些都不算在内，所以空间复杂度只有函数在运行的时候显示申请的额外的空间来确定。

3.1实例

long long* fib(size_t n)
{
if(n==0)
return 0;
long long* fib=(long long*)malloc((n+1)*sizeof(long long));
fib[0]=0;
fib[1]=1;
for(int i=2;i<=n;i++)
{
fib[i]=fib[i-1]+fib[i-2];
}
return fib;
}

这个例子中，每递归一次，程序开辟一次一个额外的空间，一共开辟了N+1个额外空间，所以该例子的空间复杂度为O（N）。

long long fac(size_t n)
{
if(n==0)
return 0;
return fac(n-1)*n;

这个例子调用了N次，开辟了N 个栈帧，每个栈帧使用了常数个空间，空间复杂度为O(N)。

4.常见的时间复杂度以及复杂度oj练习

例1：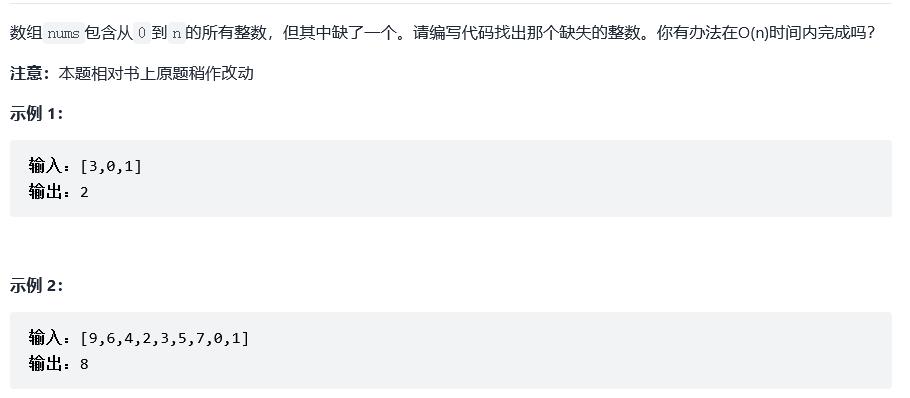

 思路一：根据0~n之间的和为一个等差数列，求出和，再减去数组里面的元素和。数组元素求和一共调用了n次，此时的时间复杂度为O(N)。

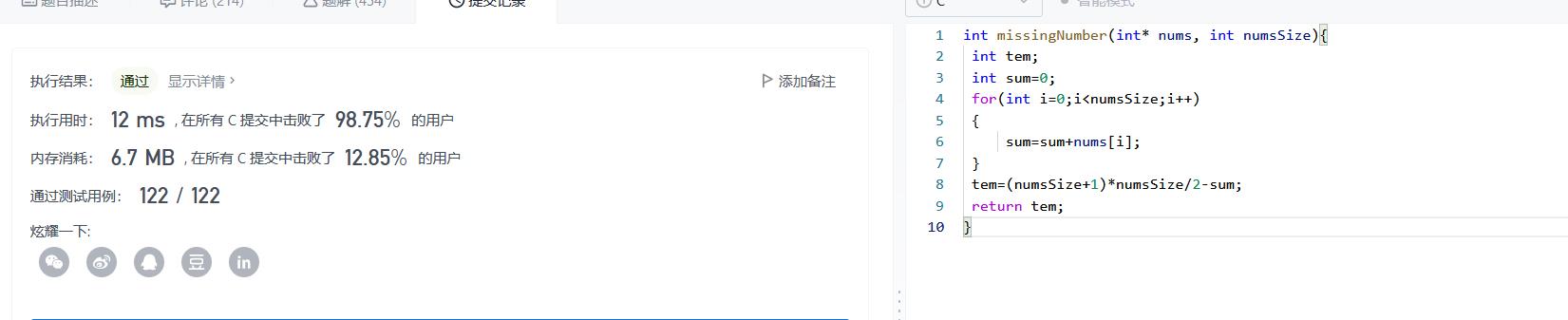
 思路二：

根据异或的特点,创建一个数组包含了o~n的数字，将该数组先和0异或，得到的值再和数组nums进行异或，作何得到的就是两个数组中只出现一次的数字，即数组nums中没有的数字。因为异或是有交换律的，所以不难理解为什么会两个得到那个没有出现过的数字。

例2：

思路一：暴力求解，旋转k次  ；结果：编译不通过

 思路二：开辟额外的空间，用空间换时间

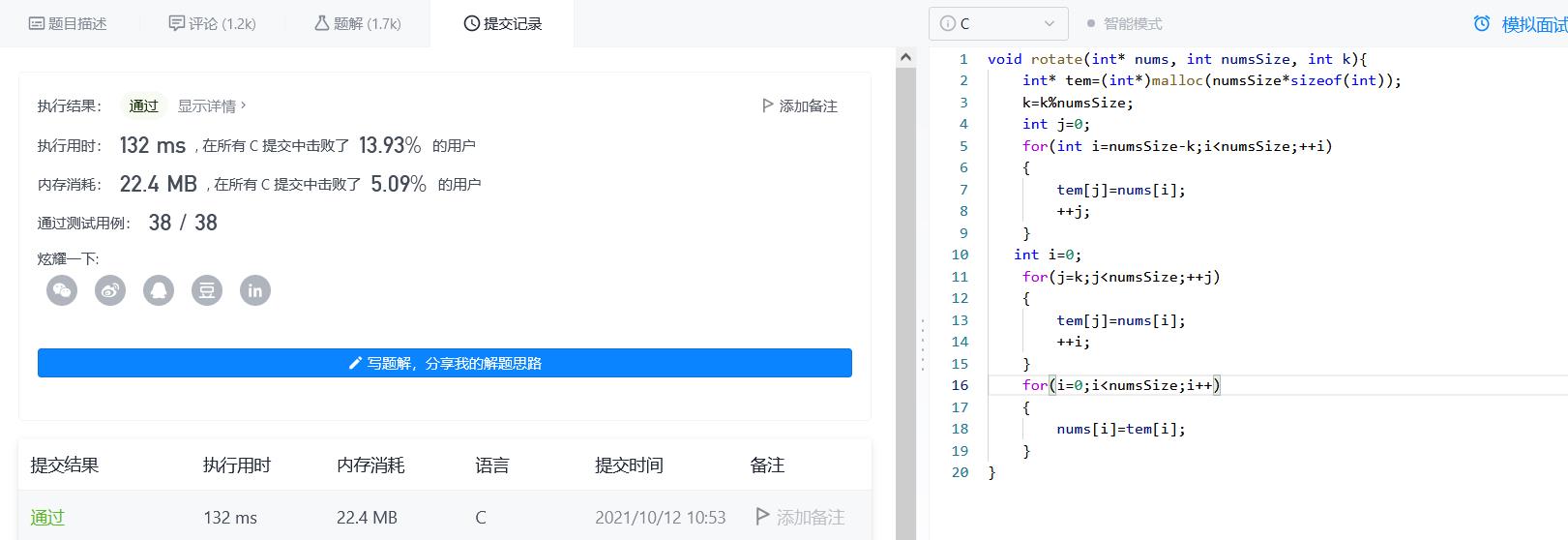
此时的时间复杂度为O（N）,空间复杂度为O(N)；能不能使用O（1）来解决这个问题

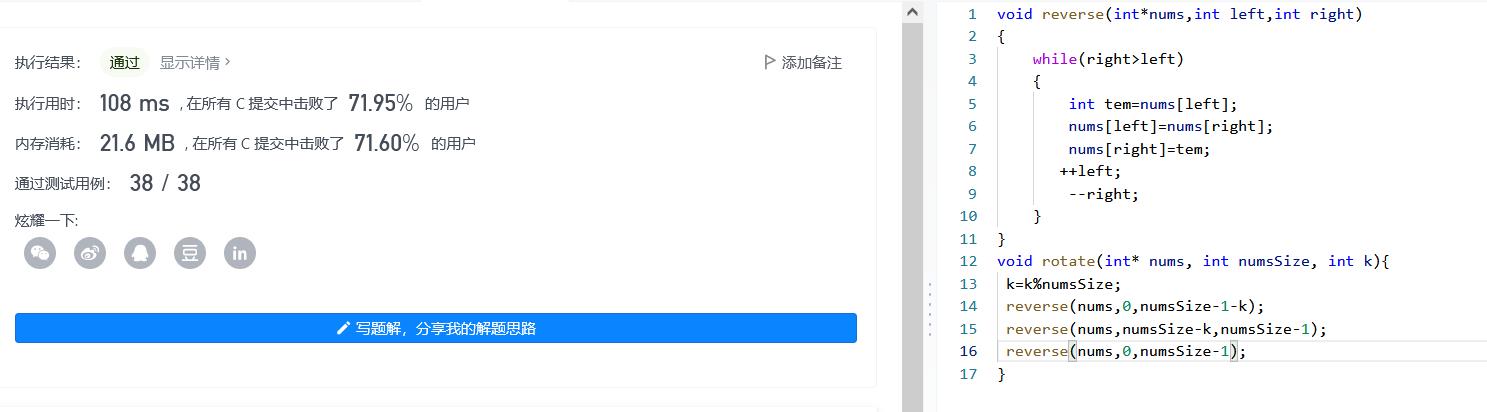
思路三：对前n-k进行逆置，对后面k个进行逆置，最后最整体进行逆置

      此时时间段复杂度为O(N),,空间复杂度为O(1）