week 2——Linear Regression

Posted 2021-10-31 ^_^|

对数据表示做一些规定

$$\begin{gathered} x_j^{(i)}=valueoffeaturejinthe{i}^{th}trainingexample \\ {x}^i=theinput(feature)ofthe{i}^{th}trainingexample \\ m=thenumberoftrainingexamples \\ n=thenumberoffeatures \end{gathered}$$

预测函数，损失函数表示

$hypothesisfunction:h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_n{x}_n$
$costfunction:J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x_i)-y_i{)}^2$

梯度下降法

repeat until convergence：{$${\theta }_j={\theta }_j-\alpha \frac{\partial J(\theta )}{\partial {\theta }_j}={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m((h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)})$$
}

数据归一化

$\frac{x-\mu }{\sigma }$

正规方程法

$\theta =(X^{T}X{)}^{-1}{X}^{T}y$

梯度下降法和正规方程法对比

matlab下演练

假设有数据特征矩阵X为47$\times$ 2表示47个样本，2个特征。同时y表示结果矩阵，大小为为47$\times$ 1。$\theta$ 初始化为47 $\times$ 1的全零向量。

1. 首先，一般会为其增加全1列（即$h(\theta )=w_0+x_1{w}_1+x_2{w}_2$ 一般为$w_0$ 补充$x_0$ 为1）
   X = [ones(m, 1) X];
2. 归一化
   mu = mean(X);
   sigma = std(X);
   X_norm = (X - mu)./sigma;
3. 计算损失函数
   J = sum((X* theta - y).^2)/(2*m);
4. 梯度下降
   for iter = 1:num_iters：
   　　 theta = theta - alpha * (X’((Xtheta) - y)) / m;

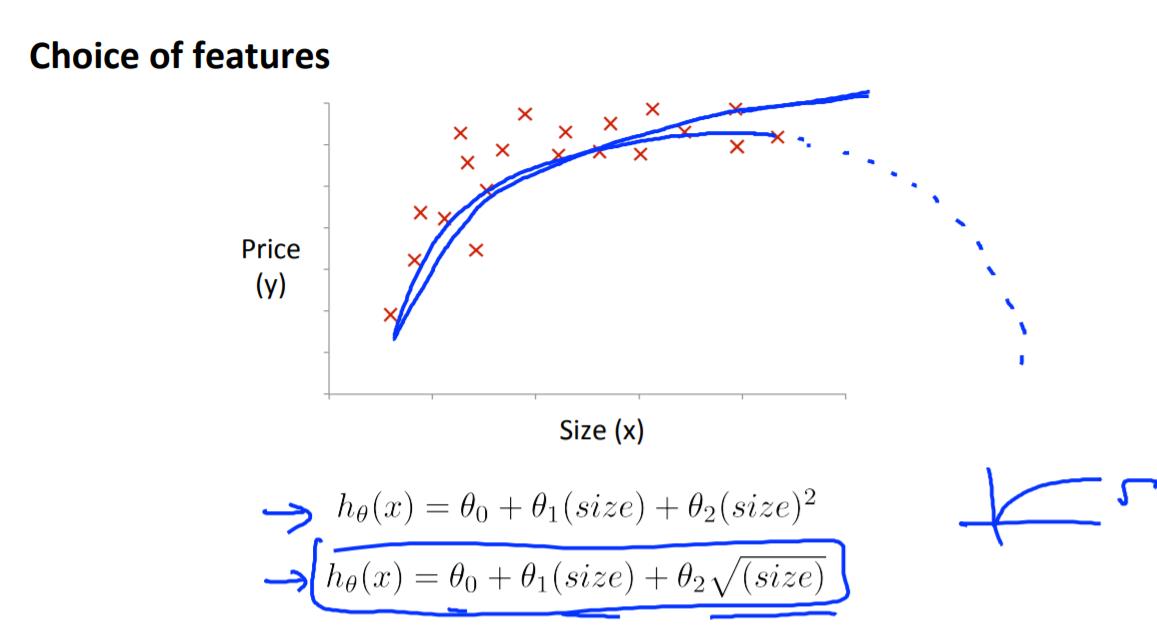
非线性化