极大似然估计原理

Posted 2023-03-08 呆呆象呆呆

文章目录

• 问题引出：
• 重要前提：
• 极大似然估计
• 求解极大似然函数
• 极大似然估计的例子
• 总结

问题引出：

贝叶斯决策
首先来看贝叶斯分类，我们都知道经典的贝叶斯公式：
$$\begin{array}{c}P(w|x)=\frac{p(x|w)p(w)}{p(x)}\end{array}$$

其中：$p(w)$：为先验概率，表示每种类别分布的概率；$p(x|w)$：类条件概率，表示在某种类别前提下，某事发生的概率；而为后验概率，表示某事发生了，并且它属于某一类别的概率，有了这个后验概率，我们就可以对样本进行分类。后验概率越大，说明某事物属于这个类别的可能性越大，我们越有理由把它归到这个类别下。

详细的讲解可以看一下我的另外一篇blog概率图模型（3）朴素贝叶斯分类

但是在实际问题中并不都是这样幸运的，我们能获得的数据可能只有有限数目的样本数据，而先验概率$p\left(w_i\right)$和类条件概率$p\left(x|w_i\right)$(各类的总体分布)都是未知的。根据仅有的样本数据进行分类时，一种可行的办法是我们需要先对先验概率和类条件概率进行估计，然后再套用贝叶斯分类器。

先验概率$p\left(w_i\right)$的估计较简单，有如下几种方法
1、每个样本所属的自然状态都是已知的（有监督学习）
2、依靠经验
3、用训练样本中各类出现的频率估计

类条件概率$p\left(x|w_i\right)$的估计（非常难），原因包括：概率密度函数包含了一个随机变量的全部信息；样本数据可能不多；特征向量$x$的维度可能很大等等。总之要直接估计类条件概率的密度函数很难。解决的办法就是，把估计完全未知的概率密度$p\left(x|w_i\right)$转化为估计参数。==这里就将概率密度估计问题转化为参数估计问题，极大似然估计就是一种参数估计方法。==当然了，概率密度函数的选取很重要，模型正确，在样本区域无穷时，我们会得到较准确的估计值，如果模型都错了，那估计半天的参数，肯定也没啥意义了。

重要前提：

上面说到，参数估计问题只是实际问题求解过程中的一种简化方法（由于直接估计类条件概率密度函数很困难）。所以能够使用极大似然估计方法的样本必须需要满足一些前提假设。
重要前提：训练样本的分布能代表样本的真实分布。每个样本集中的样本都是所谓独立同分布的随机变量 (iid条件)，且有充分的训练样本。

极大似然估计

极大似然估计的原理，用一张图片来说明，如下图所示：

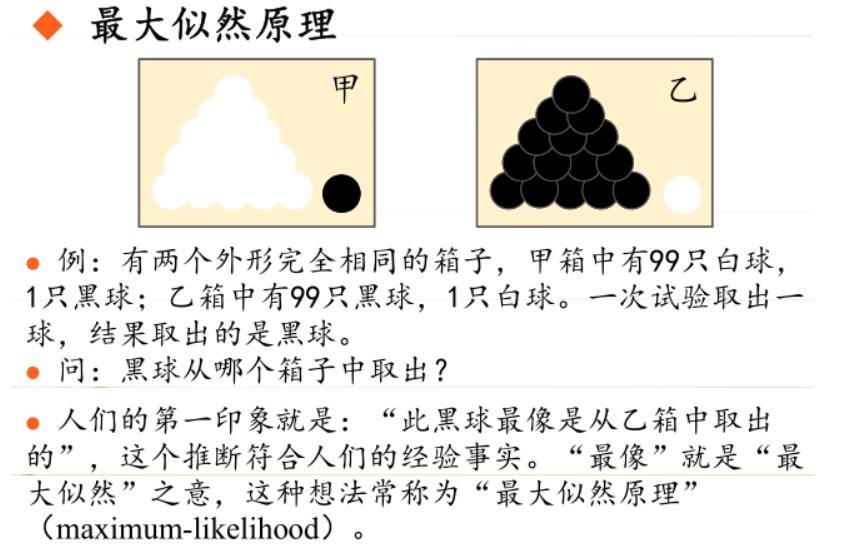
总结起来，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。
原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。
由于样本集中的样本都是独立同分布，可以只考虑一类样本集$D$，来估计参数向量$\theta$。记已知的样本集为：
$$D=x_1,x_2,\cdots ,x_N$$
似然函数（linkehood function）：联合概率密度函数$p(D|\theta )$称为相对于$x_1,x_2,\cdots ,x_N$的$\\theta $的似然函数。
$$l(\theta )=p(D|\theta )=p\left(x_1,x_2,\cdots ,x_N|\theta \right)=\prod _{i=1}^{N}p\left(x_i|\theta \right)$$
公式解析：在不同$\theta$下似然函数的值为在这种样本分布情况下由此时的$\theta$通过联合概率分布得出，联合概率分布又因为样本之间独立，转换成乘法模型。

如果$\hat{\theta }$是参数空间中能使似然函数$l(\theta )$最大的$\theta$值，则应该是“最可能”的参数值，那么就是$\theta$的极大似然估计量。它是样本集的函数，在不同的样本集$D$中，有不同的参数估计，记作：
$$\hat{\theta }=d\left(x_1,x_2,\cdots ,x_N\right)=d(D)$$
$\hat{\theta }\left(x_1,x_2,\cdots ,x_N\right)$即为极大似然函数估计值。

求解极大似然函数

ML估计：求使得出现该组样本的概率最大的$\theta$值。
$$\hat{\theta }=\arg \underset{\theta }{\max }l(\theta )=\arg \underset{\theta }{\max }\prod _{i=1}^{N}p\left(x_i|\theta \right)$$
实际中为了便于分析，定义了对数似然函数：
$$\begin{array}{c}H(\theta )=\ln l(\theta )\\ \hat{\theta }=\arg {\max }_{\theta }H(\theta )=\arg {\max }_{\theta }\ln l(\theta )=\arg {\max }_{\theta }{\sum }_{i=1}^N\ln p\left(x_i|\theta \right)\end{array}$$
1、当未知参数只有一个（$\theta$为标量）
在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解：
d l ( θ ) d θ = 0 或 者 等 价 于 d H ( θ ) d θ =