K最近邻算法

Posted 2021-10-31 shi_zi_183

KNN算法

分类是数据挖掘领域中的一种重要的技术，它是从一组已知的训练样本中发现分类模型，并且使用这个分类模型来预测待分析样本。建立一个有效的 分类算法模型最终将待分类的样本进行处理是非常有必要的。
目前常用的分类算法主要有：朴素贝叶斯分类算法、支持向量机分类算法、KNN最近邻算法、神经网络算法、已经决策树等等。

KNN的基本思想

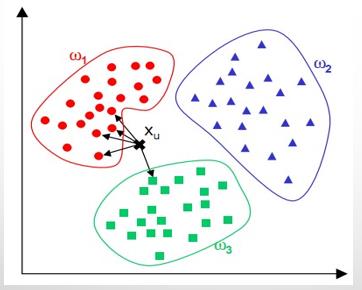
根据距离函数计算待分类样本X和每个训练样本的距离(作为相似度)，选择与待分类样本的距离最小的K个样本作为X的K个最近邻，最后以X的K个最近邻中的大多数所属的类别作为X的类别。
KNN可以说是一种最直接的用来分类未知数据的方法。
简单来说，KNN可以看成：有那么一堆你已经知道分类的数据，然后当一个新数据进入的时候，就开始跟训练数据里的每个点求距离，然后挑出离这个数据最近的K个点，看看这K个点属于什么类型，然后用少数服从多数的原则，给新数据归类。

KNN算法的实现

1）问题描述
数据集：iris.data标准数据集。
采用KNN算法对iris.data分类。为了操作方便，对各组数据添加rowNo属性，第一组rowNo=1，共有150组数据，选择rowNo模3不等于0的100组作为训练数据集，剩下的50组做测试数据集。
2）实现步骤：

1. 初始化距离为最大值
2. 计算未知样本和每个训练样本的距离dist
3. 得到目前k个最临近样本中的最大距离maxdist
4. 如果dist小于maxdist，则将该训练样本作为K-最近邻样本
5. 重复步骤2、3、4，直到所有未知样本和所有训练样本的距离都算完
6. 统计K-最近邻样本中每个类标号出现的次数
7. 选择出现频率最大的类标号作为未知样本的类标号。

KNN的优缺点

优点：

1. 算法思路较为简单，易于实现
2. 当有新样本要加入训练集中时，无需重新训练
3. 计算时间和空间线性于训练集的规模
   缺点：
4. 分类速度慢：
   KNN算法的时间复杂度和存储空间会随着训练集规模和特征的增大而快速增加。因为每次新的待分析样本都必须与所有训练集一同计算比较相似度，以便取出靠前的K个已分类样本。整个算法的时间复杂度可以用O(m*n)标识，其中m是选出的特征项的个数，而n是训练集样本的个数。
5. 各属性的权重相同，影响了准确率：
   当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。该算法只计算"最近的"邻居样本，如果某一类的样本数量很大，那么可能目标样本并不接近这类样本，却会将目标样本分到该类下，影响分类准确率。
6. 样本库容量依赖性较强
7. K值不好确定
   K值选择过小，得到的近邻数过少，会降低分类精度，同时也会放大噪声数据的干扰；而K值选择过大，如果待分类样本属于训练集中包含数据较少的类，那么在选择k个近邻的时候，实际上并不相似的数据也被包含进来，造成噪声增加而导致分类效果的降低。

KNN的一些改进策略

• 从降低计算复杂度的角度
  1. 当样本容量较大以及特征属性较多时，KNN算法分类的效率就将大大降低。可以采用以下方法进行改进。
  2. 如果在使用KNN算法之前对样本的属性进行约简，删除那些对分类结果影响较小的属性，则可以用KNN算法快速地得出待分类样本地类别，从而可以得到更好地效果。
  3. 粗糙集理论在用于决策表地属性约简时，可在保持决策表中决策能力不变地前提下，删除其中不相关的冗余属性。
  4. 缩小训练样本的方法
  5. 通过聚类，将聚类所产生的中心点作为新的训练样本
• 从优化相似度度量方法的角度
  1. 基本的KNN算法基于欧几里得距离来计算样本的相似度，这种方法对噪声特征非常敏感。
  2. 为了改变传统KNN算法中特征作用相同的缺陷，可在度量相似度的距离公式中给特征赋予不同权重，特征的权重一般根据各个特征在分类中的作用设定。
• 从优化判决策略的角度
  传统的KNN算法的决策规则的缺点是，当样本分布不均匀（训练样本各类别之间数目不均衡，或者即使基本数目接近，由于其所占区域大小的不同）时，只按照前K个邻近顺序而不考虑它们的距离，会造成误判，影响分类的性能。可以采用均匀化样本分布密度的方法进行改进。
• 从选取恰当k值得角度
  由于KNN算法中几乎所有得计算都发生在分类阶段，而且分类效果很大程度上依赖于k值得选取。而目前为止，比较好得选k值的方法只能是通过反复试验调整。