CS224W摘要16.Advanced Topics on GNNs

Posted 2021-10-30 oldmao_2000

文章目录

• Limitations of GNN
• • Limitation 1
  • Limitation 2
  • How to fix them
  • 错误思路
• Position-aware GNNs
• • Structure-aware task
  • Position-aware task
  • 锚点原力解决方案
  • 锚点集
  • 位置信息的处理
• Identity-aware GNNs
• • Failure in three level
  • 解决思路
  • Identity-aware GNN[^2]
  • ID-GNN-Fast
  • 小结
• GNN的鲁棒性
• • GNN对抗攻击类型
  • • 直接攻击
    • 间接攻击
  • GNN对抗攻击
  • • 总览
    • 数学表达
  • GCN对抗攻击实验

CS224W: Machine Learning with Graphs
公式输入请参考： 在线Latex公式

Limitations of GNN

主要两个。

Limitation 1

两个节点有相同邻居或邻域结构，按理其表征应该相同：

但是实际上不一定，因为有些邻域相同但是表征不应该相同，特别是对称图结构，例如：


PS这个图上点虽然不清楚具体是哪里，但是看到NY的街道非常规整，因此也和上面的网格图类似。
这类任务叫：Position-aware tasks

Limitation 2

两个节点不同相同邻居或邻域结构，按理其表征应该不相同：

关于这个在第九讲里面有过证明，GNN的上限是WL test，因此普通GNN无法很好表达环状图形长度：

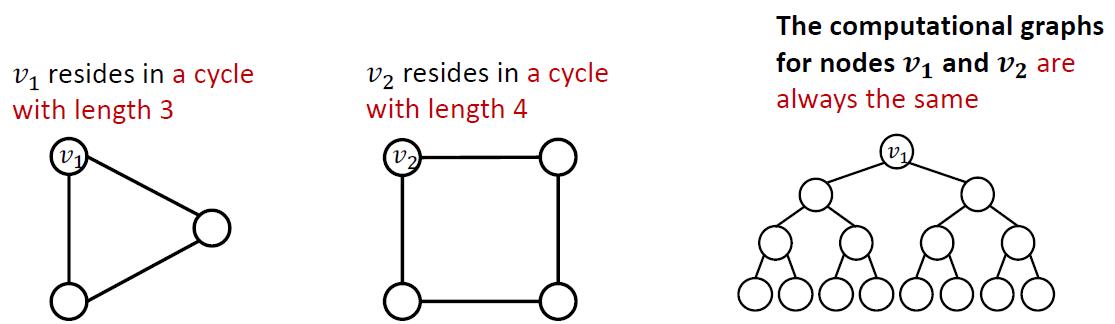
How to fix them

对于问题1：Create node embeddings based on their positions in the graph.
方法：Position-aware GNNs
对于问题2：Build message passing GNNs that are more expressive than WL test.
方法：Identity-aware GNNs
大概思路：
两个不同的输入，节点、边、图都标记得不一样。希望得到一个模型，获得不同的表征，例如：

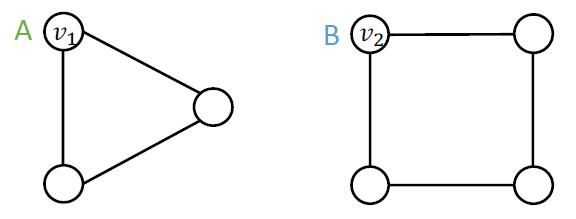
Two inputs: nodes $v_1$ and $v_2$.
Different labels: A and B.
Goal: assign different embeddings to nodes $v_1$ and $v_2$.

错误思路

非常intuition，直接每个节点不同独热编码：

得到的计算图当然也不一样，我们也会得到不同的表征：

但是这个方法行不通，因为：
1.scalability差，每个节点需要$O(N)$维度来作为表征，$N$是节点数量，大型图不能这样玩，说好映射到低维空间的哈。
2.没有inductive，这个玩法只能在当前图玩，新点加入全部要重新计算一遍。

Position-aware GNNs

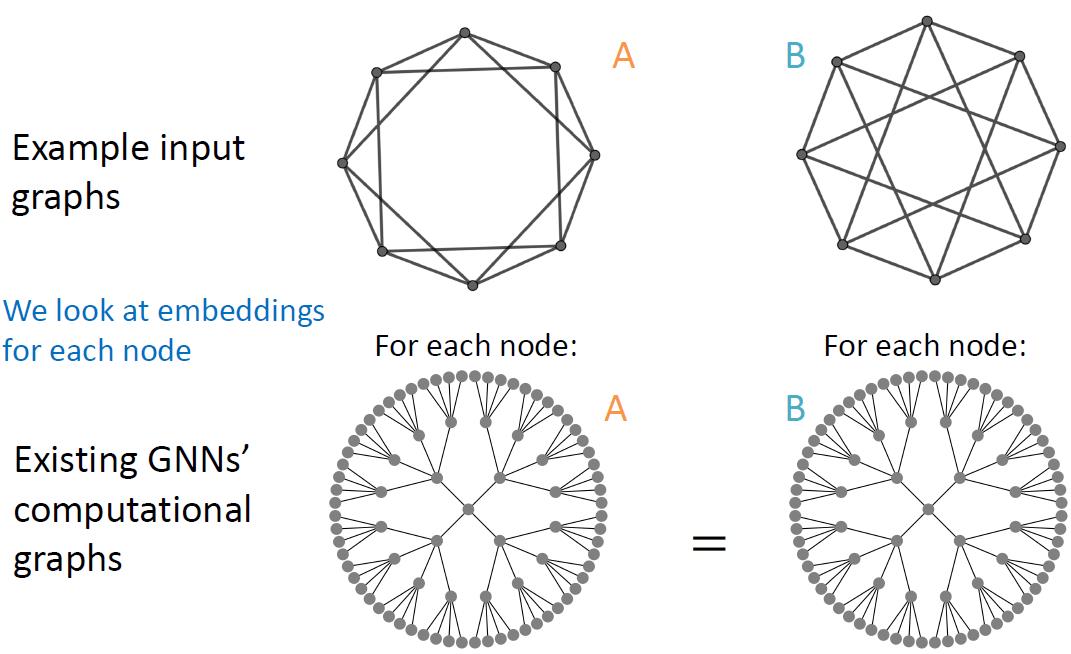
Structure-aware task

节点按他们的结构进行标签，例如两边的B都有两个A做邻居。
我们常见的GNN对于Structure-aware task都适用，包括：GCN，GraphSage，GAT等。因为A和B的计算图明显不一样。

Position-aware task

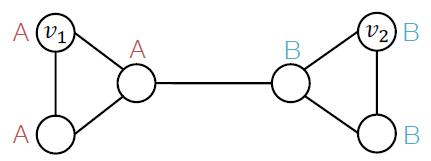
节点按他们的位置进行标签，常见的有社区检测任务，上图左右两边是不同两个社区，因此他们各自标记也不一样。
普通GNN没法玩，因为上图中的A和B有相同的计算图（不考虑额外特征的情况下，GNN无法区分两个点的表征）：

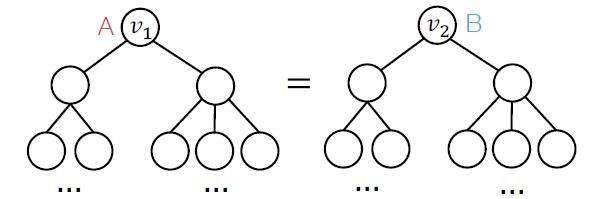
锚点原力解决方案

就好比要比较两个物体的大小，必须要有参照物一样的原理，锚点就是这里的参照物。
随机选择一个节点$s_1$作为锚点，通过两个节点$v_1,v_2$相对锚点$s_1$的位置不同来解决Position-aware task，例如：

当然如果不止选定一个锚点，那么结果会更加鲁棒，相当于从不同坐标系（角度）来看节点位置：

锚点集

下面给出具体的Position-aware task解决方案描述：、
把节点到锚点的距离可以表示为到某个锚点集的距离，例如：下图中的锚点集 s 3 = { s 1 , v 3 } , s i z e = 2 s_3=\\{s_1,v_3\\},size=2 s3​={s1​,v3​},size=2

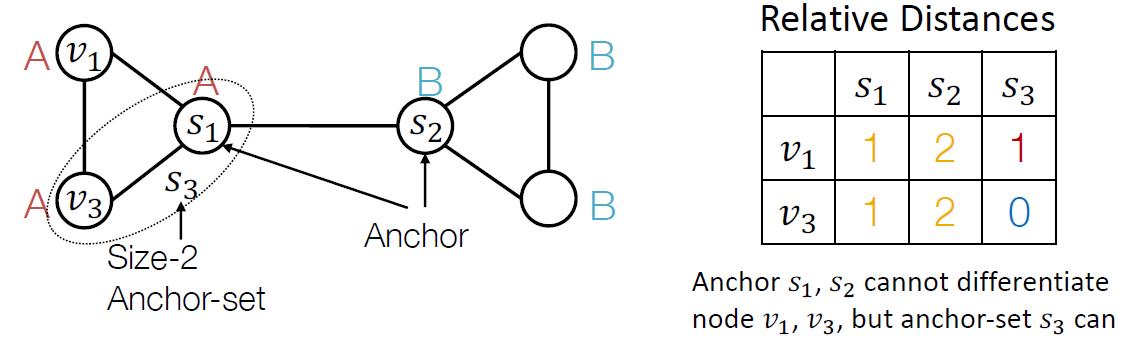
锚点集可使用更少的点，提供更精确的位置估计。
而且位置信息表征可以用距离来表示：

PS：锚点集尺寸大小选择通常是1.2.4.16这样增长的，然后组合起来，具体选择估计要实验，节点是随机选的（但是应该是相邻的）。

位置信息的处理

通过上面的方法我们了解了如何通过锚点集来获得节点的位置表征，这样做在实际效果上没有什么大问题，但是由于锚点集的变化，会引起节点的位置表征在维度，顺序上的变化，这个缺点会导致位置表征与NN不匹配的情况出现，例如，你训练好了一个吃100维输入的NN，然后锚点集变化，位置表征变成80维，NN就废了。
更加rigorous的解决方案是将通过锚点集得到的位置表征重新处理一下，例如经过一些aggregation处理，使得位置表征的维度固定，顺序无关。具体看相关论文¹。

Identity-aware GNNs

这个主要是针对前面讲的structure-aware tasks的，虽然说传统GNN在这个任务上比较擅长，但是还有特殊的情况无法处理，共有三种情况：

Failure in three level

Node level failure

Edge level failure

Graph level failure

解决思路

将要表征的节点上色后展开为计算图：

对于节点级别，可以帮助node classification

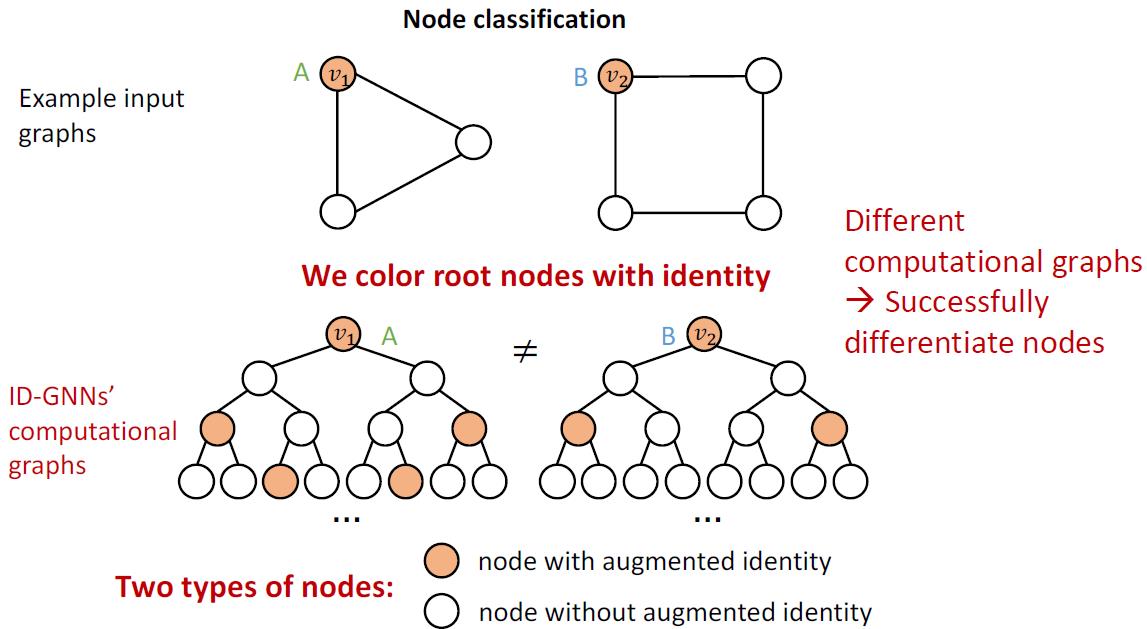
边级别可以帮助link prediction

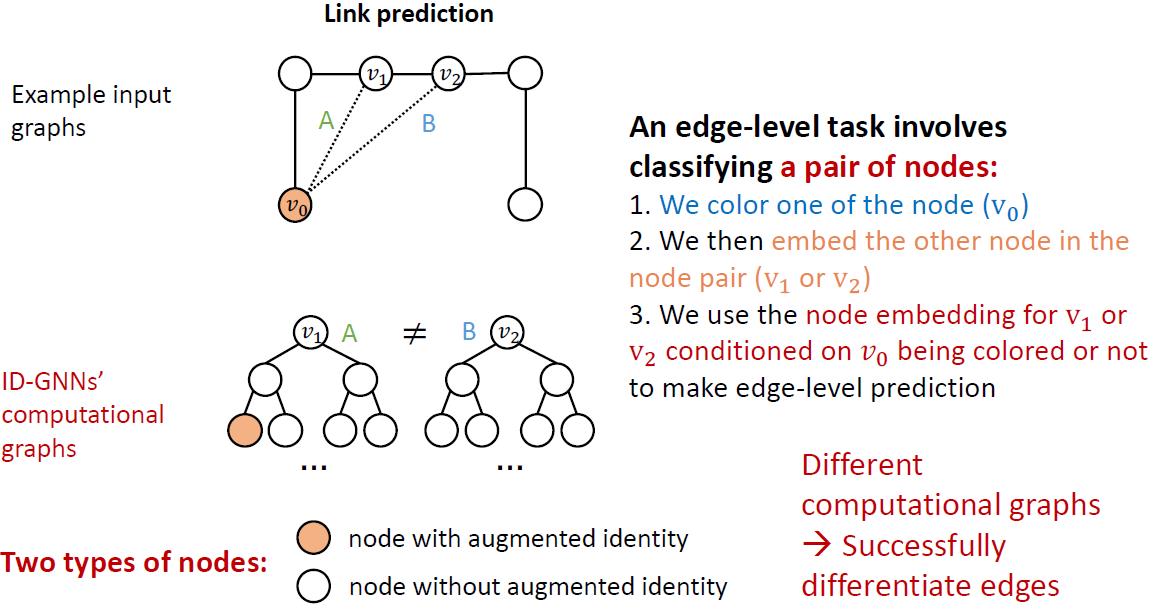
图级别可以帮助graph classification

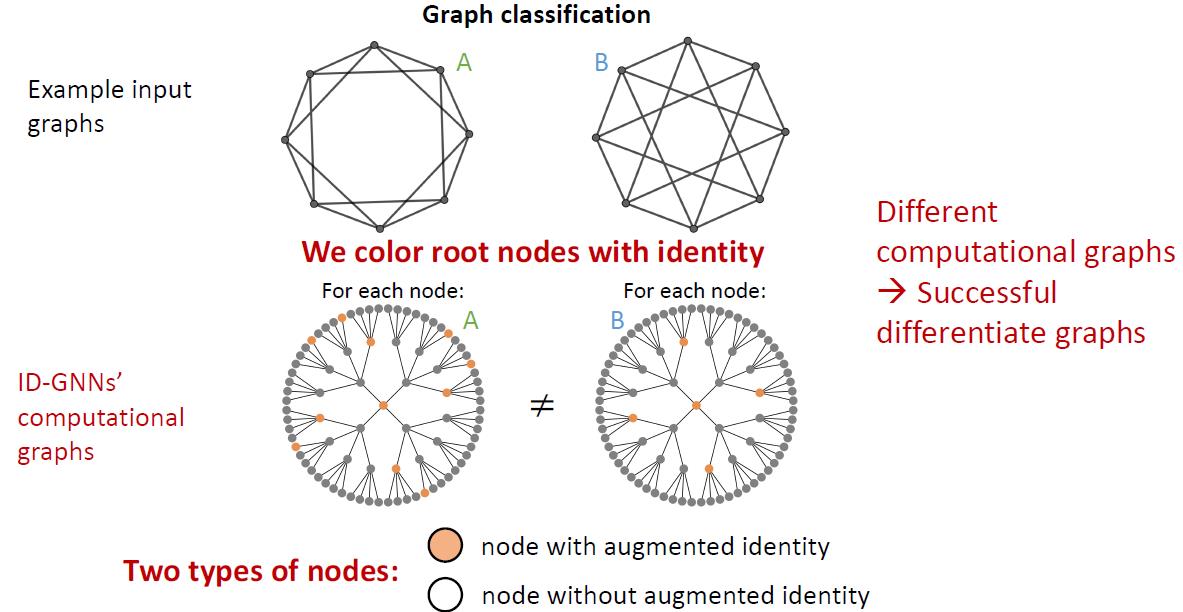
思路有了，上模型：

Identity-aware GNN²

在表征计算过程中利用节点上色来鉴别不同节点。主要思想是：异质消息传递（看图例貌似是作用在目标节点和其他节点上？）。
正常的GNN会使用相同的消息聚合函数：

ID-GNN使用不同的消息聚合函数，不同函数代表不同颜色。

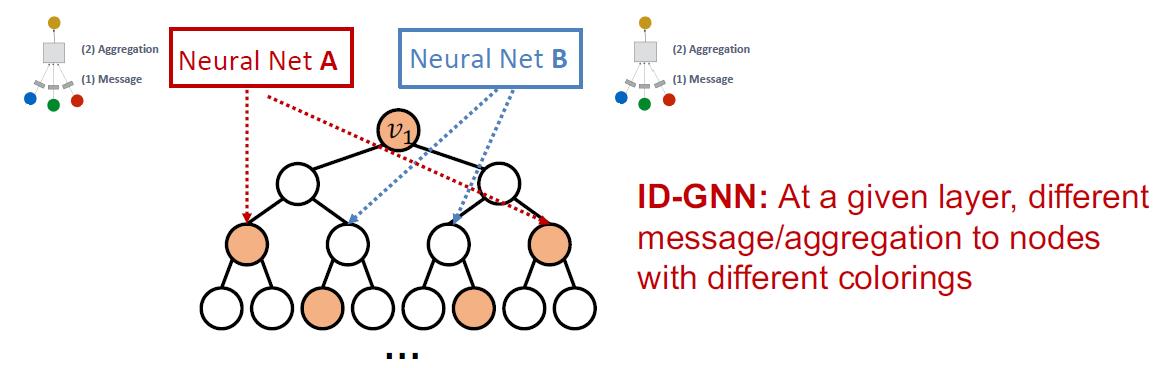
看下原理，假定两个节点有相同计算图，并有颜色标识（也不能说不同颜色，不同颜色就变成独热编码了，就是加上了标记即可），用了不同的消息聚合函数后，会得到不同的表征：

相对于GNN，ID-GNN可以识别出环形图周期，而GNN不行

ID-GNN-Fast

改进在不需要额外使用异质消息聚合函数，直接使用每一层计算图中目标节点出现的次数作为identity表征：

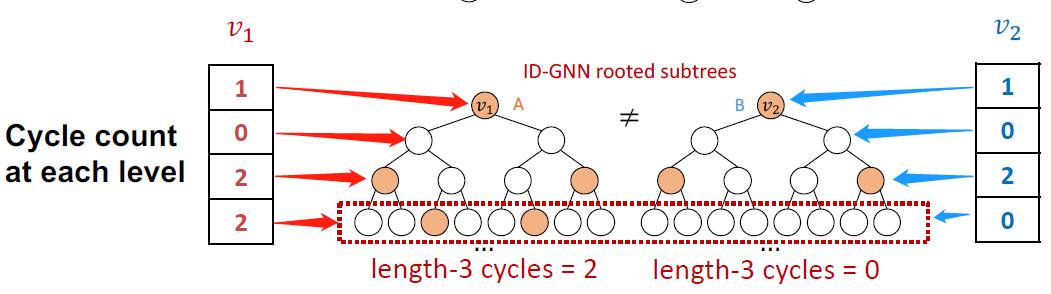
例如红色的$v_1$节点的identity information就是第一层出现1次，第二层出现0次，以此类推。把这个identity information可以做为节点的augmented feature，这样就可以用在各种不同的GNN模型（GCN, GraphSAGE, GIN）中了。

小结

ID-GNN是第一个基于消息传递机制，并且表达能力比1-WL test还牛的模型，而且还可以用于现有的模型。
DGL和PyG已经有ID-GNN的实现了。

GNN的鲁棒性

这节貌似讲对抗攻击：adversarial attacks
这个在图像上已经有过类似的案例：

在NLP和声音处理领域也有类似案例。
从本质上看，是模型预测出错了，鲁棒性不好。对于GNN而言，也存在类似问题，常见的对抗攻击出现在：
Recommender systems
Social networks
Search engines

GNN对抗攻击类型

分直接攻击和间接攻击。先给出简单定义：
目标节点： $t\in V$，攻击者想要修改标签的节点。
攻击节点（可有多个）：$S\subset V$，攻击者能修改的节点

直接攻击

攻击节点就是目标节点： S = { t } S=\\{t\\} S={t}
1.修改目标节点特征

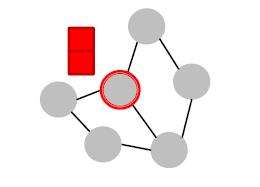
2.1为目标节点添加连接。例如：买粉丝

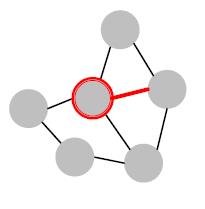
2.2为目标节点去掉连接。例如：掉粉

间接攻击

目标节点不在攻击节点中：$t\notin S$
1.修改攻击节点特征，例如劫持目标节点的邻居

2.1为攻击节点添加与目标节点的连接。

2.2去掉攻击节点不相关的边。

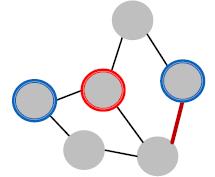
GNN对抗攻击

总览

攻击者目标：
$$\begin{gathered} \text{Maximize(修改目标节点的标签预测结果)} \\ 条件：改动最小\text{manipulation is small} \end{gathered}$$
改动越大，越容易被发现，成功的攻击往往是比较隐蔽的攻击。

数学表达

以GCN的节点分类任务为例。
原始图的邻接矩阵为$A$，特征矩阵为$X$；
攻击后的邻接矩阵为$A^{\prime }$，特征矩阵为$X^{\prime }$。
假定：
$$(A,X)\approx (A^{\prime },X^{\prime })$$
也就是攻击后图的改动非常小，并不影响原有图的统计属性，例如：度分布，特征统计等。
记目标节点为：$v\in V$
GCN对于原图的目标函数为：
$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmin}}{\mathcal{L}}_{train}(\theta ;A,X)$$

这里的训练过程设置的参数$\theta$是攻击者无法改变的，模型训练好后进行部署，其神经网络参数不可改变，我们攻击者只能改变输入的图结构³。
GCN对于攻击前目标节点$v$的原始预测分类结果为：
$$c_v^{\ast }=\underset{c}{\mathrm{argmax}}{f}_{{\theta }^{\ast }}(A,X{)}_{v,c}$$
这里的$c_v^{\ast }$是攻击目标节点$v$的预测分类对应的最大概率（softmax的结果中的最大值）。

GCN对于被篡改后图的目标函数为：
$${\theta }^{\ast }{}^{\prime }=\underset{\theta }{\mathrm{argmin}}{\mathcal{L}}_{train}(\theta ;A^{\prime },X^{\prime })\text{\hspace{1em}(1)}$$
GCN对于攻击后目标节点$v$的攻击预测分类结果为：
c v ∗ ′ = arg max ⁡ c f θ ∗ ′ ( A ′ , X ′ ) v , c c_v^{*}{'}=\\argmax_cf_{\\theta^{*}{'}}(A',X')_{v,c} cv∗​′=cargmax以上是关于CS224W摘要16.Advanced Topics on GNNs的主要内容，如果未能解决你的问题，请参考以下文章

CS224W摘要总纲（已完结）

CS224W摘要总纲（已完结）

CS224W摘要10.Knowledge Graph Embeddings

CS224W摘要03.Node Embedding

CS224W摘要05.Message passin and Node classification

CS224W摘要15.Deep Generative Models for Graphs