GPU 渲染管线与着色器 大白话总结 ---- 一篇就够
Posted 长江很多号
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了GPU 渲染管线与着色器 大白话总结 ---- 一篇就够相关的知识,希望对你有一定的参考价值。
码字不易,不求打赏,不求打脸,只求转载注明出处:
https://blog.csdn.net/newchenxf/article/details/119803489
GPU 渲染管线与着色器 大白话总结 ---- 一篇就够
1 前言
做图形图像,就要懂GPU;
要懂GPU,最重要是懂渲染管线(或者叫流水线);
而渲染管线,最重要的环节就是shader,即着色器。
所以本文尝试总结GPU的渲染流程和shader,可作为图像开发的入门教程。
2 什么是渲染管线
管线,又称流水线。
什么是流水线呢?
流水线是指在重复执行一项任务时,把它细分成很多小任务,让这些小任务重叠执行,来提高整体的运行效率。
举个栗子:
卸货搬运工,3个人从车上搬到店里。3个人分别是A, B, C。
A给B,B给C,C到店里。
A不需要等C放到店里,再开始下一次的搬运,而是C在搬的过程中,就可以开始搬第二个货物了。
CPU的处理,其实也是用流水线技术,它把一条指令的执行,拆分成五个部分:取指令、解码、取数据,运算和写结果。然后流程跟上面的搬运工差不多。
而渲染管线,就是根据一个三维场景中的顶点、纹理等信息,转换成一张二维图像。这个工作由CPU + GPU 共同完成。
通常把一个渲染流程分3个阶段:
(1) 应用阶段
(2) 几何阶段
(3) 光栅化阶段
应用阶段由CPU完成,几何阶段 和 光栅化阶段 由GPU完成。
当然了,既然是流水线,意味着3个阶段的执行是异步的。也就是,CPU执行完了,不需要GPU执行完才开始下一次调用。
另外,GPU执行的几何阶段和光栅化阶段,也细分了子任务,也是使用流水线的技术。
下面根据这3个阶段,分别讨论一下。
3 CPU处理 ---- 应用阶段
主要工作:
(1) 把数据加载到显存(GPU的内存)
(2) 设置渲染状态
(3) 调用Draw Call
3.1 把数据加载到显存
GPU一般不能直接访问内存,所以自己就搞了个内存,叫显存(显卡内存)。CPU把一些渲染所需数据从硬盘或网络加载到内存,然后送到显存。
数据最主要就两个,模型数据(顶点坐标+纹理坐标)和纹理图像。其他的数据量都很小,如法线方向。加载到显存后,在CPU的内存中的数据,可以删除,例如用bitmap生成一个纹理,加载到GPU后就可以回收了。
3.1.1 加载模型数据例子
下面用一个android视频播放渲染的例子,来说明如何加载模型数据。
视频是在一个二维的矩形框内显示,所以只需要4个顶点坐标,以及对应的4个纹理坐标。纹理用的是视频解码后的图像。
//顶点数据
private float[] vertexData = {
-1f, -1f,
1f, -1f,
-1f, 1f,
1f, 1f
};
//纹理坐标数据
private float[] fragmentData = {
0f, 0f,
1f, 0,
0f, 1f,
1f, 1f
};
public void onCreate() {
//顶点坐标数据在JVM的内存,复制到系统内存
vertexBuffer = ByteBuffer.allocateDirect(vertexData.length * 4)
.order(ByteOrder.nativeOrder())
.asFloatBuffer()
.put(vertexData);
vertexBuffer.position(0);
//纹理坐标数据在JVM的内存,复制到系统内存
fragmentBuffer = ByteBuffer.allocateDirect(fragmentData.length * 4)
.order(ByteOrder.nativeOrder())
.asFloatBuffer()
.put(fragmentData);
//VBO全名顶点缓冲对象(Vertex Buffer Object),他主要的作用就是可以一次性的发送一大批顶点数据到显卡上
int [] vbos = new int[1];
GLES20.glGenBuffers(1, vbos, 0);
vboId = vbos[0];
//下面四句代码,把内存的数据复制到显存中
GLES20.glBindBuffer(GLES20.GL_ARRAY_BUFFER, vboId);
GLES20.glBufferData(GLES20.GL_ARRAY_BUFFER, vertexData.length * 4 + fragmentData.length * 4, null, GLES20. GL_STATIC_DRAW);
GLES20.glBufferSubData(GLES20.GL_ARRAY_BUFFER, 0, vertexData.length * 4, vertexBuffer);
GLES20.glBufferSubData(GLES20.GL_ARRAY_BUFFER, vertexData.length * 4, fragmentData.length * 4, fragmentBuffer);
}
代码中已经加了注释,不过这里还是可以再说明一下。
vertexData 毕竟是java定义的变量,使用的JAVA虚拟机的内存,而不是系统内存,没办法直接给GPU的。所以,先用ByteBuffer,把vertexData拷贝到系统内存。
接着,创建一个顶点缓冲对象(Vertex Buffer Object),他主要的作用就是可以一次性的发送一大批顶点数据到显卡上。然后,调用glBufferData,把数据拷贝到显卡内存上!这样后面GPU开始工作时,就可以快速访问了。
3.1.2 加载纹理的例子
这里再贴一个android app加载纹理图像的例子:
public static int createTexture(Bitmap bitmap){
int[] texture=new int[1];
//生成纹理
GLES20.glGenTextures(1,texture,0);
//生成纹理
GLES20.glBindTexture(GLES20.GL_TEXTURE_2D,texture[0]);
//设置缩小过滤为使用纹理中坐标最接近的一个像素的颜色作为需要绘制的像素颜色
GLES20.glTexParameterf(GLES20.GL_TEXTURE_2D, GLES20.GL_TEXTURE_MIN_FILTER,GLES20.GL_NEAREST);
//设置放大过滤为使用纹理中坐标最接近的若干个颜色,通过加权平均算法得到需要绘制的像素颜色
GLES20.glTexParameterf(GLES20.GL_TEXTURE_2D,GLES20.GL_TEXTURE_MAG_FILTER,GLES20.GL_LINEAR);
//设置环绕方向S,截取纹理坐标到[1/2n,1-1/2n]。将导致永远不会与border融合
GLES20.glTexParameterf(GLES20.GL_TEXTURE_2D, GLES20.GL_TEXTURE_WRAP_S,GLES20.GL_CLAMP_TO_EDGE);
//设置环绕方向T,截取纹理坐标到[1/2n,1-1/2n]。将导致永远不会与border融合
GLES20.glTexParameterf(GLES20.GL_TEXTURE_2D, GLES20.GL_TEXTURE_WRAP_T,GLES20.GL_CLAMP_TO_EDGE);
if(bitmap!=null&&!bitmap.isRecycled()){
//根据以上指定的参数,生成一个2D纹理,上传到GPU
GLUtils.texImage2D(GLES20.GL_TEXTURE_2D, 0, bitmap, 0);
}
return texture[0];
}
先用glGenTextures生成一个纹理id。这时候,还没有创建实际数据。
接着,设置一下纹理的属性,然后,调用texImage2D,这会先创建一个纹理buffer,然后把bitmap拷贝到buffer上。然后完事。上面的函数结束后,bitmap的内容就拷贝到GPU了,可以根据需要回收。
需要强调的是,不管是加载顶点还是纹理,都只需要在初始化时,一次性完成,不需要每次onDraw都加载,否则就没有意义了。
3.2 设置渲染状态
即声明场景的网格(模型)如何被渲染,比如用哪个vertex shader/fragment shader,光源属性,材质(纹理)等。如果绘制不同的网格时没有切换渲染状态,那么前后的网格,将使用同一种渲染状态。
3.3 调用Draw Call
其实就是一个命令,发起方是CPU,接收方是GPU。
当一个Draw Call调用时,GPU就会根据渲染状态(材质,纹理,着色器)和所有的顶点数据进行计算,GPU流水线开始运转,最终生成屏幕显示的像素。
3.4 小结
第一步只需要1次加载就够了,不用每次绘制都加载。 第二和第三,需要每次onDraw时设置。
这里也用绘制视频或图片的onDraw函数,来举个栗子:
public void onDraw(int textureId)
{
GLES20.glClear(GLES20.GL_COLOR_BUFFER_BIT);
GLES20.glClearColor(1f,0f, 0f, 1f);
//设置渲染状态: program根据具体的shader编译,这里就是指定用哪个shader
GLES20.glUseProgram(program);
//设置渲染状态:指定纹理
GLES20.glBindTexture(GLES20.GL_TEXTURE_2D, textureId);
//设置渲染状态:绑定VBO
GLES20.glBindBuffer(GLES20.GL_ARRAY_BUFFER, vboId);
//设置渲染状态:指定顶点坐标在VBO的从0开始,8个数据
GLES20.glEnableVertexAttribArray(vPosition);
GLES20.glVertexAttribPointer(vPosition, 2, GLES20.GL_FLOAT, false, 8,
0);
//设置渲染状态:指定顶点坐标在VBO的从8*4(float是4个字节)开始,8个数据
GLES20.glEnableVertexAttribArray(fPosition);
GLES20.glVertexAttribPointer(fPosition, 2, GLES20.GL_FLOAT, false, 8,
vertexData.length * 4);
//调用Draw Call, GPU 管线开始工作
GLES20.glDrawArrays(GLES20.GL_TRIANGLE_STRIP, 0, 4);
//绘制完成,恢复现场
GLES20.glBindTexture(GLES20.GL_TEXTURE_2D, 0);
GLES20.glBindBuffer(GLES20.GL_ARRAY_BUFFER, 0);
}
4 GPU处理 ----几何阶段
可以把几何阶段和光栅化阶段放在一起,画一张图。
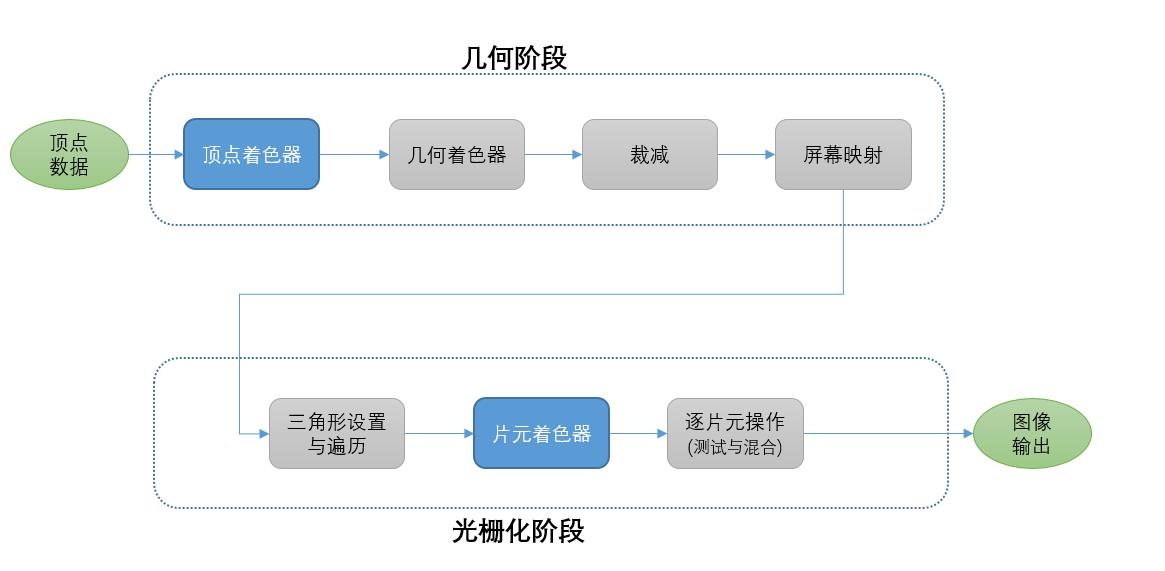
当然了,上图可能不全,中间可能还有些可选的步骤,我只是把最重要的列出来。
其中,蓝色部分的顶点着色器,和片元着色器,是开发者完全可自定义编程的,也是大部分图像开发同学需要关心的2个步骤。
4.1 顶点数据是什么
先来个基本说明:GPU认识的数据,只有点,线,三角形。
这对应1个顶点,2个顶点,3个顶点。这三个又称为图元。点和线一般在2D场景使用,在3D场景,基本是由N多个三角形,来拼接成一个物体模型。
下图是一个人物模型的例子:

放大一些细节,发现都是三角形组合而成。而三角形的顶点,就是我们说的顶点坐标。

所有的三角形贴上二维图片纹理后,就是一个完整的图像:

所以说,顶点数据,一般会包含顶点坐标 + 纹理坐标。
一个模型文件,一般会包含顶点坐标,纹理坐标,纹理本身(纹理可以有多张)等。举个栗子,打开3D max的obj后缀的模型文件,就可以看到如下文本内容:
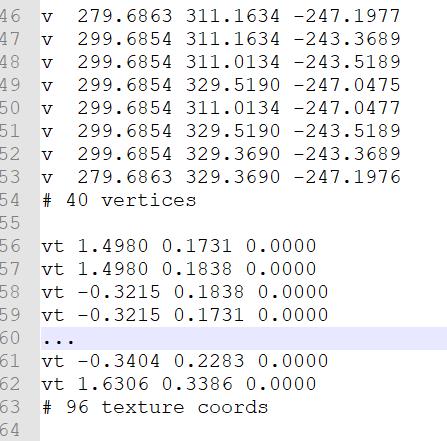
4.2 顶点着色器
顶点着色器是GPU内部流水线的第一步。
它的处理单位是顶点,也就是每个顶点,都会调用一次顶点着色器。
它的主要工作:坐标转换和逐顶点光照,以及准备后续阶段(如片元着色器)的数据。
坐标转换,即把顶点坐标从模型坐标空间转换到齐次裁切坐标空间。
这里给一个Unity的shader代码,Unity把顶点着色器和片元着色器的代码,放到了一个文件中,不过Unity引擎会解析文件,转换2个着色器代码段,传递给GPU。
Shader "Unlit/SimpleUnlitTexturedShader"
{
Properties
{
// 我们已删除对纹理平铺/偏移的支持,
// 因此请让它们不要显示在材质检视面板中
[NoScaleOffset] _MainTex ("Texture", 2D) = "white" {}
}
SubShader
{
Pass
{
CGPROGRAM
// 使用 "vert" 函数作为顶点着色器
#pragma vertex vert
// 使用 "frag" 函数作为像素(片元)着色器
#pragma fragment frag
// 顶点着色器输入
struct appdata
{
float4 vertex : POSITION; // 顶点位置
float2 uv : TEXCOORD0; // 纹理坐标
};
// 顶点着色器输出("顶点到片元")
struct v2f
{
float2 uv : TEXCOORD0; // 纹理坐标
float4 vertex : SV_POSITION; // 裁剪空间位置
};
// 顶点着色器
v2f vert (appdata v)
{
v2f o;
// 将位置转换为裁剪空间
//(乘以模型*视图*投影矩阵)
o.vertex = mul(UNITY_MATRIX_MVP, v.vertex);
// 仅传递纹理坐标
o.uv = v.uv;
return o;
}
// 我们将进行采样的纹理
sampler2D _MainTex;
// 像素着色器;返回低精度("fixed4" 类型)
// 颜色("SV_Target" 语义)
fixed4 frag (v2f i) : SV_Target
{
// 对纹理进行采样并将其返回
fixed4 col = tex2D(_MainTex, i.uv);
return col;
}
ENDCG
}
}
}
代码已经加了清晰的注释。
appdata就是顶点着色器的输入,包括顶点坐标和纹理坐标。
通常,顶点着色器只处理顶点坐标,进行空间转换。 纹理坐标,一般透传给片元着色器。
空间转换代码竟然及其简单,就是坐标乘于一个MVP矩阵!
接下来,我们就基于MVP矩阵,来展开说一下空间转换的概念。
4.3 坐标空间
什么是坐标空间呢?其实他在我们生活中处处存在。例如,你跟朋友约定在博物馆大门右转100米处见面,这时候,你说的位置,是一个以博物馆的大门为原点的空间。所以坐标空间,是一个相对的概念。
在游戏世界中也一样。
根据不同的参照物,可以分为模型空间-世界空间-观察空间-裁剪空间-屏幕空间。
在3D世界中,顶点坐标有3个数据,是(x, y, z),但为了方便做平移/旋转/缩放等转换,需要补充一个w分量。即(x, y, z, w),把这个4维的坐标,称为齐次坐标。这些知识,见第五节的附录知识。
接下来,我们来挨个讨论这些空间。
4.3.1 模型空间
你在3D max制作了一个人物模型,该模型可以放到各种软件中适配。 对模型内部来说,有一个坐标原点,比如就在心脏处,那身体各个部位相对于心脏,就有一个坐标值;
每个模型对象,都有自己独立的坐标空间。所以也可以称为对象空间或局部空间。
4.3.2 世界空间
可以把游戏中的一个地图,作为一个小小的世界,地图的中心,可以作为坐标原点。人物模型作为一个整体,放到地图中,就有了相对地图中心的一个坐标值。这就是世界空间。
把模型空间的坐标,转换到世界空间的坐标,可以通过矩阵运算得到。这个矩阵叫Model Matrix。
事实上,一个模型放到地图中,可能会先缩放,然后旋转或者平移。这3者都有对应的矩阵,具体见附录。
换言之,这个矩阵是由物体在地图中的缩放,旋转,平移参数决定的。
换算的目的,就是得到物体的某个顶点,在地图中是个什么具体位置。
4.3.3 观察空间
也可以称为摄像机空间。观察空间指的是,游戏地图那么大,我们只能看到一部分内容。于是在游戏地图中,定义一个Camera,它也处于世界空间中。camera就相当于我们的眼睛,camera照到哪里,哪里就是我们看到的画面。
在3D游戏中,经常就把Camera和用户角色绑在一起。角色对象走到哪,Camera对象就移动到哪,效果便是,走到哪,就看到哪里的风景!
所以地图中的任何物体,如果把Camera作为坐标原点,也有一个相对于Camera的坐标值。以Camera为原点的空间,就是观察空间了。
把世界空间的坐标,换算到观察空间,也可以通过矩阵运算得到。这个矩阵叫View Matrix。
这个矩阵依赖什么参数呢?
首先,摄像机本身也位于世界坐标系中,如果不考虑摄像机往哪里看,那其实就是很简单的平移矩阵。
即,摄像机A坐标如果是(-3, 0, 0), 那摄像机就是从世界原点O平移(-3, 0, 0)的结果。如果把摄像机的坐标作为新的原点,那原来的世界原点O,相当于从摄像机平移(3, 0, 0)的结果。所以两个坐标系的转换矩阵,近乎是一个平移矩阵。
当然了,实际摄像机还有朝向,以及眼睛是正面看,还是倒立看。不知道啥是倒立看?看下图

所以这个矩阵总用有三个因素影响。
来,一个函数解决烦恼,忘记复杂的计算过程。
glm::mat4 CameraMatrix = glm::LookAt(
cameraPosition, // the position of your camera, in world space
cameraTarget, // where you want to look at, in world space
upVector // probably glm::vec3(0,1,0), but (0,-1,0) would make you looking upside-down, which can be great too
);
4.3.4 裁减空间
裁减空间就是摄像机能看到的区域。这个区域成为视椎体。
它由6个平面组成,这些平面也成为裁减平面。视椎体有两种类型,涉及两种投影方式。一个是透视投影,一个是正交投影。
完全位于这块空间的图元,会被保留;
完全位于空间之外的图元,完全丢弃;
和空间边界相交的图元,会被裁减。
下图是一个透视投影的示意图。人物完全在视椎体内,所以右下角的小图,是最终用户看到的2D画面样子。
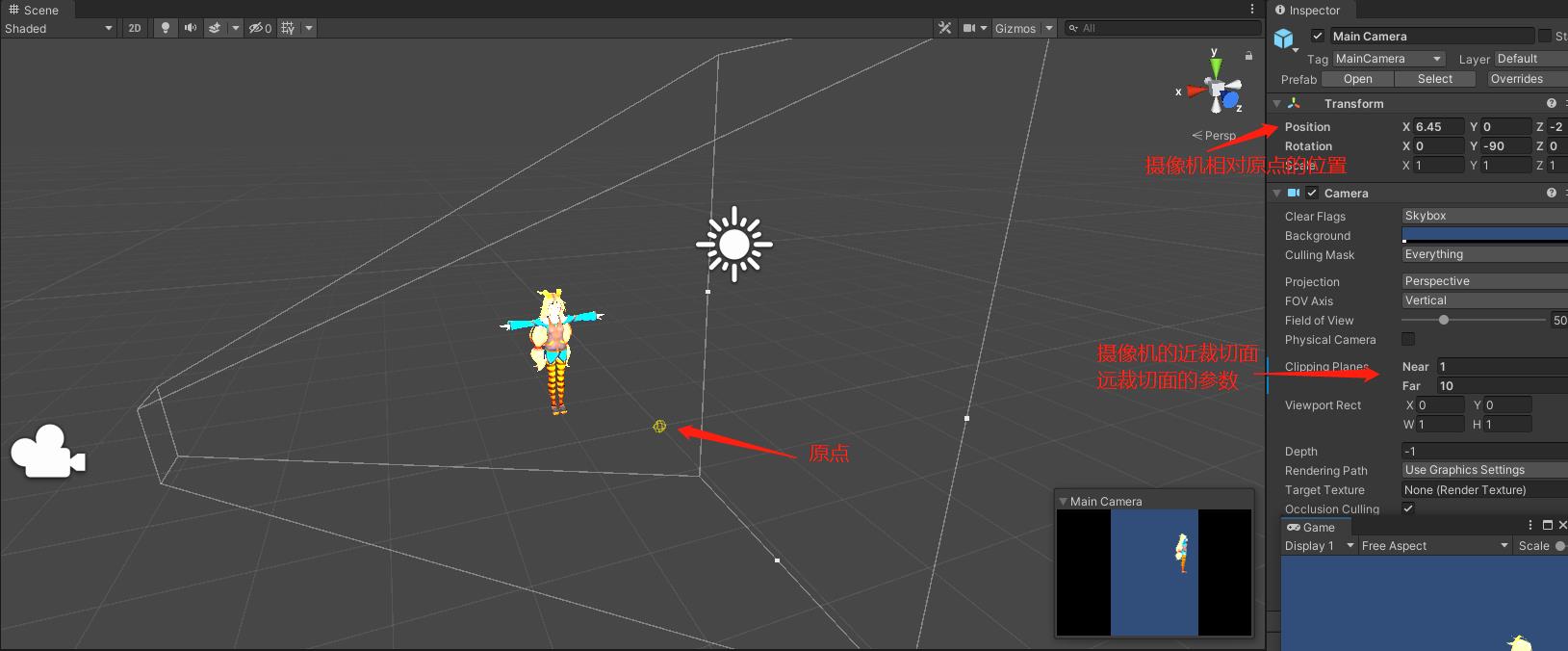
当然了,图中的Near 和Far,我是为了显示方便,设置了比较小的值。实际游戏中,Near和Far差别很大,比如Near = 0.1, Far = 1000。这跟人眼可看的范围是差不多的,近到贴眼睛的东西看不见,非常远的东西,也看不见。
那么,如何判断一个东西就在视椎体内呢?
答案是通过一个投影矩阵,把顶点转换到一个裁减空间。
这个矩阵,基本上由摄像机的参数决定。
参数示意图如下:
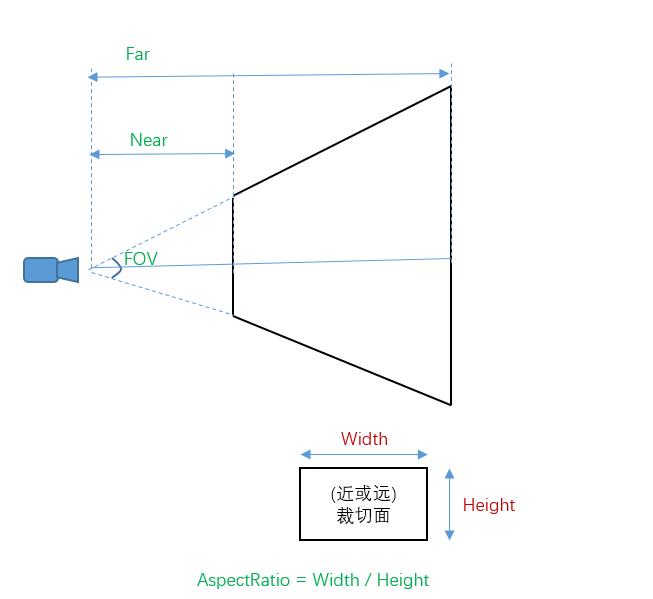
FOV代表视角的度数(Field of View);
Near和Far是摄像机原点,距离裁切面的距离;
AspectRatio是裁切面的宽高比;
从观察空间到裁减空间的变化矩阵,咱成为Projection Matrix。
矩阵可以用一个函数来生成:
// Generates a really hard-to-read matrix, but a normal, standard 4x4 matrix nonetheless
glm::mat4 projectionMatrix = glm::perspective(
glm::radians(FoV), // The vertical Field of View, in radians: the amount of "zoom". Think "camera lens". Usually between 90° (extra wide) and 30° (quite zoomed in)
AspectRatio, // Aspect Ratio. Depends on the size of your window. such as 4/3 == 800/600 == 1280/960, sounds familiar
Near, // Near clipping plane. Keep as big as possible, or you'll get precision issues.
Far // Far clipping plane. Keep as little as possible.
);
具体公式生成原理,这里就不展开了,详情自行google或者看这里:https://zhuanlan.zhihu.com/p/104768669。
投影矩阵虽然有投影两个字,但是没有做真正的投影。而是在做投影的准备工作。 投影要到下一步,到屏幕空间的转换,才使用。
进行投影矩阵运算后,或者说,到了裁剪空间后,w值就不一定是0和1了,有特殊的含义。具体而言,如果一个顶点在视椎体内,那么它变换后的坐标,必须满足:
-w <= x <= w
-w <= y <= w
-w <= z <= w
不符合要求的,要么剔除,要么裁减。
举个例子:
一个人物模型的手的一个顶点坐标,到观察空间的坐标是
【9, 8.81, -27.31, 1】
经过换算到裁减空间,值是
【11.691, 15.311, 23.69, 27.3】
那么,该顶点是在裁减空间内,可以被显示。
前面都是以透视投影来说明的。那么,正交投影跟透视投影啥区别呢?
透视投影:越远的东西,呈现在屏幕的越小; 正交投影,远和近的同样大小东西,呈现在屏幕上一样大。
来一张亲手绘制的图,你就知道我的意思了!
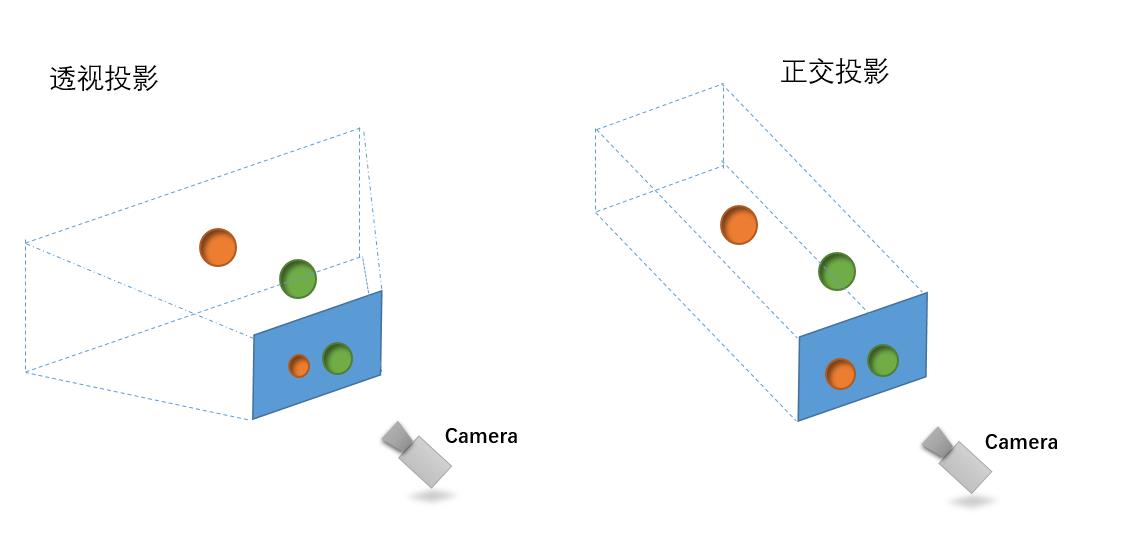
从上面可知,透视投影更有3D效果,正交透明则没有,比较适合2D游戏。
4.3.5 屏幕空间
屏幕空间是一个二维空间了。也是我们将要看到的画面,也是最后一个需要知道的空间了(是不是长吁一口气,哈哈)
要把顶点从裁减空间转换到屏幕空间,三维变二维了,所以所叫投影。
这个投影主要做两件事:
第一,需要进行齐次除法。不要觉得复杂,其实就是用w分量去处于x, y, z分量。在Open GL中,把这一步得到的坐标,叫做归一化的设备坐标(Normalized Device Coordinates, NDC)。
NDC的x, y, z的有效值范围,都是负1到1。在这个值之外的,就是被剔除的点。
第二,需要映射到屏幕,得到屏幕坐标。在openGL中,屏幕的左下角的像素坐标是(0, 0),右上角是(pixelWidth, pixelHeight)。
比如归一化坐标是(x, y),屏幕宽高是(w,h),那么,屏幕坐标是
Sx = x*w + w/2
Sy = y*h + h/2
你是不是想说,NDC的z分量不要了?
不会不会, z分量也有很大的价值,它作为深度缓冲。比如,如果之后有2个顶点,屏幕坐标都一样,且都不透明,那就看深度缓冲了,谁离摄像头近,谁就显示。
需要强调的是,从裁减空间到屏幕空间的转换,是由底层帮我们完成的,不需要代码实现。
顶点着色器,只需要把顶点,从模型空间转换到裁减空间即可。
在片元着色器,可以得到该片元在屏幕空间的位置。
4.4 顶点坐标变换总结
回到4.2节,我们说了一个MVP矩阵,现在终于知道了,它代表了一个可以把顶点从模型空间转换到裁减空间的矩阵!
这个矩阵,又是由 模型矩阵 * 观察矩阵 * 投影矩阵相乘得到的!
用一张图来说明一下:
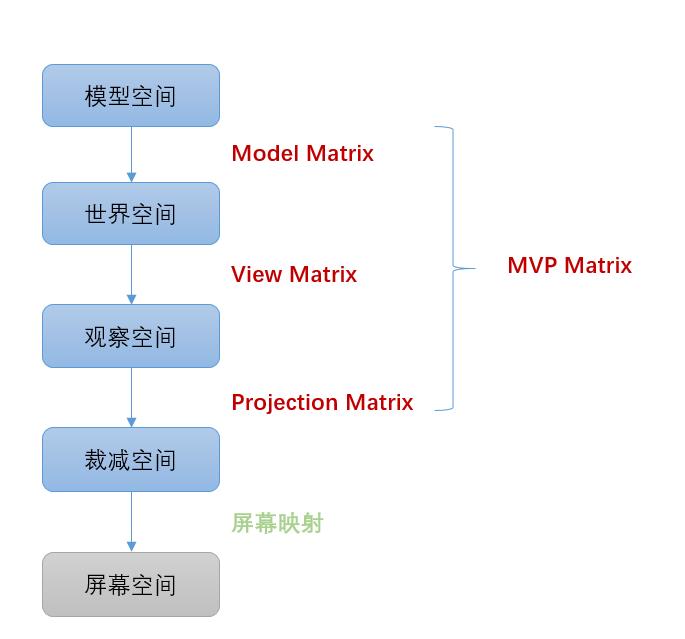
这和4.2节的这段代码,终于对上了:
o.vertex = mul(UNITY_MATRIX_MVP, v.vertex);
这个宏UNITY_MATRIX_MVP,就是图中的MVP矩阵。
当你确定了模型位置/旋转/缩放,就有了Model Matrix。当确定了摄像机位置,朝向,就有了View Matrix。当确定了摄像机的FOV视角,近远裁切面的距离等,就有了Projection Matrix。
三者都确定了,相乘,MVP Matrix也就确定了。
所以顶点着色器非常的简单,乘于一个固定MVP矩阵就OK了!
咱们再往回看3.1节,那是一个视频播放的例子,顶点坐标用了:
private float[] vertexData = {
-1f, -1f,
1f, -1f,
-1f, 1f,
1f, 1f
};
为什么这么简单?因为它仅用于视频播放,画面是矩形。只需要4个顶点,顶点坐标就是二维的。
所以,这里的顶点,直接写成了裁减空间下的值(z没写默认为0)。
这种情况下,MVP矩阵是一个单位矩阵。
来看一下3.1节对应的顶点着色器代码,也是简单到令人发指:
attribute vec4 v_Position;
attribute vec4 f_Position;
varying vec2 textureCoordinate;
void main()
{
gl_Position = v_Position;
textureCoordinate = f_Position.xy;
}
注意,这个和4.2节不太一样,这一段已经是可以直接给openGL编译的shader,4.2节是unity封装的代码形式,最后Unity的引擎,也会翻译成类似上面的代码,有main函数。
v_Position是外部输入的顶点坐标,gl_Position是全局内建变量,代表最后在裁减空间下的坐标。
如果上面的shader非要写MVP,也是可以的,只不过,这个MVP是一个单位矩阵。
即
gl_Position = mvpMatrix * v_Position;
5 GPU处理 ---- 光栅化阶段
光栅化的主要任务:计算每个图元都覆盖了哪些像素,然后给这些像素着色。
5.1 三角形设置与遍历
三角形设置:
这是光栅化流水线的第一个阶段。
这个阶段会计算光栅化一个三角网格所需的信息。
具体而言,上一个阶段输出的,都是在屏幕上的二维的三角网格的顶点。即我们得到的是三角网格每条边的两个端点。但如果要得到整个三角网格对像素的覆盖情况,我们就必须计算每条边上的像素坐标。为了能够计算边界像素的坐标信息,我们就需要得到三角形边界的表示方式。这样一个计算三角网格表示数据的过程就叫做三角形设置。它的输出是为了给下一个阶段做准备。
三角形遍历:
三角形遍阶段将会检查每个像素是否被一个三角网格所覆盖。如果被覆盖的话,就会生成一个片元,而这样一个找到哪些像素被三角网格覆盖的过程就是三角形遍历。三角形遍历阶段会根据上一个阶段的计算结果来判断一个三角网格覆盖了哪些像素,并使用三角网格3个顶点的顶点信息对整个覆盖区域的像素进行插值。下图展示了三角形遍历阶段的简化计算过程。
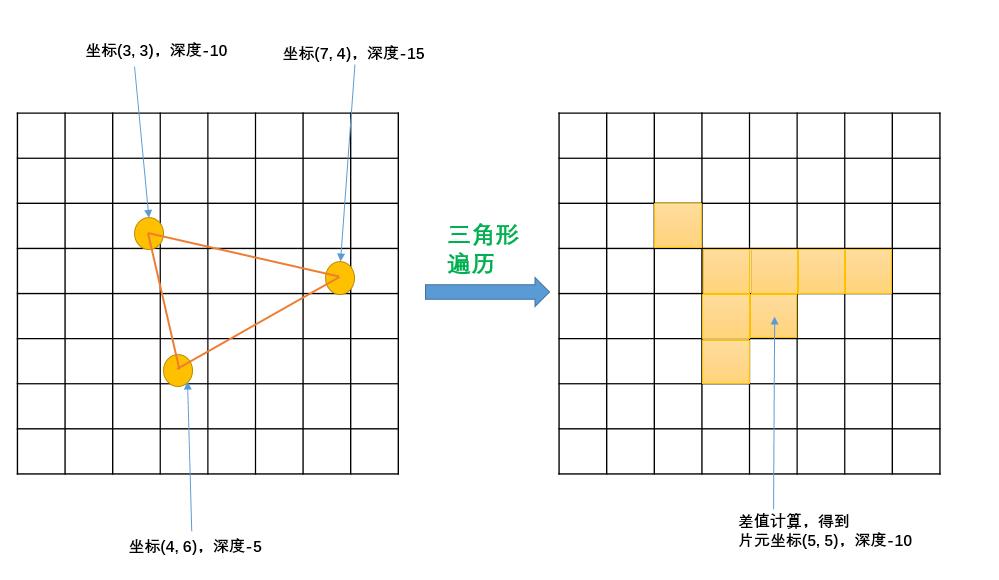
根据几何阶段输出的顶点信息,得到三角网格覆盖的像素位置。对应的像素会生成一个片元,片元中的状态,由三角形的顶点信息,进行差值计算得到。
像上图的三角网格,共产生了8个片元。
5.2 片元着色器
6 附录知识
6.1 什么是齐次坐标
齐次坐标就是用N+1维来代表N维坐标。
例如笛卡尔坐标系的坐标(x, y, z),用(x, y, z, w)来表示。坐标可以是点,或向量。
目的:
区分向量或者点。辅助 平移T、旋转R、缩放S这3个最常见的仿射变换
引经据典:
齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射几何变换。
—— F.S. Hill, JR 《计算机图形学 (OpenGL 版)》作者
关于区分向量和点,指的是:
(1) 从普通坐标转换成齐次坐标时
如果(x,y,z)是个点,则变为(x,y,z,1);
如果(x,y,z)是个向量,则变为(x,y,z,0)
(2) 从齐次坐标转换成普通坐标时
如果是(x,y,z,1),则知道它是个点,变成(x,y,z);
如果是(x,y,z,0),则知道它是个向量,仍然变成(x,y,z)
关于平移,旋转,缩放,且慢慢道来。
6.2 平移矩阵
平移矩阵是最简单的变换矩阵。平移矩阵是这样的:
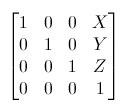
其中,X、Y、Z是点的位移增量。
例如,若想把向量(10, 10, 10, 1)沿X轴方向平移10个单位,可得:
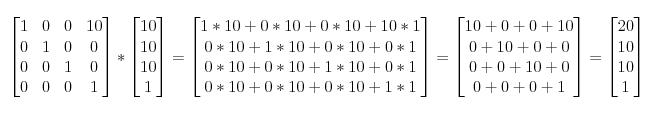
看到没,如果平移要用矩阵来运算,矩阵必须是4x4的,那点(10, 10, 10)只能增加一维w,才能被计算(矩阵乘法的要求,mn的矩阵,只能乘于nt 的矩阵)。
6.3 缩放矩阵
缩放也很简单

例如把一个向量(点或方向皆可)沿各方向放大2倍:
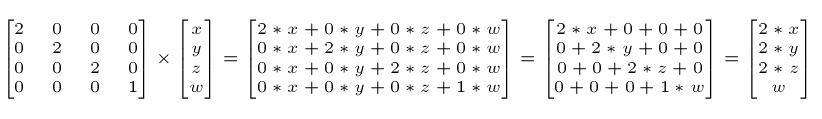
6.4 旋转矩阵
这个稍微复杂一些,沿着X, Y, Z轴的旋转不一样,不过最后还是一个矩阵。这里不再单独展开。有兴趣可以参考:
6.5 组合变换
上面介绍了旋转、平移和缩放的运算方法。把这些矩阵相乘就能将它们组合起来,例如:
TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;
注意,是先执行缩放,接着旋转,最后才是平移。这就是矩阵乘法的工作方式,也是我们对3D模型放到地图中的常用操作方式。
3个矩阵相乘,还是一个矩阵,这就是组合变换的矩阵,所以最后也可以写成:
TransformedVector = TRSMatrix * OriginalVector;
参考
Android OpenGL ES 1.基础概念
计算机组成原理–GPU
计算机那些事(8)——图形图像渲染原理
opengl-tutorial
Unity文档
光栅化阶段设置
以上是关于GPU 渲染管线与着色器 大白话总结 ---- 一篇就够的主要内容,如果未能解决你的问题,请参考以下文章