MATLAB应用实战系列（七十）-非线性可视化-非线性相图&混沌系统

Posted 2021-10-29 文宇肃然

前言

以下是我为大家准备的几个精品专栏，喜欢的小伙伴可自行订阅，你的支持就是我不断更新的动力哟！

MATLAB-30天带你从入门到精通

MATLAB深入理解高级教程（附源码）

tableau可视化数据分析高级教程

python快速学习实战应用系列课程

非线性相图

我们用几个例子，来介绍非线性系统的相图的绘制方法。

这里举的例子都是自治系统方程的例子，也就是方程结果与t0的初始取值无关（时不变系统），不含外部周期性驱动力之类的与t相关的量。因为描述自治系统，只需要知道系统的空间上的各个变量的导数，然后组成相空间即可。而时变系统各个状态都会随时间变化，无法用静态的相图去定性分析。

所以对于自治二阶系统，二阶的相平面已经可以完全的描述出系统的运动状态，无论线性还是非线性。通常的步骤可以分为两步：（1）计算出每一个点的dy和ddy导数，（2）根据每个点得到的向量，绘制出向量场对应的流线图。

以《非线性系统》这本书中给出的一个例子作为展示。其中二阶非线性方程的公式如下：

绘制出空间中每一个点的系统导数，绘制出流线，即可得到这个非线性系统的相图。

可以看到，非线性系统的相平面，可能拥有不止一个平衡点。但是这些平衡点附近的邻域，也都可以线性化，用上一节中的线性系统的相图来解释其行为。比如上图，就拥有两个稳定结点，和一个鞍点。

接下来再介绍一种只有在非线性条件下，才会出现的一种经典相平面图案：极限环。

以经典的Van der Pol方程为例，这个方程的形式如下：

后面的ε为一个常数，ε越大方程的非线性越大。取ε=0.3，绘制出相空间图：

整个空间只有一个平衡点，即极限环内部发散的螺旋点。为了直观的了解极限环的特性，选取不同的初始条件，对方程进行时域的求解，得到下面的结果：

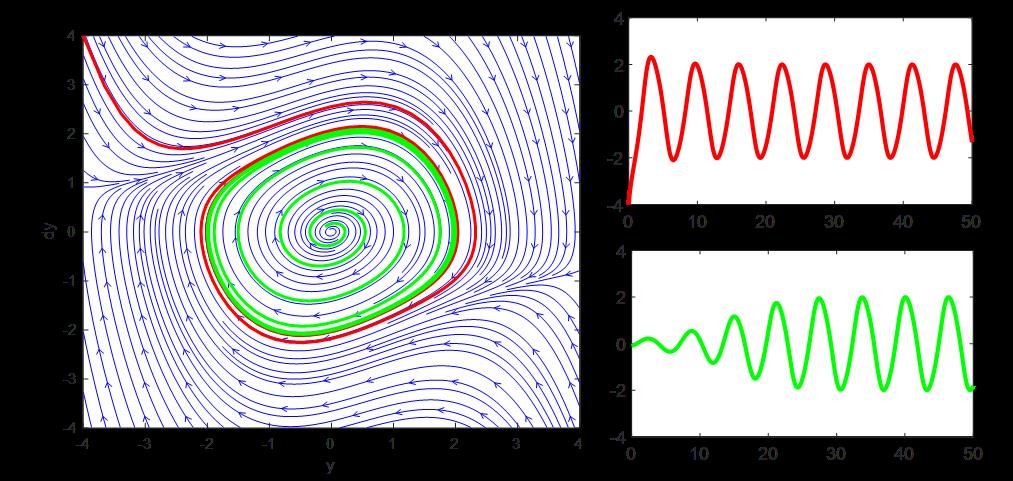
在极限环外的点，刚开始呈现出收敛的波形，但是随后振幅保持恒定。在极限环里面的点，刚开始呈现出发散的波形，但是随后振幅也保持稳定。两者都被空间中的极限环所吸引，进行周而复始的画圈圈运动中。

如果方程中某些系数发生变化（比如上面方程的ε由负变为正），会导致整个相空间发生改变。这种改变会使得平衡点性质发生变化，导致整个系统的性质发生变化，我们称系统在这个位置发生了分岔。比如Van der Pol方程的ε由负变为正，平衡点由稳定变为发散，导致空间中稳定位置由一个点变为一个运动的极限环。

如果实验中能够观测到振动信号，也可以用绘制相平面的方法，观测信号的特性。下面用三幅图给出了测量过程中常见周期信号的相平面图：

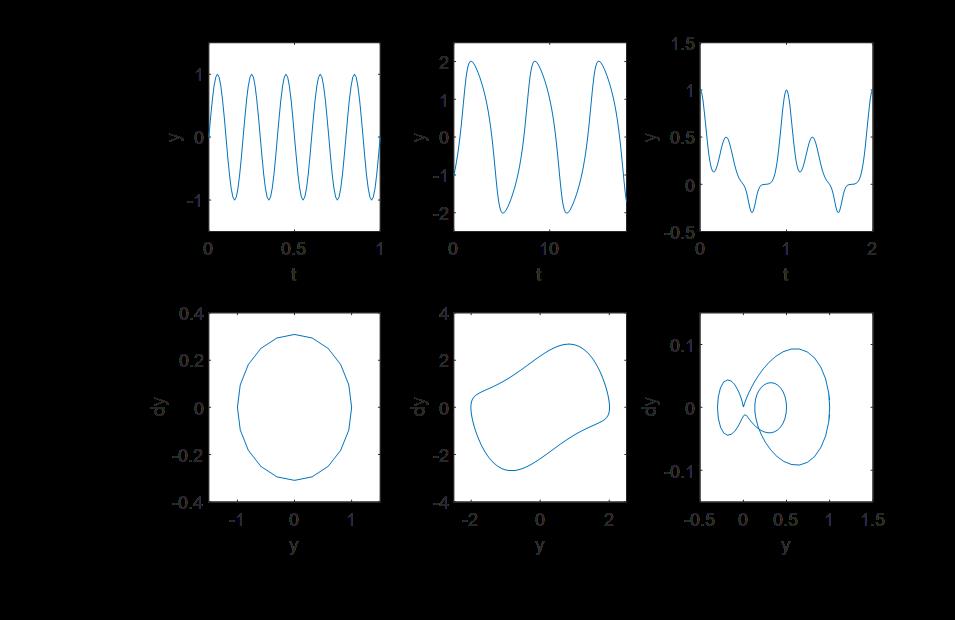
第一幅图为典型的线性振动图，波形为正弦曲线，相平面为一个圆。

第二幅图为典型的极限环振动。这类振动有个特点，就是即使受到扰动，振幅也能始终保持在一个稳定的值。在实际实验中如果发现这个现象，而且没有外部周期驱动力（方程为自治系统），则基本能确定其为极限环运动。

第三幅图为典型的高维非线性。因为相平面内的流线不会交叉。这种交叉曲线是高维空间在二维平面上的投影。图中展示的是高维非线性中的倍周期现象的模拟。这个在后面文章中会介绍到。

当然，实际试验中由于噪声，测量的结果不会这么好看。比如最终的结果如果杂乱无章没有规律，理论上肯定是混沌现象出现了，但实际上很有可能是噪声太大而已。

后面附上绘图用到的matlab代码：

%1二维相空间%非线性clearclcclose all
%1多平衡点的非线性系统%参考 非线性系统（中文翻译第三版） Khalil P32[y,dy]=meshgrid(-0.5:0.02:1.5,-0.5:0.02:1.5);%初始化网格u=zeros(size(y));v=u;for k=1:numel(y)    %计算网格上每一个点的上的方向    F=Fdydx(0,[y(k);dy(k)],1);    u(k)=F(1);    v(k)=F(2);endfigure()streamslice(y,dy,u,v,4)xlabel('y')ylabel('dy')box on
%2极限环[y,dy]=meshgrid(-4:0.1:4,-4:0.1:4);%初始化网格u=zeros(size(y));v=u;for k=1:numel(y)    %计算网格上每一个点的上的方向    F=Fdydx(0,[y(k);dy(k)],2);    u(k)=F(1);    v(k)=F(2);endfigure()streamslice(y,dy,u,v,3)xlabel('y')ylabel('dy')box onxlim([-4,4]);ylim([-4,4])
figure()streamslice(y,dy,u,v,3)xlabel('y')ylabel('dy')box onhold ont2=0:0.1:50;[y2,~]=ODE_RK4_hyh(t2,t2(2)-t2(1),[-4;4],2);plot(y2(1,:),y2(2,:),'r','linewidth',2)[y3,~]=ODE_RK4_hyh(t2,t2(2)-t2(1),[-0.1;0.1],2);plot(y3(1,:),y3(2,:),'g','linewidth',2)hold offxlim([-4,4]);ylim([-4,4])figure()plot(t2,y2(1,:),'r','linewidth',2);ylim([-4,4])figure()plot(t2,y3(1,:),'g','linewidth',2);ylim([-4,4])
%3不同时域信号在相图上的样子figure()t1=0:0.01:1;y1=sin(10*pi*t1);dy1=diffhyh(y1,2);subplot(2,3,1)plot(t1,y1);ylim([-1.5,1.5])xlabel('t');ylabel('y')subplot(2,3,4)plot(y1,dy1);xlim([-1.5,1.5])xlabel('y');ylabel('dy')%非线性极限环
t2=0:0.01:18;[y,Output]=ODE_RK4_hyh(t2,t2(2)-t2(1),[-1;1.161],2);y2=y(1,:);dy2=y(2,:);subplot(2,3,2)plot(t2,y2);ylim([-2.5,2.5]);xlim([0,18])xlabel('t');ylabel('y')subplot(2,3,5)plot(y2,dy2);xlim([-2.5,2.5])xlabel('y');ylabel('dy')
%混沌（模拟的信号，并没有给出实际的系统）%二维系统下，相平面是可以完全描述系统的，不可能出现交叉。%如果出现轨线交叉，则说明系统的维度大于2，相平面展示的图形只是高维系统在2维上的投影。t3=0:0.01:2;Gas=@(t,a,b,c) c*exp(-b*(t-a).^2);y3=Gas(t3,0,120,1)+Gas(t3,1,120,1)+Gas(t3,2,120,1);y3=y3+Gas(t3,0.3,90,0.5)+Gas(t3,1.3,90,0.5);y3=y3-Gas(t3,0.6,300,0.3)-Gas(t3,1.6,300,0.3);dy3=diffhyh(y3,2);subplot(2,3,3)plot(t3,y3);ylim([-0.5,1.5])xlabel('t');ylabel('y')subplot(2,3,6)plot(y3,dy3);xlim([-0.5,1.5]);ylim([-0.15,0.15])xlabel('y');ylabel('dy')
function [F,Output]=Fdydx(x,y,Input)%形式为Y'=F(x,Y)的方程，参见数值分析求解常系数微分方程相关知识%高次用列向量表示，F=[dy(1);dy(2)];y(1)为函数，y(2)为函数导数switch Input    %示例1    case 1        p=[83.72,-226.31,229.62,-103.79,17.76,0];        dy(1)=0.5*(-polyval(p,y(1))+y(2));        dy(2)=0.2*(-y(1)-1.5*y(2)+1.2);        F=[dy(1);dy(2)];    %示例2    case 2        dy(1)=y(2);        dy(2)=-y(1)+0.3*(1-y(1)^2)*y(2);%0.3        F=[dy(1);dy(2)];endOutput=[];end
function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)%4阶RK方法%h间隔为常数的算法y=zeros(size(y0,1),size(x,2));y(:,1)=y0;for ii=1:length(x)-1    yn=y(:,ii);    xn=x(ii);    [K1,~]=Fdydx(xn    ,yn       ,Input);    [K2,~]=Fdydx(xn+h/2,yn+h/2*K1,Input);    [K3,~]=Fdydx(xn+h/2,yn+h/2*K2,Input);    [K4,~]=Fdydx(xn+h  ,yn+h*K3  ,Input);    y(:,ii+1)=yn+h/6*(K1+2*K2+2*K3+K4);endOutput=[];end
function Fdiff=diffhyh(F,dim)%采用2阶中心差分，边缘采用一阶向前或向后差分（边缘没有搞迎风差分，精度要求不高）%dim，差分的维度方向，dim=1对应着矩阵向下方向的差分，dim=2对应的向右diffF1=diff(F,1,dim);if dim==1%向下    Fdiff=([zeros(1,size(F,2));diffF1]+[diffF1;zeros(1,size(F,2))])/2;    Fdiff(1,:)=diffF1(1,:);    Fdiff(end,:)=diffF1(end,:);elseif dim==2%向右    Fdiff=([zeros(size(F,1),1),diffF1]+[diffF1,zeros(size(F,1),1)])/2;    Fdiff(:,1)=diffF1(:,1);    Fdiff(:,end)=diffF1(:,end);endend

混沌系统

如果二维相平面中出现了交叉的轨线，则说明这个系统的维度很可能大于二维。

下面就以几个经典的系统作为示范。本章节不涉及太多知识点，以展示为主。主要介绍三个经典的非线性混沌系统。

• 1 Lorenz系统

Lorenz系统是气象学家洛伦兹发现并提出的一个非线性系统，也是混沌学科的开端。在模拟大气流动时，洛伦兹发现初始的一个小小的误差，都会导致系统未来极大的变化。这种思想在20世纪60年代，给了那些物理学界中决定论者沉重的打击。洛伦兹也将这种不确定性，总结为“蝴蝶效应”。

这个系统可以被写为：

一般系统a=10，b=8/3，变化r值来观察系统的不同样子。下图分别展示了取不同r值所对应的xy平面的二维相轨线图：

其中r=20时，对应系统收敛到定点。r=28对应混沌。r=99.36对应倍周期。

因为二维系统在相平面上不会出现交叉，所以混沌、倍周期等现象都是在三维或者更高维才出现。正如前文所说的，对于混沌来说，三是个神奇的数字。

它们在三维空间中的轨迹图为：

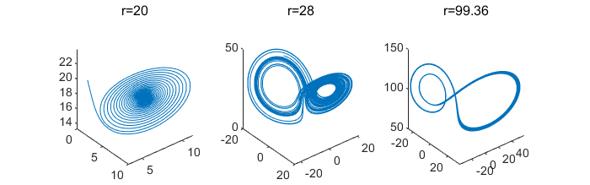
中间的那个图就是经典的洛伦兹吸引子图。

• 2 Rossler系统

Rossler系统是Rössler本人在70年代提出的一个非线性系统，和前面的Lorenz系统相比更为简单，但是却依然拥有复杂的非线性行为。

它可以写作：

下图绘制了a=0.1，b=0.1，改变不同的c绘制的轨迹图。

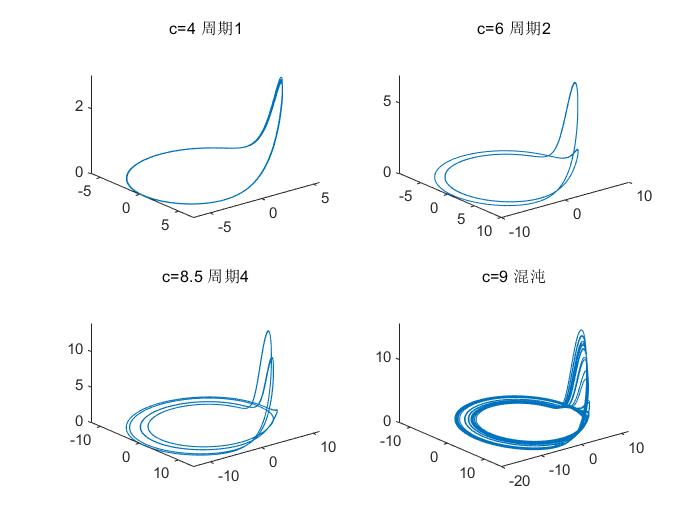
其中周期2指的是每两个波形一个循环，系统转2圈回到同一个点。随着c的增大，系统由周期1到了周期2，之后突然增加大周期4，再之后以越来越快的速度增大到周期8甚至更高，最后密密麻麻的周期似乎再也不会循环，变成了混沌。

这种周期越来越多逐渐变为混沌的现象，叫做倍周期分岔现象。是系统由有序变为无序混沌常见的一种方式。

• 3 duffing方程

duffing方程也是以 Georg Duffing命名的一个非线性方程。它是基于强迫振动的单摆所提出的方程，它提出的时间非常早，但是被拿来做混沌研究还是比较晚的。由于它背后有着非常明显与简单的物理模型，所以甚至可以做实验去观察这个方程的非线性[3]。方程的形式为：

与前面两个方程不同，duffing方程存在一个强迫振动项，带有时间t，所以不属于自治系统。可以看到虽然系统是二阶的，但仍然具有非常复杂的非线性。

如下图，固定激励的振幅频率r和w，改变阻尼d。

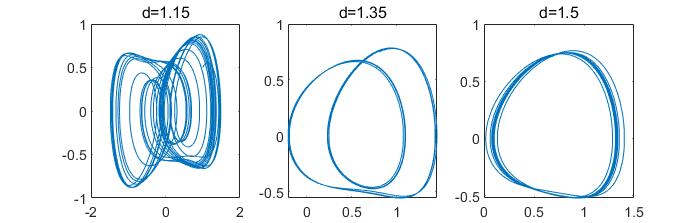
可以看到随着阻尼d的增大，系统由混沌变为2周期，又变为了单周期运动。

对于这种一团乱麻的混沌现象，只观察轨迹图并不能看到什么规律。下一章节我们将引入一种新的观测方法——庞佳莱截面法。

后面附上代码：​​​​​​​

clcclearclose all%% 洛伦兹吸引子h=1e-3;x0=0:h:40;[y1,~]=ODE_RK4_hyh(x0,h,[1;4;20],{'Lorenz',[10,8/3,20]});Lx=y1(1,:);Ly=y1(2,:);Lz=y1(3,:);
figure(1)subplot(1,3,1)plot(Lx,Ly);title('r=20')figure(2)subplot(1,3,1)plot3(Lx,Ly,Lz);view([51,30]);title('r=20')
[y1,~]=ODE_RK4_hyh(x0,h,[-13;-2;41],{'Lorenz',[10,8/3,28]});Lx=y1(1,:);Ly=y1(2,:);Lz=y1(3,:);
figure(1)subplot(1,3,2)plot(Lx,Ly);title('r=28')figure(2)subplot(1,3,2)plot3(Lx,Ly,Lz);view([51,30]);title('r=28')
[y1,~]=ODE_RK4_hyh(x0,h,[1;4;67],{'Lorenz',[10,8/3,99.36]});Lx=y1(1,:);Ly=y1(2,:);Lz=y1(3,:);
figure(1)subplot(1,3,3)plot(Lx,Ly);title('r=99.36')figure(2)subplot(1,3,3)plot3(Lx,Ly,Lz);view([51,30]);title('r=99.36')
%% Rossler吸引子h=2e-3;x0=0:h:180;[y1,~]=ODE_RK4_hyh(x0,h,[4.9;-5;0.07],{'Rossler',[0.1,0.1,4]});Lx=y1(1,:);Ly=y1(2,:);Lz=y1(3,:);
figure(4)subplot(2,2,1)plot3(Lx,Ly,Lz);view([51,30]);title('c=4 周期1')
[y1,~]=ODE_RK4_hyh(x0,h,[9.1;-5;0.17],{'Rossler',[0.1,0.1,6]});Lx=y1(1,:);Ly=y1(2,:);Lz=y1(3,:);
figure(4)subplot(2,2,2)plot3(Lx,Ly,Lz);view([51,30]);title('c=6 周期2')
[y1,~]=ODE_RK4_hyh(x0,h,[12.8;-5;0.277],{'Rossler',[0.1,0.1,8.5]});Lx=y1(1,:);Ly=y1(2,:);Lz=y1(3,:);
figure(4)subplot(2,2,3)plot3(Lx,Ly,Lz);view([51,30]);title('c=8.5 周期4')
[y1,~]=ODE_RK4_hyh(x0,h,[12.8;-5;0.277],{'Rossler',[0.1,0.1,9]});Lx=y1(1,:);Ly=y1(2,:);Lz=y1(3,:);
figure(4)subplot(2,2,4)plot3(Lx,Ly,Lz);view([51,30]);title('c=9 混沌')
%% Duffing吸引子h=2e-3;x0=0:h:180;[y1,~]=ODE_RK4_hyh(x0,h,[1;0.5],{'Duffing',[1.15,1,1]});Lx=y1(1,:);Ly=y1(2,:);figure(6)subplot(1,3,1)plot(Lx,Ly);title('d=1.15')
[y1,~]=ODE_RK4_hyh(x0,h,[0.8;0.75],{'Duffing',[1.35,1,1]});Lx=y1(1,:);Ly=y1(2,:);figure(6)subplot(1,3,2)plot(Lx,Ly);title('d=1.35')
[y1,~]=ODE_RK4_hyh(x0,h,[0.7;0.73],{'Duffing',[1.5,1,1]});%[0.7;0.73]Lx=y1(1,:);Ly=y1(2,:);figure(6)subplot(1,3,3)plot(Lx,Ly);title('d=1.5')
function [F,Output]=Fdydx(x,y,Input)%形式为Y'=F(x,Y)的方程，参见数值分析求解常系数微分方程相关知识%高次用列向量表示，F=[dy(1);dy(2)];y(1)为函数，y(2)为函数导数switch Input{1}    case 'Lorenz'        a=Input{2}(1);b=Input{2}(2);r=Input{2}(3);        dy(1)=a*(y(2)-y(1));        dy(2)=r*y(1)-y(2)-y(1)*y(3);        dy(3)=y(1)*y(2)-b*y(3);        F=[dy(1);dy(2);dy(3)];    case 'Rossler'        a=Input{2}(1);b=Input{2}(2);c=Input{2}(3);        dy(1)=-y(2)-y(3);        dy(2)=y(1)+a*y(2);        dy(3)=b+y(3)*(y(1)-c);        F=[dy(1);dy(2);dy(3)];    case 'Duffing'        d=Input{2}(1);r=Input{2}(2);w=Input{2}(3);        dy(1)=y(2);        dy(2)=-y(1)^3+y(1)-d*y(2)+r*cos(w*x);        F=[dy(1);dy(2)];endOutput=[];end
function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)%4阶RK方法%h间隔为常数的算法y=zeros(size(y0,1),size(x,2));y(:,1)=y0;for ii=1:length(x)-1    yn=y(:,ii);    xn=x(ii);    [K1,~]=Fdydx(xn    ,yn       ,Input);    [K2,~]=Fdydx(xn+h/2,yn+h/2*K1,Input);    [K3,~]=Fdydx(xn+h/2,yn+h/2*K2,Input);    [K4,~]=Fdydx(xn+h  ,yn+h*K3  ,Input);    y(:,ii+1)=yn+h/6*(K1+2*K2+2*K3+K4);endOutput=[];end