BZOJ 2143 飞飞侠（线段树优化建边 / 并查集优化最短路）BZOJ修复工程

Posted 2021-10-29 繁凡さん

整理的算法模板合集： ACM模板

点我看算法全家桶系列！！！

实际上是一个全新的精炼模板整合计划

---

题目链接

https://hydro.ac/d/bzoj/p/2143

是 hydro 的 BZOJ 修复工程 ！（我也去领了一点题慢慢修着玩，这题就是我修的嘿嘿嘿）

题目描述

飞飞国是一个传说中的国度，国家的居民叫做飞飞侠。飞飞国是一个 $N\times M$ 的矩形方阵，每个格子代表一个街区。然而飞飞国是没有交通工具的。飞飞侠完全靠地面的弹射装置来移动。每个街区都装有弹射装置。使用弹射装置是需要支付一定费用的。而且每个弹射装置都有自己的弹射能力。我们设第 $i$ 行第 $j$ 列的弹射装置有 $A_{ij}$ 的费用和 $B_{ij}$ 的弹射能力。并规定有相邻边的格子间距离是 $1$ 。那么，任何飞飞侠都只需要在 $(i,j)$ 支付 $A_{ij}$ 的费用就可以任意选择弹到距离不超过 $B_{ij}$ 的位置了。如下图

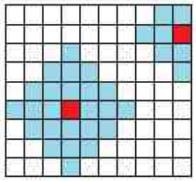
（从红色街区交费以后可以跳到周围的任意蓝色街区。）

现在的问题很简单。有三个飞飞侠，分别叫做 $X$，$Y$，$Z$。现在它们决定聚在一起玩，于是想往其中一人的位置集合。告诉你 $3$ 个飞飞侠的坐标，求往哪里集合大家需要花的费用总和最低。

输入格式

输入的第一行包含两个整数 $N$ 和 $M$ ，分别表示行数和列数。接下来是 $2$ 个 $N\times M$ 的自然数矩阵，为 $A_{ij}$ 和 $B_{ij}$ 最后一行六个数，分别代表 $X$，$Y$，$Z$ 所在地的行号和列号。

输出格式

第一行输出一个字符 $X$、$Y$ 或者 $Z$，表示最优集合地点。

第二行输出一个整数，表示最小费用。

如果无法集合，只输出一行 NO

输入样例

4 4
0 0 0 0
1 2 2 0
0 2 2 1
0 0 0 0
5 5 5 5
5 5 5 5
5 5 5 5
5 5 5 5
2 1 3 4 2 2

输出样例

Z
15

数据规模与约定

对于 $100\%$ 的数据， $1\le N,M\le 150$，$0\le A_{ij}\le 10^9$，$0\le B_{ij}\le 1000$。

Solution

本题看起来就是一道最短路模板题，我们只需要连边之后，跑三次 Dijkstra，然后 DP 计算最小总距离即可。

但是本题 $n\le 150$，给定的是一个 $N\times M$ 的矩阵，假设 $m=n$，也就是一共有 $n^2$ 级别的点的数量，每个点连边的方式比较特殊，它会与四周距离小于 $B_{ij}$ 的点均有费用为 $A_{ij}$ 的边，每个点会连 $n^2$ 规模的边，直接暴力连边时间复杂度为 $O(n^4)$ ，时间勉强卡过，空间无法承受。

考虑优化。

优化一

发现本题的模型是一个点向一个区间连边。显然可以使用线段树优化建边，我们直接对每一行建一个线段树，行内优化连边 $O(n)\to O(\log n)$，连边时间复杂度和空间复杂度为 $O(n^3\log n)$，跑 Dijkstra 时间复杂度 $O(n^3\log n\log (n^3\log n))$，可以通过本题。

Code

代码详见：https://www.luogu.com.cn/blog/wucstdio/solution-p4473

优化二

考虑本题时间上可以勉强承受，空间上承受不能，所以我们考虑能否优化空间。对于每一个点，我们发现它能到达的点是可以直接枚举计算出来的，所以我们可以不进行建图，在 Dijkstra 转移的时候直接枚举能到达的点，这样就免去了建图，空间足够了，暴力转移，时间复杂度 $O(n^4)$，可以勉强通过本题。

Code

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int maxn = 150 + 7, INF = 0x3f3f3f3f;

int n, m, s, t, ans;
int A[maxn][maxn], B[maxn][maxn];
int X[maxn], Y[maxn];
ll path[maxn][maxn];
ll dist[maxn][maxn];

struct node
{
	int x, y;
	ll d;
	bool operator < (const node &t) const {
		return d > t.d;
	}
};

void Dijkstra(int s)
{
	priority_queue<node> q;
	memset(dist, 0x3f, sizeof dist);
	dist[X[s]][Y[s]] = 0;
	q.push((node){X[s], Y[s], 0ll});
	while(q.size()) {
		node u = q.top();
		q.pop();
		if(dist[u.x][u.y] != u.d) continue;
		int len = B[u.x][u.y];
		int cost = A[u.x][u.y];
		for (int i = max(1, u.x - len); i <= min(n, u.x + len); ++ i) {
			int updown = len - abs(u.x - i);
			for (int j = max(1, u.y - updown); j <= min(m, u.y + updown); ++ j) {
				if(dist[i][j] > dist[u.x][u.y] + cost) {
					dist[i][j] = dist[u.x][u.y] + cost;
					q.push((node){i, j, dist[i][j]});
				}
			}
		}
	}
	for (int i = 1; i <= 3; ++ i)
		path[s][i] = dist[X[i]][Y[i]];
}
char name[10] = "1XYZ";

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; ++ i) 
		for (int j = 1; j <= m; ++ j)
			scanf("%d", &B[i][j]);
	
	for (int i = 1; i <= n; ++ i) 
		for (int j = 1; j <= m; ++ j)
			scanf("%d", &A[i][j]);
	for (int i = 1; i <= 3; ++ i)
		scanf("%d%d", &X[i], &Y[i]);
		
	for (int i = 1; i <= 3; ++ i)
		Dijkstra(i);
	ll ans = INF;
	int id = -1;
	for (int i = 1; i <= 3; ++ i) {
		ll sum = 0;
		for (int j = 1; j <= 3; ++ j)
			sum += path[j][i];
		if(ans > sum)
			ans = sum, id = i;
	}
	if(ans == INF)
		return 0 * puts("NO");
	cout << name[id] <<endl;
	cout << ans << endl;
	return 0;
}

最慢一个点 840ms/6.14MB

优化三

优化二的思路太过暴力，考虑能否优化时间复杂度。

我们从本题图的特殊性质出发分析。

发现本题是一个特殊的图，每个点能走到的点在一个范围区间之内，显然从一个起点出发跑最短路，走到一个点之后，再往下走，如果最后又回到这个点，回头了以后，显然此时到这个点的路径长度一定比之前到达这个点时更新的最短路更大，也就是说这种图有一个特殊的性质，即一个点没必要走两次，第二次走到的时候也不可能更优，就没必要再回头了，所以如果我们可以让我们走的时候不会回头，就会达到一个非常优秀的优化效果，我们把已经更新的点放进一个并查集内，根节点指向最右边节点的 下一个点 。这样当我们第二次进入这个节点时，可以 $O(1)$ 地跳过当前所有节点。路径压缩之后，下次如果又回到了这个点，我们就可以直接 $O(1)$ 跳过所有已经走过的点。

在插入堆的时候，我们需要比较 $dist[i]+w[i]$ 而不是 $dis[i]$ ，这样可以保证一个点被更新后不会再一次被更新。

并查集优化之后时间复杂度来到了神奇的 $O(n^2\log bzoj2143:\; 飞飞侠$

刷题总结——飞飞侠(bzoj2143 最短路)

bzoj2143 飞飞侠

bzoj 2143:飞飞侠

bzoj 2143: 飞飞侠

BZOJ2143 飞飞侠 最短路