数据结构与算法碎片积累

Posted 2021-10-28 鸿_H

前言：这系列时间间隔了半年，是时候更完这余下近30节课程笔记啦。不然，得在硬盘里面发霉了。

1.查找算法

1）按照查找方式来分，可分为，静态查找和动态查找

静态查找，要求数据集合稳定，不需要添加、删除元素的一种查找操作

动态查找，要求数据集合，在查找过程中，需要同时添加或删除元素的一种查找操作

2）对于动态查找来说，可以使用线性表结构组织数据，这样可以使用顺序查找算法，如果再对关键字进行排序，则可以使用折半查找算法或裴波拉契查找算法等来提高查找的效率

3）对于动态查找来说，则可以考虑二叉树排序树的查找技术，另外还可以使用散列表结构来解决一些查找问题。

4）顺序查找又叫线性查找，是最基本的查找技术。其查找过程是，从第一个（或者最后一个）记录开始，逐个记录的关键字和给定值进行比较，若某个记录的关键字和给定值相等，则查找成功。如果查找了所有记录仍然找不到与给定的值相等，则查找不成功。对于查找结果，都应该给出相应的提示操作

//顺序查找，a为查找的数组，n为要查找的数组的长度，key为要查找的关键字
int Sq_Search(int* a, int n, int key) {
	int i;
	for (i = 1; i <= n; i++) {
		if (a[i] == key) {
			return i;
		}
	}
	return 0;
}//判断加循环，2n次

int Sq_Search_(int* a, int n, int key) {
	int i = n;
	a[0] = key;
	while (a[i]!=key)//从下标最大值开始往回找
	{
		i--;
	}

	return i;//放回0就表示没有找到
}//判断加循环，n次，效率较上一个提升一倍

2、插值查找（按比例查找）

折半查找的基本思想：减少查找序列的长度，分而治之地进行关键字的查找

折半查找的实现过程：先确定待查找记录的所在范围，然后逐渐缩小这个范围，直到找到该记录或查找失败（查无记录）为止（low,mid,high）

这里的插值查找，关键是修改mid的位置，折半的话，其都是一半的，而插值mid就是可改变的了。

#include<stdio.h>

//插值查找算法
int bin_search(int str[], int n, int key) {
	int low, high, mid;

	low = 0;
	high = n-1;
	
	//注意，这些数据都是按照从小到达排序好的
	while (low<=high)
	{
		mid = low + (key - str[low] )/( str[high] - str[low]) * (high - low);	//插值查找的唯一不同点,相对折半查找算法而言

		if (str[mid] == key) {
			return mid;
		}
		if (str[mid] < key) {
			low = mid + 1;
		}
		if (str[mid] > key) {
			high = mid - 1;
		}
	}
	return -1;
}
//时间复杂度为O（log2n）

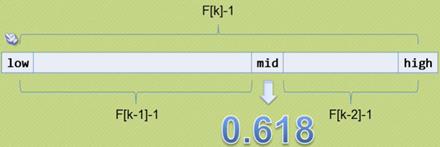
3、裴波拉契查找（黄金分割算法查找）

裴波拉契数列（F[k]）【从第三项开始，本身就是前两项之和】
1,1,2,3,5,8,13,21,34,55,89,…

4、线性索引查找

1）稠密索引

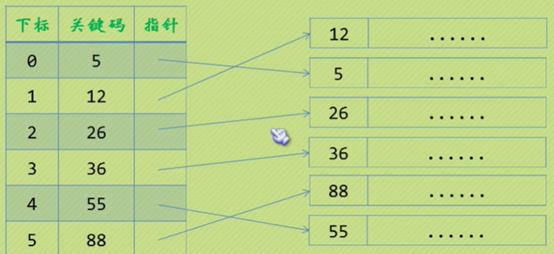
稠密索引，应用在数据量不是特别大情况下。

2）分块索引

分块索引，块内无序。

3）倒排索引

这个属于搜索引擎的原理；倒排索引应用在数据量很大情况。

这三个索引，只做一个感性认识，具体的话还是得好好找点资料来看。

5、二叉树排序树

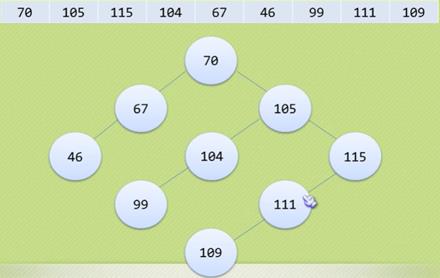
将上面的列表数据转换为二叉排序树；以第一个70作为根节点，大于则右边，小于则左边，进入下一个节点也是如此比对。可以使用二叉树生成的知识，编程实现二叉排序树。

二叉排序树（binary sort tree）又称为二叉查找树，其或者是一棵空树，或者是具有下列性质的二叉树：
----若其左子树不为空，则左子树上所有结点的值均小于其根结构的值
----若其右子树不为空，则右子树上所有结点的值均大于其根结构的值；
----其左、右子树也分别为二叉排序树（递归）

6、二叉树的查找、插入和删除

删除参考图

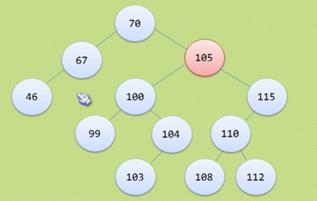
//200203
#include<stdio.h>
#include <malloc.h>


#define Status int
#define FALSE 0
#define TRUE 1

//二叉树的二叉链表结点结构定义
typedef struct BiTNode {
	int data;
	struct BiTNode* lchild, * rchild;
}BiTNode,*BiTree;

//递归查找二叉树T中是否存在key
//指针f指向T的双亲，其初始值调用值为NULL
//若查找成功，则指针p指向该数据元素结点，并返回TRUE
//否则指针p指向查找路径上访问的最后一个结点，并返回FALSE

//查找
Status SearchBST(BiTree T, int key, BiTree f, BiTree* p) {
	if (!T) {//查找不成功
		*p = f;
		return FALSE;
	}
	else if (key==T->data)		//查找成功
	{
		*p = T;
		return TRUE;
	}
	else if (key < T->data) {
		return SearchBST(T->lchild, key,T, p);	//在左子树继续查找
	}
	else
	{
		return SearchBST(T->rchild, key, T, p);	//在右子树继续查找
	}

}

//插入
Status InsertBST(BiTree* T, int key) {
	BiTree p, s;
	if (!SearchBST(*T, key, NULL, &p)) {//树中没有关键字相同节点，可插入

		//初始化待插入节点
		s = (BiTree)malloc(sizeof(BiTNode));
		s->data = key;
		s->lchild = s->rchild = NULL;

		if (!p) {	//查找不到key。（并且是一颗空树情况。201010）
			*T = s;	//插入s为新的根结点
		}
		else if (key < p->data) {
			p->lchild = s;	//插入s为左孩子
		}
		else
		{
			p->rchild = s;	//插入s为右孩子
		}
		return TRUE;
	}
	else
	{
		return FALSE;	//树中已有关键字相同的结点，不再插入
	}
}
//上面的查找和插入，可以用于创建二叉树


//删除
//情况1，待删除的是叶子结点，直接删除即可
//情况2，待删除的结点，仅有左子树或者右子树，删除后直接连接其的上一结点（自己的根结点）即可
//情况3，待删除的结点，既有左子树，又有右子树，可以其左子树的最大的或者其右子树最小的替换自身位置
Status DeleteBST(BiTree* T, int key) {
	if (!*T) {		//没有找到（空树并不需要进行删除操作211010）
		return FALSE;
	}
	else
	{
		if (key == (*T)->data) {
			return Delete(T);
		}
		else if (key > (*T)->data) {
			return DeleteBST(&(*T)->lchild, key);
		}
		else
		{
			return DeleteBST(&(*T)->rchild, key);
		}
	}
}

Status Delete(BiTree* p) {
	BiTree q, s;

	if ((*p)->rchild == NULL) {		//右子树为空情况下
		q = *p;
		*p = (*p)->lchild;
		free(q);
	}
	else if ((*p)->lchild == NULL) {	//左子树为空情况下
		q = *p;
		*p = (*p)->rchild;
		free(q);
	}
	else                             //左子树、右子树均不为空情况下
	{						//这里展示的是，删除点的左子树最大替换的方式		
		q = *p;
		s = (*p)->lchild;

		while (s->rchild)	//待删除结点存在右子树，目的找到左子树中的最大值
							//这里感觉这二叉树是排好序的，并且右节点比左节点大，满足lchild<rchild关系,注意不保证lchild<mid<rchild的（211010）
		{
			q = s;
			s = s->rchild;
		}

		(*p)->data = s->data;	//将上述的右子树中的最大值替换到删除点位置

		if (q != *p) {		//当其结点不与待删除结点相等时
			q->rchild = s->lchild;	//将最大值对应的结点s的左子树连接到其上一结点的右子树处
		}
		else            //当其结点与待删除结点相等时
		{
			q->lchild = s->lchild;//将最大值对应的结点s的左子树连接到其上一结点的左子树处
		}

		free(s);
	}
	return TRUE;
}
//理解得一半一半。。。简单理解，理解失败。

#########################
不积硅步，无以至千里
好记性不如烂笔头
感谢小甲鱼老师
截图权利归原作者所有