一文通数据结构与算法之——贪心算法+常见题型与解题策略+Leetcode经典题

Posted 尚墨1111

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了一文通数据结构与算法之——贪心算法+常见题型与解题策略+Leetcode经典题相关的知识，希望对你有一定的参考价值。

文章目录

贪心算法

1 概念

1.1 心得

  • 贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

  • 往往最平淡无奇、看似毫无技巧的方法，可能就是贪心。返璞归真。

    • 比如：加油站问题只是求个总和，找和最小的地方

  • 我们要找到组成题目元素中最有价值的点是什么，从而求局部最优解，再拓展到全局最优

    • 比如分饼干，大的饼干喂胃口最大的孩子，实现饼干价值最大化
    • 比如柠檬水找零，5块既可以找10块的零，也可以找20的零是最有价值的，所以我们尽可能保留最多的

1.2 题目列表

2 Leetcode经典题

2.1 分发物品

135.分发糖果(非常经典)

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。问最少的糖果

  • 每个孩子至少分配到 1 个糖果。
  • 评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果。

局部最优：左右分别遍历一遍，每个元素取left和right的最大值就是局部最优，n个元素都是最优就是全局最优了

	public int candy(int[] ratings) {
        int n = ratings.length;
        int[] left = new int[n];
        int[] right = new int[n];
        for (int i = 1; i < n; i++) {
            if(ratings[i]>ratings[i-1]){
                left[i] = left[i-1]+1;
            }
        }
        int count = left[n-1]+n;
        for (int i = n-2; i >=0 ; i--) {
            if(ratings[i]>ratings[i+1]){
                right[i] = right[i+1]+1;
            }
            count+=Math.max(right[i],left[i]);
        }
        return count;
    }

455.分发饼干

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

输入: g = [1,2,3], s = [1,1]
输出: 1

**局部最优：**大饼干喂给胃口大的，让大饼干的价值最大化，**全局最优：**喂饱尽可能多的小孩。

	public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(s);
        Arrays.sort(g);
        int count=0;
        int i = s.length-1,j = g.length-1;
        while(i>=0 && j>=0){
            if(s[i]>=g[j]){
                count++;
                i--;
                j--;
            }else{
                j--;
            }
        }
        return count;
    }

860. 柠檬水找零

每一杯柠檬水的售价为 5 美元。每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。一开始你手头没有任何零钱。给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false

输入：bills = [5,5,5,10,20]
输出：true

思路：局部最优：5元可以找零10、20，尽可能的保留5元，就能尽可能的找零更多的顾客。全局最优：全部顾客都成功找零

	public boolean lemonadeChange(int[] bills) {
        int count5 = 0;
        int count10 = 0;
//        1.遍历数组，记录5元10元个数
        for (int i = 0; i < bills.length; i++) {
            if(bills[i]==5){
                count5++;
            }else if(bills[i]==10){
                if(count5==0){
                    return false;
                }else{
                    count5--;
                    count10++;
                }
            }else{
                //2.局部最优，先用10块的，保留5块的
                if(count10>0 && count5>0){
                    count10--;
                    count5--;
                }else if(count5>3){
                    count5-=3;
                }else{
                    return false;
                }
            }
        }
        return true;
    }

2.2 数组序列相关

1005. K 次取反后最大化的数组和

给定一个整数数组 A，我们只能用以下方法修改该数组：我们选择某个索引 i 并将 A[i] 替换为 -A[i]，然后总共重复这个过程 K 次。我们可以多次选择同一个索引 i。以这种方式修改数组后，返回数组可能的最大和。

输入：A = [3,-1,0,2], K = 3
输出：6

思路：**局部最优：**每次选取最小的元素变，影响最小，全局最优：总和自然也是最大的。

public int largestSumAfterKNegations(int[] nums, int k) {
        if(nums==null || nums.length==0){
            return 0;
        }
        Arrays.sort(nums);
        int index = 0;
        while(k>0){
//        1.每次把最小的反转，总和也是最大的
            nums[index] = -nums[index];
            k--;
//        2.重新确定最小元素
//        每次取反之后只会影响自身，只需要比较前后两个元素的大小关系，就是最小的元素
//        我原来的思路是重新排一次序，但是效率太低了。
            if(index+1< nums.length && nums[index]>nums[index+1]){
                index++;
            }
        }
        int sum = 0;
        for (int num : nums) {
            sum +=num;
        }
        return sum;
    }

376. 摆动序列

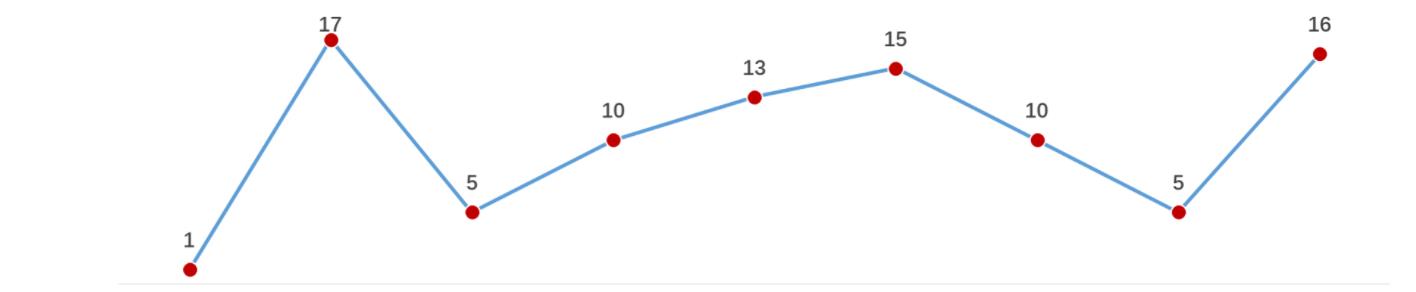
如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 **摆动序列 。**给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

输入：nums = [1,7,4,9,2,5]
输出：6

思路：局部最优：局部的峰值个数之和，全局最优：就是全局最长的摆动子序列

记录两边的差值

	public int wiggleMaxLength(int[] nums) {
//        1.记录两边的差值,因为两端的默认是摆动部分，所以pre=0
        int pre = 0;
        int after = 0;
        int count = 1;
//        2.遍历每一个元素，找波峰、波谷
        for (int i = 1; i < nums.length; i++) {
            after = nums[i]-nums[i-1];
            if(pre<=0 && after>0 ||pre>=0 && after<0){
                count++;
                pre = after;
            }
        }
        return count;
    }

738. 单调递增的数字

给定一个非负整数 N，找出小于或等于 N 的最大的整数，同时这个整数需要满足其各个位数上的数字是单调递增。

输入: N = 332
输出: 299

局部最优：从左往右遍历各位数字，找到第一个开始下降的数字[i]，将[i]减1，然后将[i+1 …]各位数字全部置为9即可

注意：有相等的情况，33332，要找到第一个3——29999

事实证明：直接修改char数组的效率要比 StringBuilder的效率要高

	public int monotoneIncreasingDigits(int n) {
//        1.特殊情况排除
        if(n<10){
            return n;
        }
        char[] ch = String.valueOf(n).toCharArray();
        int start = 0;
//         2.找到第一个下降的数字， 232—— 3
        while(start<ch.length-1 && ch[start]<=ch[start+1]){
            start++;
        }
//        3.判断这个是否为末尾
        if(start==ch.length-1){
            return n;
        }
//        4.判断前面是否有相同的元素
        while(start>0 && ch[start]==ch[start-1]){
            start--;
        }
//        5.变元素,直接修改char数组的效率要比 StringBuilder的效率要高
        ch[start++] = (char)(ch[start]-1);
        while(start<ch.length){
            ch[start++] = '9';
        }
        return Integer.parseInt(String.valueOf(ch));
    }

122. 买卖股票的最佳时机 II

给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。你可以多次买卖一支股票，你必须在再次购买前出售掉之前的股票，求最大利润

输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

思路：如果可以把所有的上坡全部收集到，一定是利益最大化的，相比于我刻意计算波峰波谷，这不就直接前后比较大小就可

	public int maxProfit(int[] prices) {
        int res = 0;
        for (int i = 1; i < prices.length; i++) {
            if(prices[i]-prices[i-1]>0){
                res+=(prices[i]-prices[i-1]);
            }
        }
        return res;
    }

55. 跳跃游戏

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标。

输入：nums = [2,3,1,1,4]——[2,4,4,5,8]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

局部最优：如果一个位置能够到达，那么这个位置左侧所有位置都能到达。

	public boolean canJump(int[] nums) {
//      1.特殊情况的排除
        if(nums==null){
            return false;
        }
//      2.遍历所有元素，维护最长可达到距离
        int max = 0;
        for (int i = 0; i < nums.length; i++) {
            max = Math.max(max,nums[i]+i);
//      3.如果当前位置到达的位置小于索引，且不是终点代表不能到达，比如[2,0]既可以到达
            if(max<=i && max<nums.length-1){
                return false;
            }
        }
        return true;
    }

45. 跳跃游戏 II

给你一个非负整数数组 nums ，你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。你的目标是使用最少的跳跃次数到达数组的最后一个位置。假设你总是可以到达数组的最后一个位置。

输入: nums = [2,3,1,1,4]
输出: 2

局部最优：维护每一步能到的最大距离，超过最大距离，记为下一步，一旦这个距离大于数组长度，就里面返回

	public int jump(int[] nums) {
        //1.排除特殊情况
        if(nums==null || nums.length<=1){
            return 0;
        }
        int max = 0,end = 0,count=0;
//        2.注意边界，因为最后一步肯定会跳到端点，所以num.length-1，不然在边界刚刚好是num.length时会多算一次
        for (int i = 0; i < nums.length-1; i++) {
            max = Math.max(nums[i]+i,max);
//		  3.如果从这个跳点 起跳叫做第 1 次 跳跃,最长可以跳3步，那么在后面 3 个格子起跳 都叫做第 2 次 跳跃。
//            所以只有当i达到第二次能跳到的最大距离，才计步数
            if(i==end){
                end = max;
                count++;
            }
        }
        return count;
    }

2.3 区间类题目：

406. 根据身高重建队列

套路：一般这种数对，还涉及排序的，根据第一个元素正向排序，根据第二个元素反向排序，或者根据第一个元素反向排序，根据第二个元素正向排序，往往能够简化解题过程。

假设有打乱顺序的一群人站成一个队列，数组 people 表示,每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面 正好 有 ki 个身高大于或等于 hi 的人。请你重新构造并返回输入数组 people 所表示的队列。

输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]

根据题目要求应该为身高降序，也就是说先考虑把身高较高的人放入新集合，这样在高个子前面或后面插入矮个子都不会影响当前高个子的k值；其次，k值应该升序排列，k值较大的较后插入。

	public int[][] reconstructQueue(int[][] people) {
//        首先先将数组按第一个元素身高降序，按第二个元素人数升序
        Arrays.sort(people,(p1,p2)->p1[0]==p2[0]?p1[1]-p2[1]:p2[0]-p1[0]);
        List<int[]> list = new ArrayList<>();
        for (int i = 0; i < people.length; i++) {
//            1.如果k值大于现在的长度，说明他的位置还在后面，直接插入
            if(people[i][1]>=list.size()){
                list.add(people[i]);
            }else{
                //2.否则把它插入对应的位
以上是关于一文通数据结构与算法之——贪心算法+常见题型与解题策略+Leetcode经典题的主要内容，如果未能解决你的问题，请参考以下文章
 

 一文通数据结构与算法之——数组+常见题型与解题策略+Leetcode经典题


 一文通数据结构与算法之——链表+常见题型与解题策略+Leetcode经典题


 一文通数据结构与算法之——二叉树+常见题型与解题策略+Leetcode经典题


 一文通数据结构与算法之——图+常见题型与解题策略+Leetcode经典题


 一网打尽！二分查找解题模版与题型全面解析


 Python数据结构与算法篇-- 链表的应用与常见题型