大数定律中心极限定理点估计区间估计

Posted 2021-10-28 hellobigorange

首先，以统计全国平均身高引入大数定律和中心极限定理：

我们要调查全国人口(假设有P人($X_1,X_2,...,X_P$)，且服从均匀分布，均值$\mu$，方差${\delta }^2$)的平均身高：

• 大数定律
  现在抽样调查了n个人，大数定律的思想告诉我们：当样本量n足够大时，样本均值可以近似总体均值（（$\frac{{\Sigma }_{i=1}^n{X}_i}{n}=\mu ,n\to \infty$），这样我们会得到全国人口的平均身高。

• 中心极限定理
  中心极限的思想重复抽样N次，每次取样n人并计算样本均值，当n足够大时，样本均值(看作一个新的随机变量)（$\frac{{\Sigma }_{i=1}^n{X}_i}{n}$）服从正态分布($N(\mu ,{\delta }^2/n)$)。

• 点估计
  给出平均身高的估计值，但不能给出估计值偏离真实值的程度。

• 区间估计：95%的置信水平认为全国人口身高落在[164，165.5]

  • 置信区间：随机抽样n个人，计算样本均值和标准误差（标准差/$\sqrt{(}n)$），确定需要的置信水平，根据这三者可以确定该置信水平下的置信空间。
  • 置信水平：落在置信区间的可信度
    直观理解我们最常用的95%置信水平，就是说做100次抽样，每次抽样n个人，计算置信区间，有95次的置信区间包含了总体均值。

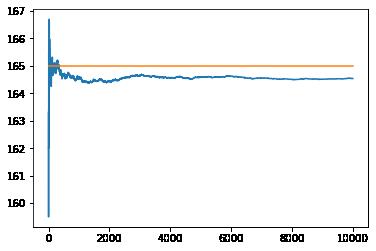
# 验证大数定律
import numpy as np
import matplotlib.pyplot as plt

#假设总体身高服从均匀分布，N=10000，均值（150+180）/2
data = np.random.randint(150,180,10000) 
means = []
for i in range(1,10000):
    means.append(np.mean(data[:i]))
plt.plot(means)
plt.plot([0,10000],[165,165])
plt.show()

# 验证中心极限
import numpy as np
import matplotlib.pyplot as plt

#假设总体身高服从均匀分布，N=10000，均值（150+180）/2
data = np.random.randint(150,180,10000) 
#进行6000次取样
means = []
for i in range(6000):
    tmp = np.random.choice(data,size = 1000)
    means.append(tmp.mean())
#绘制均值们的直方图
plt.grid()
plt.hist(means,30)
plt.show()

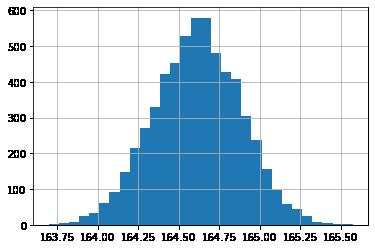
结合上面两个图，重复实验6000次，大概有95%的样本均值都会落在[164，165.5]的区间内。其实，区间估计就是根据中心极限定理得到的。