CS224W摘要14.Traditional Generative Models for Graphs

Posted 2021-10-28 oldmao_2000

文章目录

• Properties of Real-world Graphs
• • Degree distribution
  • Clustering coefficient
  • Connectivity
  • Path Length
• MSN Graph
• Erdös-Renyi Random Graphs
• • Degree distribution of $G_{np}$
  • Clustering Coefficient of $G_{np}$
  • $G_{np}$的连通分量
  • Expansion
  • Shortest Path of $G_{np}$
  • MSN vs $G_{np}$
• The Small-World Model
• • 创建步骤
  • 结果及分析
  • 小结
• Kronecker Graph Model
• • 生成步骤
  • 快速版生成步骤
• 总结

CS224W: Machine Learning with Graphs
公式输入请参考： 在线Latex公式
这节和下节都是讲图的生成模型，这节讲传统方法，下节讲DL方法。
之前学习的内容都是给定图，然后学习这个图的特征，做特定的预测节点、边等任务：

这节开始研究如何用模型生成这样的图。

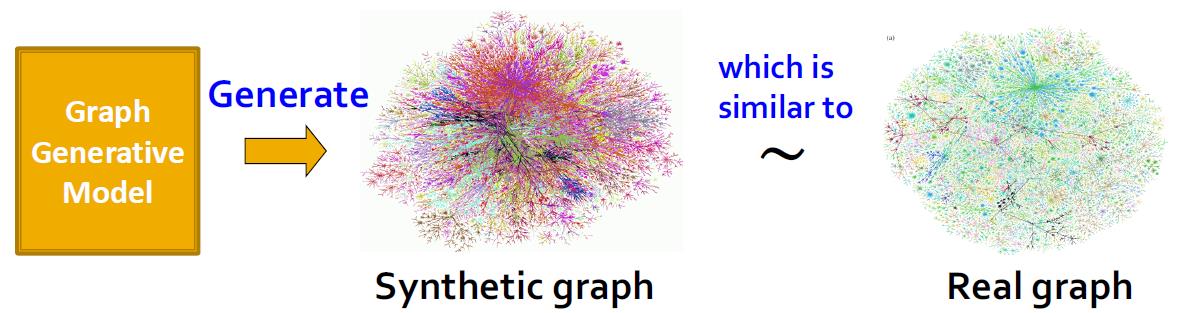
几个好处：
Insights – We can understand the formulation of graphs
Predictions – We can predict how will the graph further evolve
Simulations – We can use the same process to general novel graph instances
Anomaly detection - We can decide if a graph is normal / abnormal

这块图生成模型分三块来讲，第一块先复习真实图的基本属性；第二块学习传统图生成模型；第三块学习深度图生成模型（下节讲）。

Properties of Real-world Graphs

这块基本属于复习，基本前面都有讲过这些内容（Lecture 1&2）。
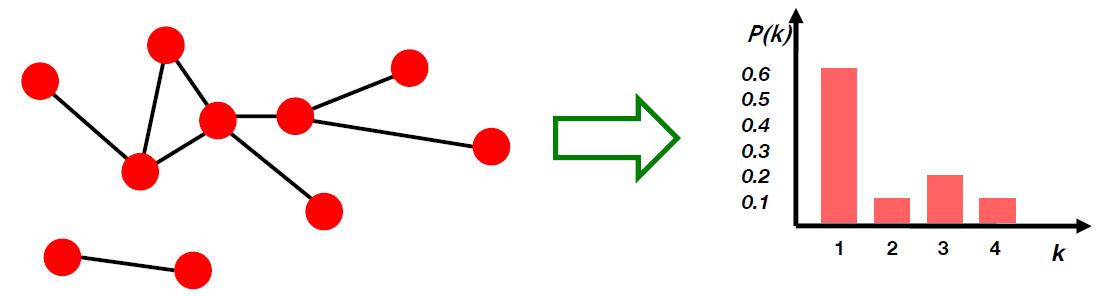
Degree distribution: $P(k)$
Clustering coefficient: $C$
Connected components: $s$
Path length: $h$

Degree distribution

记随机选择的节点拥有度为$k$的概率：$P(k)$
记有$N_k$个节点拥有度为$k$，则：
$$P(k)=\frac{N_k}{N}$$

Clustering coefficient

聚集系数，用来衡量节点$i$的邻居的相互连接程度，记节点$i$的度为$k_i$，则聚集系数为：
$$C_i=\frac{2e_i}{k_i(k_i-1)},C_i\in [0,1]$$

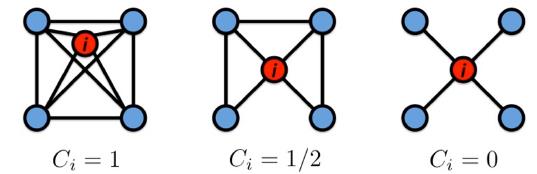
$e_i$是邻居之间的边，不含节点$i$与邻居的边。
整个图的聚集系数是求所有节点的聚集系数后进行平均：
$$C=\frac{1}{N}\sum _i^N{C}_i$$

Connectivity

就是最大连通分量，找出下图的最大连通分量：

步骤：
1.从随机一个节点开始做BFS
2.标记访问过的节点
3.如果所有节点均能访问，则该图是连通图
3.1否则重新找一个未访问的节点从步骤1开始，直到所有图中节点都被访问。

Path Length

图的直径：图中任意节点对的最大的最短路径长度
对于连通无向图或强连通有向图而言，图的平均路径长度为：
$$\bar{h}=\frac{1}{2E_{\max }}\sum _{i,j\ne i}{h}_{ij}$$
其中$h_{ij}$是两个节点之间的距离，$E_{\max }=n(n-1)/2$是图中可包含的最大边数量。
通常在计算过程中，我们会忽略掉路径长度为无穷的值，从而计算出正确的平均路径长度。

有了上面四个属性，下面来看具体实际图的例子。

MSN Graph

MSN Messenger: 只包含 1 month of activity，基本信息如下：
245 million users logged in
180 million users engaged in conversations
More than 30 billion conversations
More than 255 billion exchanged messages

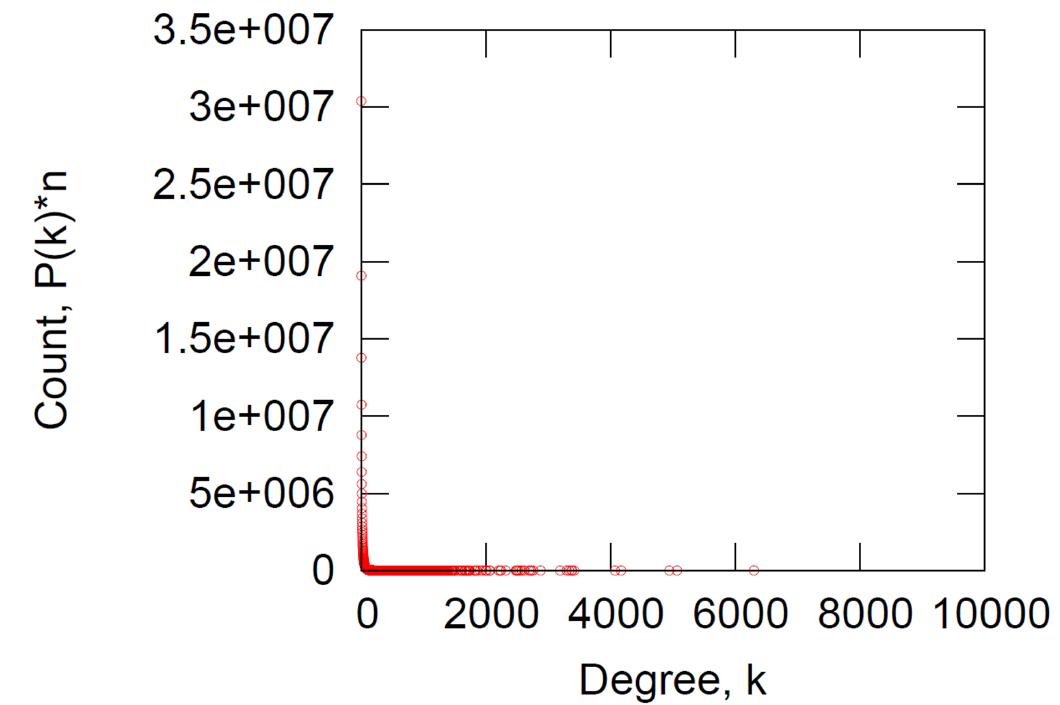
原始度分布，平均度为14.4：

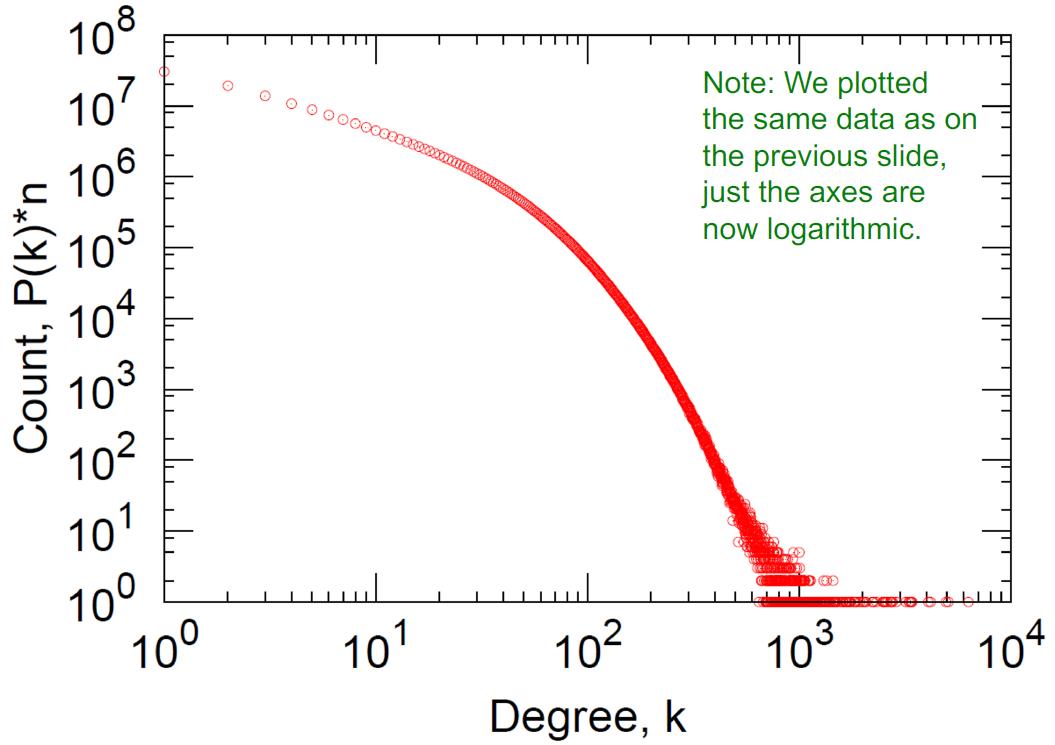
横纵坐标log后的度分布

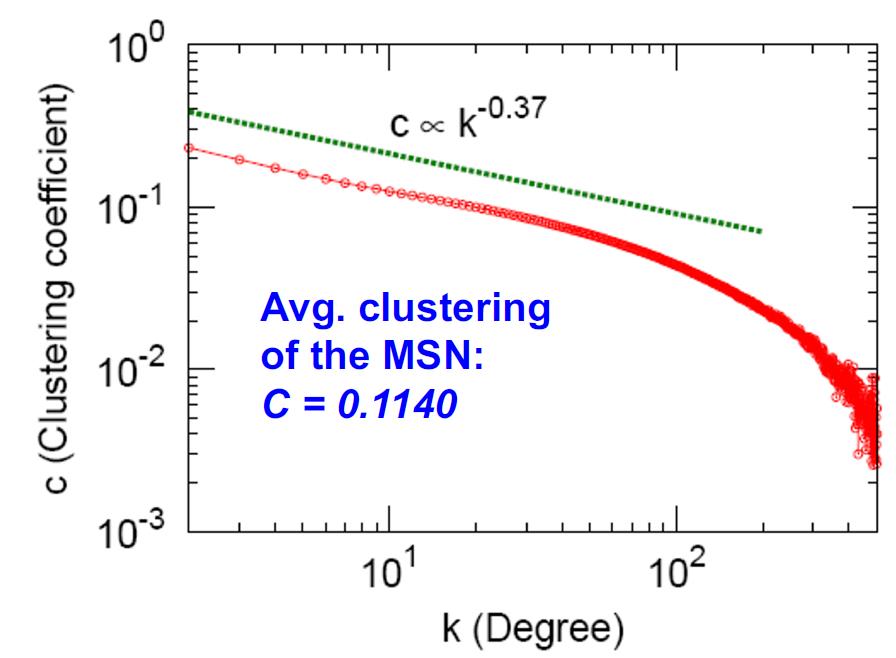
聚集系数：0.114

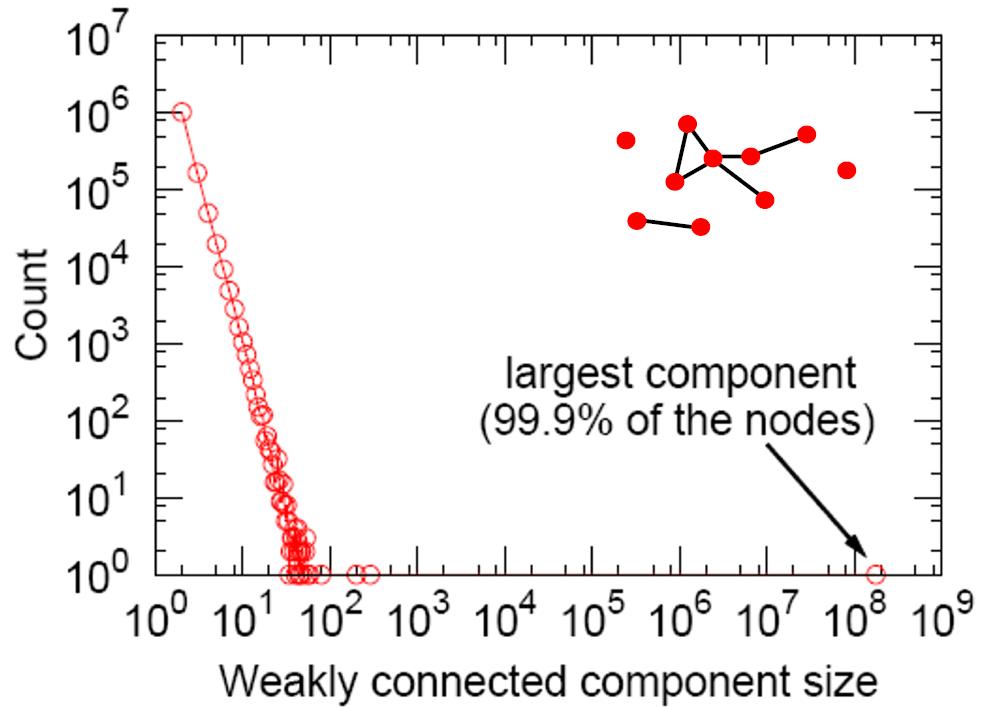
连通分量，最大那个基本涵盖99%的用户。

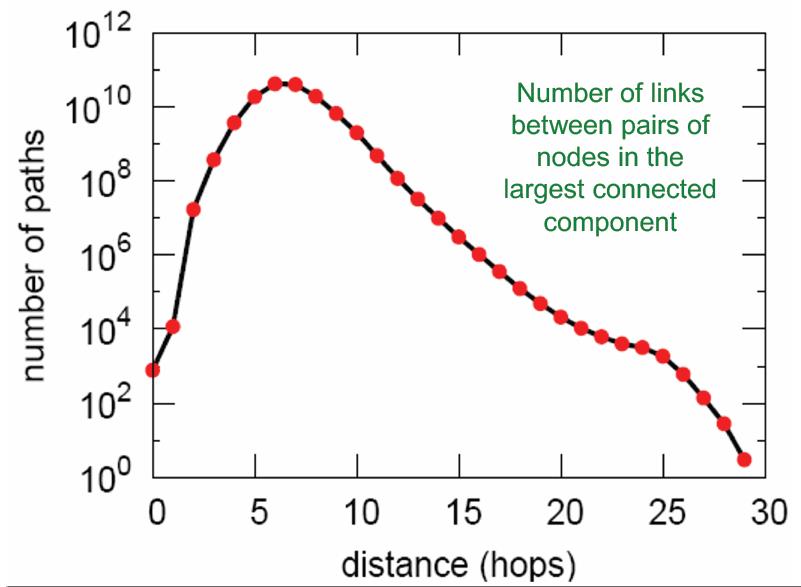
路径长度，平均路径长度为6.6,90%的节点可以在8跳内相互访问。

以上信息没有对比也无法知道这些指标是否偏高或者正常，下面引入三个生成随机图的方法，将生成图与MSN网络进行对比。

Erdös-Renyi Random Graphs

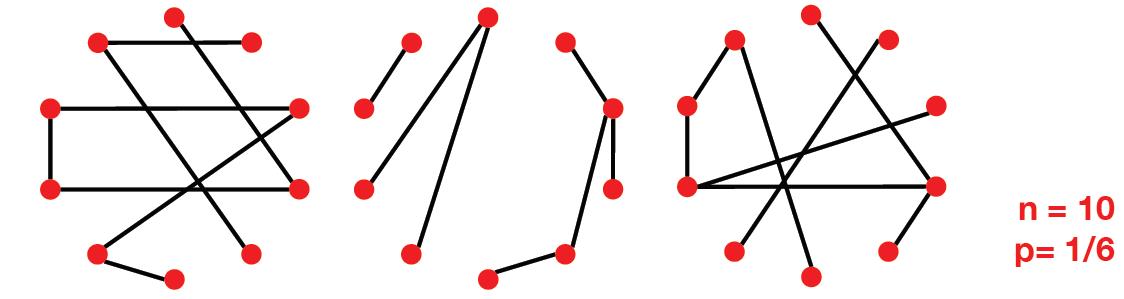
这个方法是两个发明人的名字合体命名的。类似RAS，它有两种形式：
$G_{np}$：表示一个有$n$个节点的无向图，其中每个节点对$(u,v)$是否有边，是按i.i.d.（独立同分布）的概率$p$进行设置的。
$G_{nm}$：表示一个有$n$个节点的无向图，其中随机选择$m$个节点对形成边。
主要看第一种形式。它有两个变量来控制生成图的形式：

下面来看$G_{np}$生成的图的几个属性：

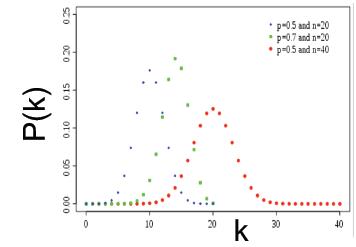
Degree distribution of $G_{np}$

其度分布是一个二项分布：

上面的$n-1$表示是除了当前节点外，从$n-1$个节点中选出$k$个节点，让这$k$个节点与当前节点以概率$p$的方式相连。
该二项分布的均值和方差为：
$$\begin{gathered} \bar{k}=p(n-1) \\ \sigma =p(1-p)(n-1) \end{gathered}$$
看图基本就是高斯分布：

Clustering Coefficient of $G_{np}$

由于图中的边是按i.i.d.（独立同分布）的概率$p$进行设置的。因此，对于节点$i$度为$k_i$而言，其邻居之间出现边的期望可以表示为：
$$E[e_i]=p\frac{k_i(k_i-1)}{2}$$
从而根据原始的聚集系数公式得到期望聚集系数为：
$$CS224W摘要总纲（已完结）$$

CS224W摘要总纲（已完结）

CS224W摘要10.Knowledge Graph Embeddings

CS224W摘要03.Node Embedding

CS224W摘要05.Message passin and Node classification

CS224W摘要15.Deep Generative Models for Graphs