算法入门09矩形覆盖

Posted 2021-10-27 2021dragon

核心考点：场景转化成模型，特殊情况分析，简单dp

我们可以用 $2\times 1$ 的小矩形横着或者竖着去覆盖更大的矩形。请问用n个 $2\times 1$ 的小矩形无重叠地覆盖一个 $2\times n$ 的大矩形，从同一个方向看总共有多少种覆盖的方法？

例如，n=3时，$2\times 3$ 的矩形块有3种覆盖方法（从同一个方向看）：

解析：
对于这道题，我们若是从无到有一个个的放小矩形的话，那么我们迟早会崩溃，因为当我们才放到4个小矩形的时候情况就已经很多了。

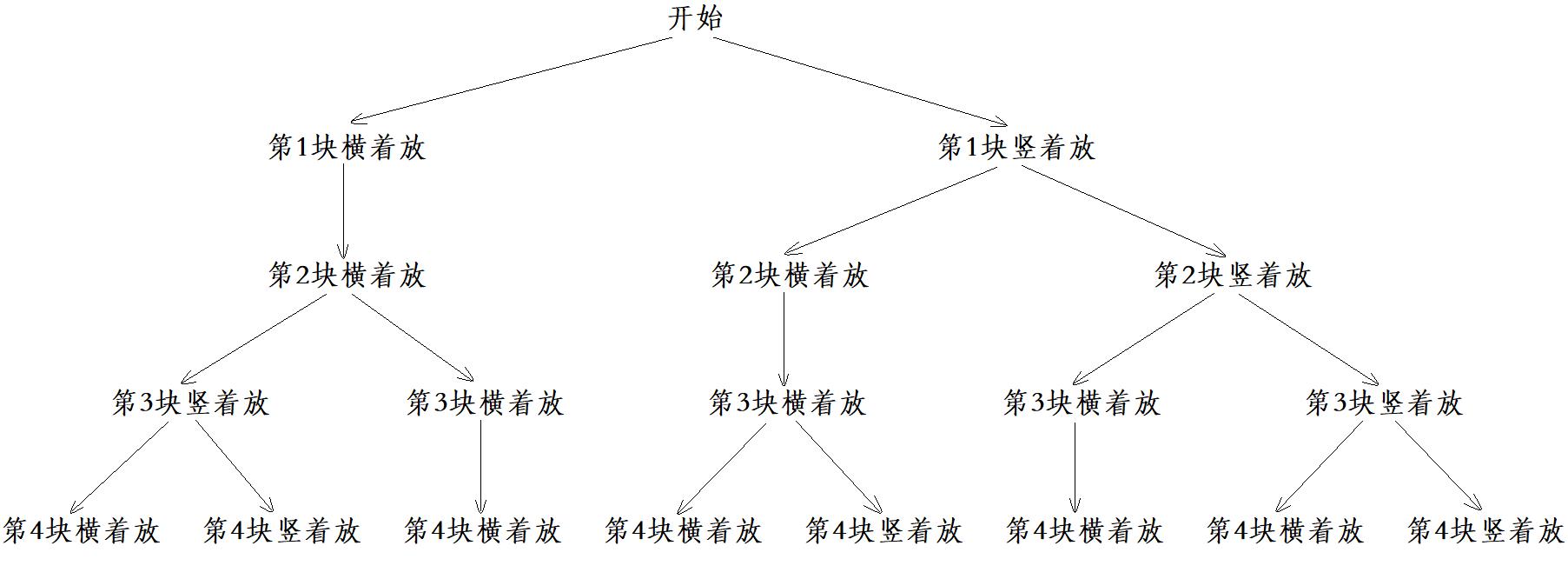
这时我们可以尝试从后往前进行分析，寻找规律。

我们将$f(x)$定义为用 $2\times 1$ 的小矩形无重叠地覆盖一个 $2\times x$ 的大矩形的覆盖总方法数，那么就有如下结论：

表达式	含义
$f(n)$	用 $2\times 1$ 的小矩形无重叠地覆盖一个 $2\times n$ 的大矩形的覆盖总方法数
$f(n-1)$	用 $2\times 1$ 的小矩形无重叠地覆盖一个 $2\times (n-1)$ 的大矩形的覆盖总方法数
$f(n-2)$	用 $2\times 1$ 的小矩形无重叠地覆盖一个 $2\times (n-2)$ 的大矩形的覆盖总方法数

情况一： 覆盖一个 $2\times n$ 的大矩形，若最后一个小矩形已经确定是竖着放的，那么覆盖该大矩形的覆盖总方法数就等于覆盖 $2\times (n-1)$ 的大矩形的覆盖总方法数。

情况二： 覆盖一个 $2\times n$ 的大矩形，若最后一个小矩形已经确定是横着放的，那么覆盖该大矩形的覆盖总方法数就等于覆盖 $2\times (n-2)$ 的大矩形的覆盖总方法数。

而实际覆盖 $2\times n$ 的大矩形时，我们并不知道最后一个小矩形是横着放还是竖着放，所以覆盖 $2\times n$ 的大矩形的覆盖总方法数应该是这两种情况的方法数之和，即$f(n)=f(n-1)+f(n-2)$。

当然，我们不能让这个公式一直往前推，总得给它一个尽头，很容易知道的就是$f(1)$和$f(2)$。

$f(1)$就是用 $2\times 1$ 的小矩形无重叠地覆盖一个 $2\times 1$ 的大矩形的覆盖总方法数，很明显只有一种覆盖方法。

$f(2)$就是用 $2\times 1$ 的小矩形无重叠地覆盖一个 $2\times 2$ 的大矩形的覆盖总方法数，很明显这时有两种覆盖方法。

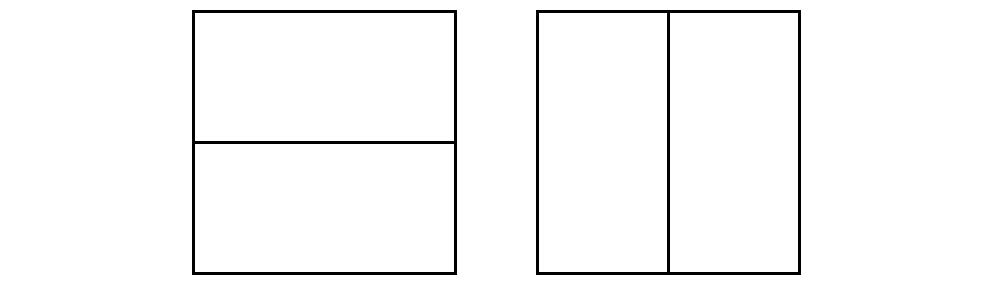
也就是说，$f(1)=1$，$f(2)=2$。

而当我们看到$f(n)=f(n-1)+f(n-2)$这个公式时，就应该知道这实际上就是一个斐波那契数列，我们直接使用斐波那契数列的最优解决方案进行代码编写即可。

//动规
class Solution {
public:
	int rectCover(int number) {
		if (number == 1 || number == 2) //f(1)=1, f(2)=2
			return number;
		int first = 1; //f(1)=1
		int second = 2; //f(2)=2
		int third = 0;
		while (number > 2) //进行number-2次计算
		{
			//f(n)=f(n-1)+f(n-2)
			third = first + second;
			first = second;
			second = third;
			number--;
		}
		return third;
	}
};