计算机视觉：图像分类-分类器及损失

Posted 2021-10-27 GeniusAng

1.CIFAR-10例子介绍

图像分类数据集示例：CIFAR-10，一个流行的图像分类数据集。这个数据集由60000个32像素高和宽组成的小图像组成。每个图像都被标记为10个类之一（例如“飞机、汽车、鸟等”）。这60000个图像被分割成50000个图像的训练集和10000个图像的测试集。在下图中，您可以看到10个类中每个类的10个随机示例图像：

上面图中就是数据集的类别和图像的示例，右边展示了一部分测试图像以及最相近的在训练集中前10张图片集合。

1.1算法思路

假设现在我们得到了cifar-10训练集，它包含50000个图像（每个标签有5000个图像），我们希望标记预测剩下的10000个图像。

• 最近邻分类器将得到一个测试图像，将其与每个训练图像进行比较，并预测其标签，为最近的训练图像的标签。

在上面和右边的图像中，您可以看到10个示例测试图像的这种过程的示例结果。注意，在大约10个示例中，只有3个检索到同一类的图像，而在其他7个示例中则不是这样。例如，在第8排，离马头最近的训练图像是一辆红色的汽车，大概是由于强烈的黑色背景。因此，在这种情况下，马的图像会被错误地标记为汽车。

如何比较图像两张图片
每个图像都是32 x 32 x 3的像素。最简单的方法之一是逐像素比较图像，并将所有差异相加。换句话说，给定两个图像并将其表示为向量 $I_1$，$I_2$，比较它们的合理选择可能是L1距离：
$$d_1(I_1,I_2)=\sum _p\left|I_1^p-I_2^p\right|$$

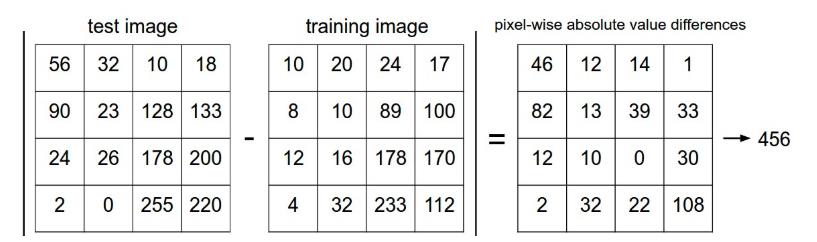
如果两个图像一样，结果为0，如果两个图像相差很大，结果会很大

训练数据集与测试数据L1距离代码实现：

distances = np.sum(np.abs(Xtrain - Xtest[i,:]), axis = 1)

设定输入的图片和标签形状为

Xtrain_rows = Xtrain.reshape(Xtrain.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000 x 3072
Xtest_rows = Xtest.reshape(Xtest.shape[0], 32 * 32 * 3) # Xte_rows becomes 10000 x 3072

完整代码实现(Numpy)

import numpy as np

class NearestNeighbor(object):
  def __init__(self):
    pass

  def train(self, X, y):
    """
    X：N x D形状，N为样本数，D为像素数量
    Y：1维，大小为N
    """
    # 所有最近邻需要的训练数据集
    self.Xtrain = X
    self.ytrain = y

  def predict(self, Xtest):
    """对输入的X若干个测试图片，每个进行预测"""
    num_test = Xtest.shape[0]
    # 确保输出类型一样
    Ypred = np.zeros(num_test, dtype = self.ytrain.dtype)

    # 循环所有测试数据
    for i in range(num_test):
      # 使用L1距离找到i最近的训练图片
      distances = np.sum(np.abs(self.Xtrain - Xtest[i,:]), axis = 1)
      min_index = np.argmin(distances)# 获取最近的距离的图像下标
      Ypred[i] = self.ytrain[min_index]# 预测标签（获取对应训练那张图片的目标标签）
    return Ypred

结果
使用上述方法，我们在CIFAR-10的测试机上面只能达到38.6% 的准确率，距离目前人类的测试结果（大概）94%的准确率，还有后面着重介绍的state of the art (SOTA，前沿的) 的卷积神经网络取得的效果95%

距离选择

距离有很多种方式，在计算两个向量的距离时候，也可以选择L2，欧式距离。
$$d_2(I_1,I_2)=\sqrt{\sum _p{\left(I_1^p-I_2^p\right)}^2}$$

只要去修改其中的距离计算即可

distances = np.sqrt(np.sum(np.square(Xtrain - Xtest[i,:]), axis = 1))

但是在实际的最近邻应用程序中，我们可以省略平方根操作，因为平方根是单调函数。缩放距离的绝对大小，因此有或没有顺序的最近邻是相同的。如果您使用L2距离在cifar-10上运行最近邻分类器，将获得35.4%的精度（略低于L1距离结果）。

L1和L2哪个好，没有明确的方法，具体问题具体分析，不断尝试

2.线性分类

现在，我们将开发一种功能更强大的图像分类方法，最终将其自然地扩展到整个神经网络和卷积神经网络。线性分类方法。这种方法来主要由两部分，一个函数将输入数据映射到一个类别分数，另一个就是损失函数来量化预测的分数与目标值之间的一致性。

回到CIFAR-10例子，输入训练图像的数据集50000张图片， 向量维度D = 32 x 32 x 3 = 3072像素，K大小为10个类别
$$x_i\in R^D,i=1$$

定义这样的函数为
$$\begin{gathered} f:R^D\mapsto R^K \\ f(x_i,W,b)=W{x}_i+b \end{gathered}$$

我们可以控制参数w，b的设置。我们的目标是设置这些参数，以便计算出的分数与整个训练集中的目标值标签相匹配。这种方法的一个优点是利用训练数据来学习参数w，b，但是一旦学习完成，我们就可以丢弃整个训练集，只保留学习到的参数。

2.1 线性分类解释

例子：为了方便看见，假设图像只有4个像素（4个单色像素，这里为了简单，不考虑3通道颜色），并且我们有3个类（猫（CAT）、狗（DOG）、轮船（SHIP）。我们将图像像素拉伸成一列，然后进行矩阵乘法得到每个类的分数。$y=Wx+b=[3,4]\ast [4,1]+[3,1]=[3,1]$。上图图中的权重计算结果结果并不好，权重会给我们的猫图像分配一个非常低的猫分数。得出的结果偏向于狗。

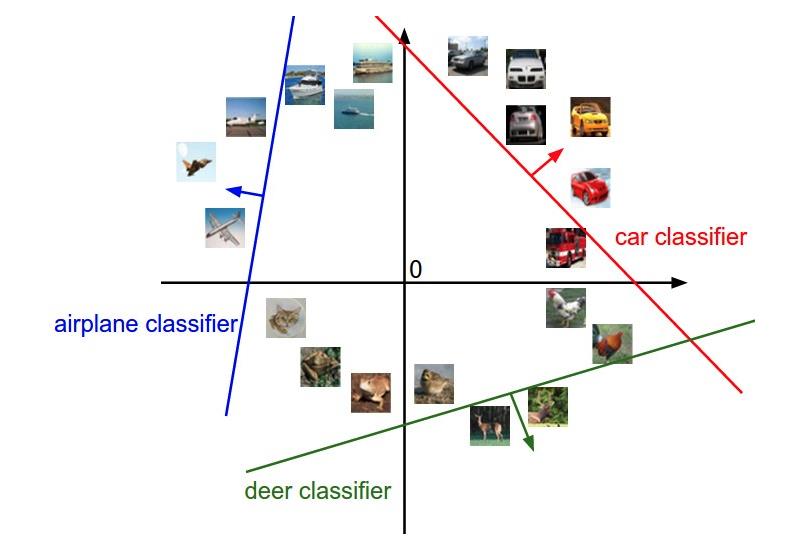
如果可视化分类，我们为了方便，将一个图片理解成一个二维的点，在下面坐标中显示如下：

• 解释：w的每一行都是其中一个类的分类器。这些数字的几何解释是，当我们改变w的一行时，像素空间中相应的线将以不同的方向旋转。而其中的偏置是为了让我们避免所有的分类器都过原点。

• 总结：分类器的权重矩阵其实是对应分类的经过训练得到的一个分类模板，通过测试数据与分类模板间的数据计算来进行分类。在训练的过程中，其实可以看作是权重矩阵的学习过程，也可以看成是分类模板的学习过程，如何从训练样本中学习分类的模板。模板权重的大小，反映了样本中每个像素点对分类的贡献率

学习到的权重

将线性分类器解释为模板匹配。权重w的另一种解释是，w的每一行对应于其中一个类的模板（有时也称为原型）。然后，通过使用内部积（或点积）逐个比较每个模板和图像来获得图像的每个类的分数，以找到“最适合”的模板。我们以CIFAR-10例子，10个类别分类，学习到10个模板，下方显示的即是训练过后所学习的权重矩阵（也即是分类模板）

线性分类器将数据中这两种模式的马合并到一个模板中。类似地，汽车分类器似乎已经将多个模式合并到一个模板中，该模板必须从各个方面识别所有颜色的汽车。特别是，这个模板最终是红色的，这意味着cifar-10数据集中的红色汽车比任何其他颜色的都多。线性分类器太弱，无法正确解释不同颜色的汽车，但正如我们稍后将看到的，神经网络将允许我们执行这项任务。

存在问题：

• 每个类别，只能学习到一个模板，分类能力是有限的，如果数据集中的图片同一类别差差异较大，那么学习不到太多的东西来进行判别。
• 无法进行非线性的分类（类似于异或的分类）[后面会介绍]

2.2 损失函数

损失函数是用来告诉我们当前分类器性能好坏的评价函数，是用于指导分类器权重调整的指导性函数，通过该函数可以知道该如何改进权重系数。CV与深度学习课程之前，大家应该都接触过一些损失函数了，例如解决二分类问题的逻辑回归中用到的对数似然损失、SVM中的合页损失等等。

• 对数似然损失
  $$L(y,\hat{y})=-y\log \hat{y}-(1-y)\log (1-\hat{y})$$
• 合页损失
  $$L_i=\sum _{j\ne y_i}\max (0,s_j-s_{y_i}+\Delta )$$

现在回到前面的线性分类例子，该函数预测在“猫”、“狗”和“船”类中的分数，我们发现，在这个例子中，我们输入描绘猫的像素，但是猫的分数与其他类别（狗的分数437.9和船的分数61.95）相比非常低（-96.8）。那么这个结果并不好，我们将会去衡量这样的一个成本，如果分类做好了，这个损失将会减少。

多分类问题的损失该如何去衡量？下面会进行通常会使用的两种方式作对比，这里介绍在图像识别中最常用的两个损失——多类别SVM损失（合页损失hinge loss）和交叉熵损失，分别对应多类别SVM分类器和Softmax分类器

2.2.1 多分类SVM损失

函数通过函数$f(x_i,W)$计算分数，我们在这里简写成$s$，对于某个$i$样本，某个$j$目标类别分数记做$s_j=f_j(x_i,W)$

得到：
$$L_i=j\ne y_i$$

计算机视觉框架OpenMMLab开源学习：图像分类实战

计算机视觉一个简单易上手的图像分类任务pipeline代码

AI遮天传 DL-深度学习在计算机视觉中的应用

计算机视觉常用算法讲解

计算机视觉（CV）基于高层API实现宝石分类