图--01---图的简介

Posted 2021-10-26 高高for 循环

文章目录

• 图的简介
• • 图的实际应用：
  • • 地图：
    • 电路图：
  • 图的定义
  • • • 定义：==图是由一组顶点和一组能够将两个顶点相连的边组成的==
    • 自环、平行边
  • 图的分类：
  • 图的相关术语
• 图的存储结构
• • 邻接矩阵
  • 邻接表
• 无向图的实现
• • API设计
  • 代码

---

图的简介

图的实际应用：

在现实生活中，有许多应用场景会包含很多点以及点点之间的连接，而这些应用场景我们都可以用即将要学习的图这种数据结构去解决。

地图：

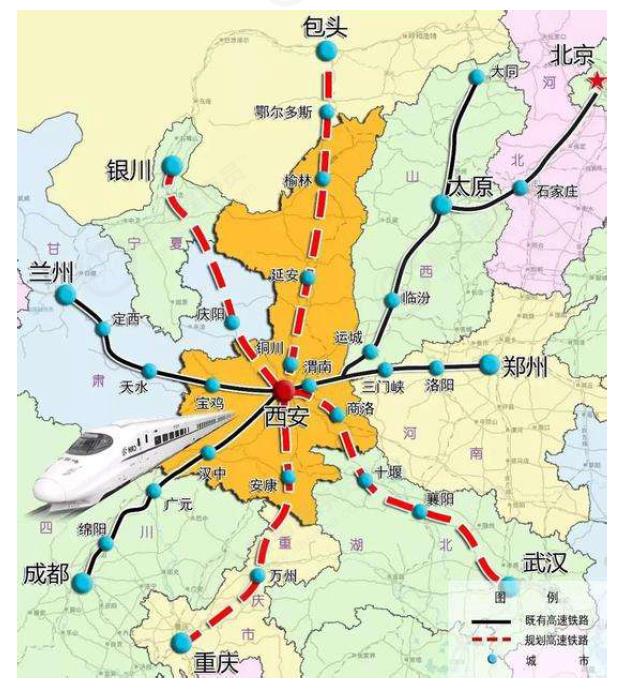
• 我们生活中经常使用的地图，基本上是由城市以及连接城市的道路组成，如果我们把城市看做是一个一个的点，把道路看做是一条一条的连接，那么地图就是我们将要学习的图这种数据结构。
  

电路图：

• 下面是一个我们生活中经常见到的集成电路板，它其实就是由一个一个触点组成，并把触点与触点之间通过线进行连接，这也是我们即将要学习的图这种数据结构的应用场景
  

图的定义

定义：图是由一组顶点和一组能够将两个顶点相连的边组成的

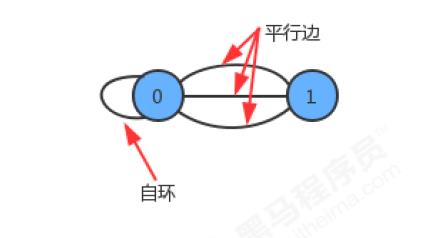
自环、平行边

1. 自环：即一条连接一个顶点和其自身的边；
2. 平行边：连接同一对顶点的两条边；
   

图的分类：

按照连接两个顶点的边的不同，可以把图分为以下两种：

• 无向图：边仅仅连接两个顶点，没有其他含义；
• 有向图：边不仅连接两个顶点，并且具有方向；

图的相关术语

• 相邻顶点：
  当两个顶点通过一条边相连时，我们称这两个顶点是相邻的，并且称这条边依附于这两个顶点。
• 度：
  某个顶点的度就是依附于该顶点的边的个数
• 子图：
  是一幅图的所有边的子集(包含这些边依附的顶点)组成的图；
• 路径：
  是由边顺序连接的一系列的顶点组成
• 环：
  是一条至少含有一条边且终点和起点相同的路径

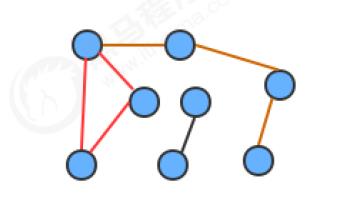
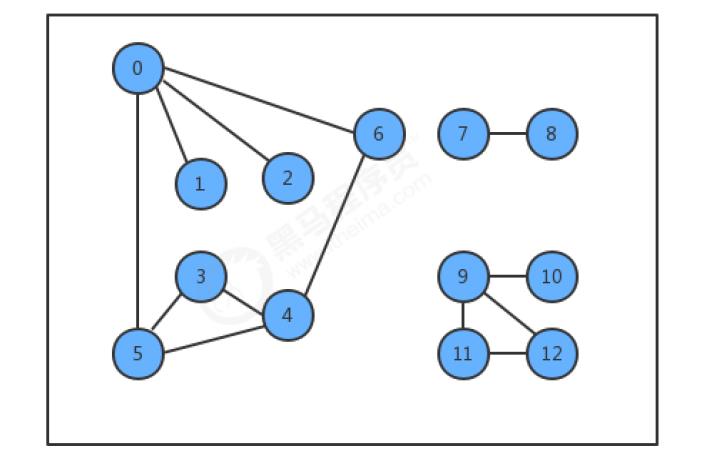
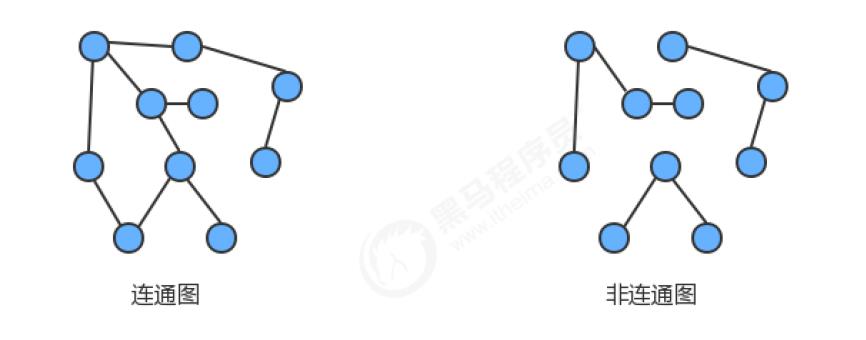
连通图：

• 如果图中任意一个顶点都存在一条路径到达另外一个顶点，那么这幅图就称之为连通图

连通子图：

• 一个非连通图由若干连通的部分组成，每一个连通的部分都可以称为该图的连通子图

图的存储结构

要表示一幅图，只需要表示清楚以下两部分内容即可：

1. 图中所有的顶点；
2. 所有连接顶点的边；

常见的图的存储结构有两种：邻接矩阵和邻接表

邻接矩阵

1. 使用一个V*V的二维数组int[V][V] adj,把索引的值看做是顶点；
2. 如果顶点v和顶点w相连，我们只需要将adj[v][w]和adj[w][v]的值设置为1,否则设置为0即可。

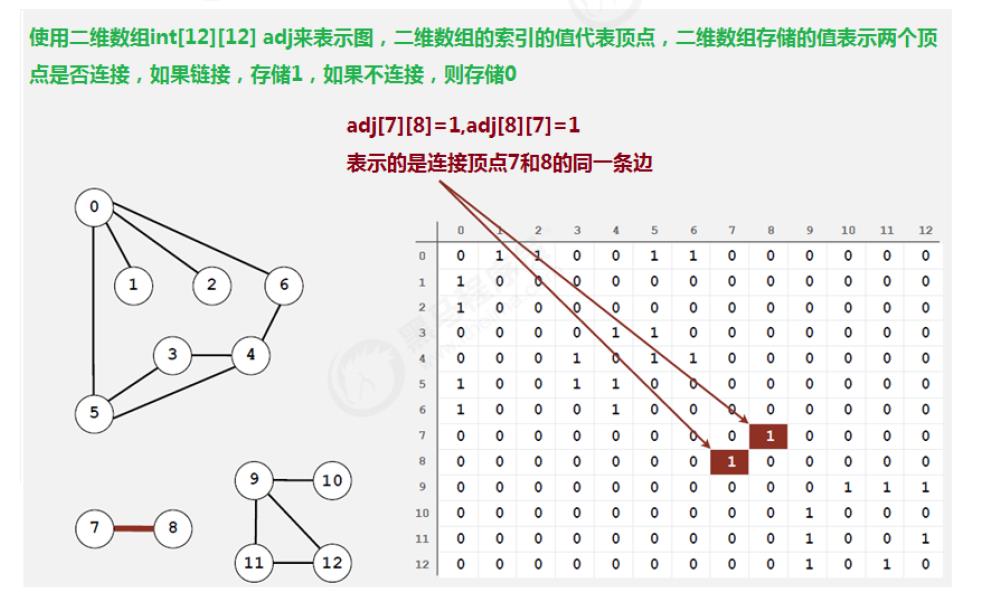
很明显，邻接矩阵这种存储方式的空间复杂度是V^2的，如果我们处理的问题规模比较大的话，内存空间极有可能不够用。

邻接表

1. 使用一个大小为V的数组 Queue[V] adj，把索引看做是顶点；
2. 每个索引处adj[v]存储了一个队列，该队列中存储的是所有与该顶点相邻的其他顶点
   
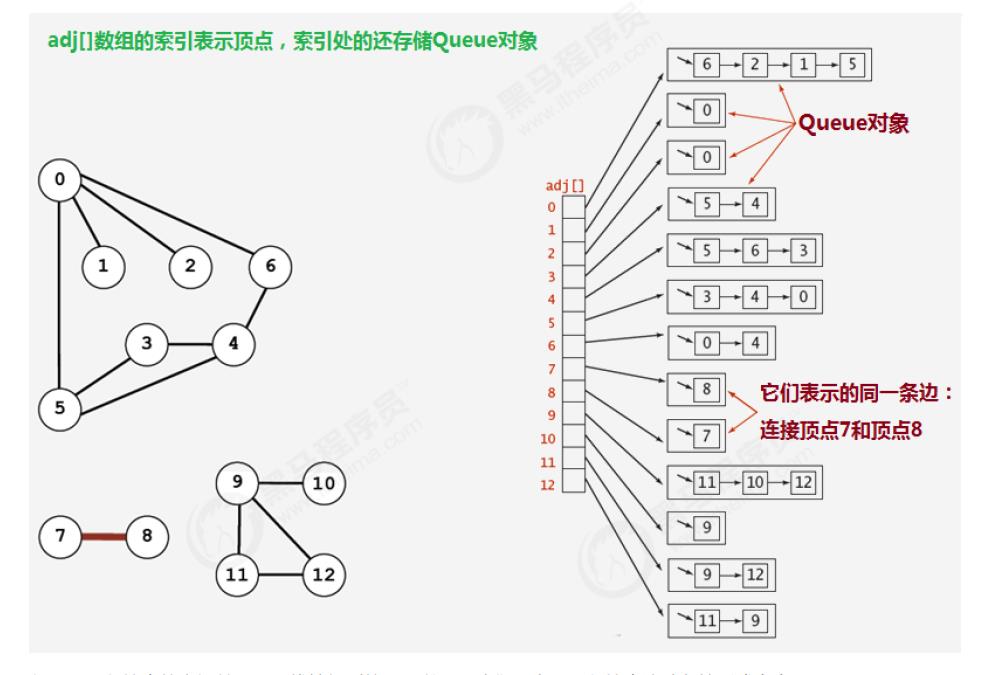
   很明显，邻接表的空间并不是是线性级别的，所以后面我们一直采用邻接表这种存储形式来表示图。

无向图的实现

API设计

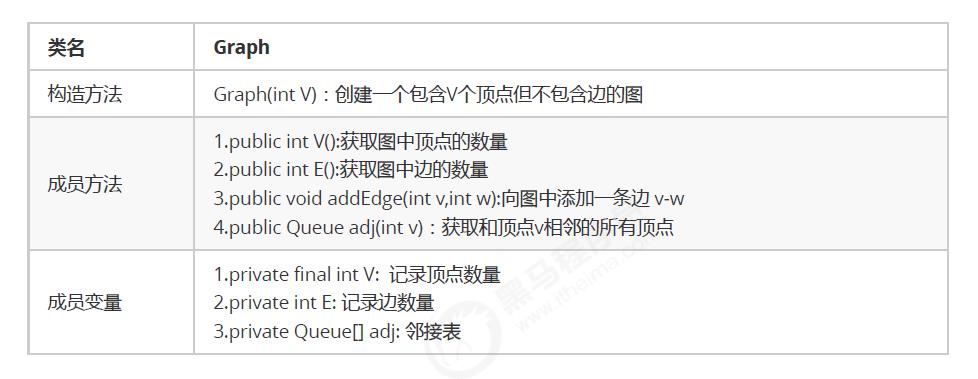
代码

package graph;

import java.util.Queue;
import java.util.concurrent.ConcurrentLinkedDeque;


public class Graph {
    //顶点数目
    private final int V;
    //边的数目
    private int E;
    //邻接表
    private Queue<Integer>[] adj;

    public Graph(int V){
        //初始化顶点数量
        this.V = V;
        //初始化边的数量
        this.E = 0;
        //初始化邻接表
        this.adj = new Queue[V];

        for (int i = 0; i < adj.length; i++) {
            adj[i] = new ConcurrentLinkedDeque<>();
        }
    }


    //获取顶点数目
    public int V(){
        return V;
    }

    //获取边的数目
    public int E(){
        return E;
    }

    //向图中添加一条边 v-w
    public void addEdge(int v, int w) {
        //在无向图中，边是没有方向的，所以该边既可以说是从v到w的边，又可以说是从w到v的边，因此，需要让w出现在v的邻接表中，并且还要让v出现在w的邻接表中

        adj[v].offer(w);
        adj[w].offer(v);
        //边的数量+1
        E++;

    }

    //获取和顶点v相邻的所有顶点
    public Queue<Integer> adj(int v){
        return adj[v];
    }

}