信号实验(03)连续时间系统的频域分析
Posted 揭航
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了信号实验(03)连续时间系统的频域分析相关的知识,希望对你有一定的参考价值。
信号实验(03)连续时间系统的频域分析
一.基础知识
1.1.数值积分
y=quadl('func', a, b)
% a、b 分别表示定积分的下限和上限
y=quadl(@myfun, a, b)
1.2.傅里叶变换和逆变换
% 要用到符号运算
fourier()
ifourier()
1.3.频率响应
freqs(b, a, w)
% b 为系统频率响应函数有理多项式中分子多项式的系数向量
% a 为分母多项式的系数向量,或微分方程左式的系数
% w 为需计算的系统频率响应的频率抽样点向量
二.例子
2.1.矩形信号
给定一个周期为 4、脉冲宽度为 2 的矩形信号,用 Matlab 计算其傅里叶
系数并绘图。(教材 p193,习题 4.7 第 a 小题)
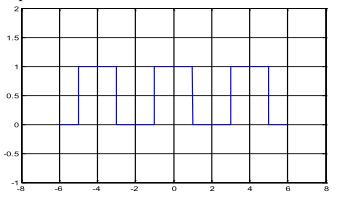
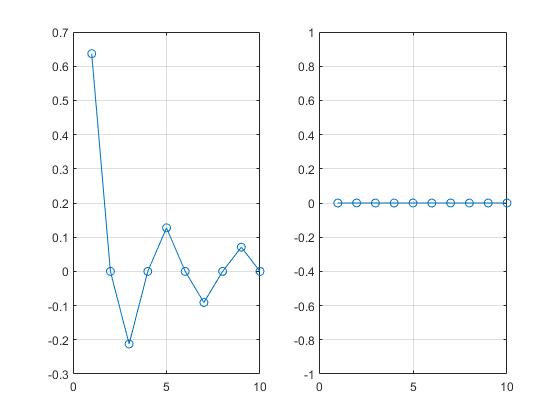
T = 4;
tao = 2;
w = 2 * pi / T;
a0 = quadl(@singrect, -2, 2) * 2 / T; % 计算 a0
N = 10;
an = zeros(1, N);
bn = zeros(1, N);
for k = 1:N
an(k) = quadl(@rectcos, -2, 2, [], [], k, w) * 2 / T;
% 计算 an. quadl 中的[], [] 表示以默认精度进行数值积分,k ,w 为
% rectcos 函数中的后两个参数;
bn(k) = quadl(@rectsin, -2, 2, [], [], k, w) * 2 / T; % 计算 bn;
end
n = 1:1:N;
figure(1);
subplot(1, 2, 1); plot(n, an, '-o'); grid on;
subplot(1, 2, 2); plot(n, bn, '-o'); grid on;
t = -6:0.01:6;
x = pulstran(t, -8:4:8, 'rectpuls', 2);
% 生成周期矩形脉冲信号
figure(2);
subplot(6, 2, 1);
plot(t, x);
axis([-8, 8, -1, 2]);
grid on;
% 有限项级数逼近
A0 = a0;
subplot(6, 2, 2);
plot(t, A0 / 2);
grid on; % 直流项
wave = a0 / 2;
for k = 1:10
wave = wave + an(k) * cos(k * w * t) + bn(k) * sin(k * w * t);
subplot(6, 2, k + 2);
plot(t, wave);
grid on;
end
2.2.门函数
给定一个宽度为 2 的门函数信号,用 Matlab 计算其傅里叶变换(教材p138,例题 4.4-1)及其性质并实现信号幅度调制。
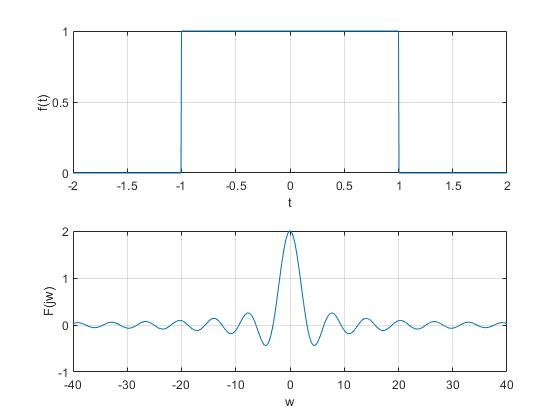
R = 0.005; t = -2:R:2;
%R 为时域采样间隔
f = (abs(t) <= 1);
% f 为时域
w1 = 40;
N = 1000;
k = -N:N;
w = k * w1 / N;
% w1 为角频率范围, N 为 为 采样点 数, ,w 为频率正半轴 采样点
F = f * exp(-j * t' * w) * R;
% 利用 向量内积相乘 ,求 求 F(jw), , 原理参见附录
% 求幅频特性
Fudu = real(F);
figure(1);
subplot(2, 1, 1);
plot(t, f);
xlabel('t');
ylabel('f(t)');
grid on;
subplot(2, 1, 2);
plot(w, Fudu);
xlabel('w');
ylabel('F(jw)');
grid on;
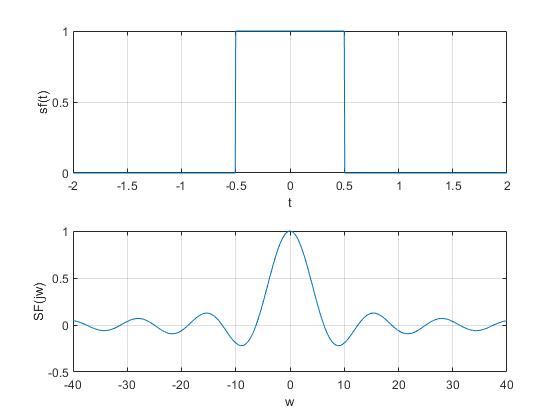
% 尺度变换
sf = (abs(t) <= 0.5); % sf 代表 f(2t)
w1 = 40; N = 1000;
k = -N:N;
w = k * w1 / N;
%w1 为角频率范围,为 采样点为 N ,w 为频率正半轴采样点
SF = sf * exp(-j * t' * w) * R;
% 利用 向量内积相乘 ,求 求 SF(jw). 原理参见附录
SFudu = real(SF); % 求幅频特性
figure(2);
subplot(2, 1, 1);
plot(t, sf);
xlabel('t');
ylabel('sf(t)');
grid on;
subplot(2, 1, 2);
plot(w, SFudu);
xlabel('w');
ylabel('SF(jw)');
grid on;
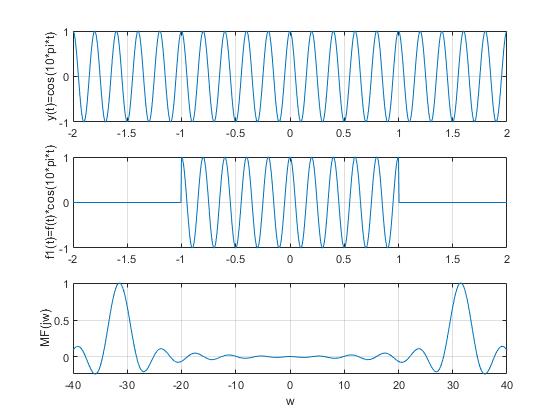
% 信号调制
mf = f .* cos(10 * pi * t); % mf 为已 调制 函数
figure(3);
subplot(3, 1, 1);
plot(t, cos(10 * pi * t)); % 绘制载波信号
ylabel('y(t)=cos(10*pi*t)');
grid on;
subplot(3, 1, 2);
plot(t, mf); % 绘制已 调制 信号
ylabel('f1(t)=f(t)*cos(10*pi*t)');
grid on;
MF = mf * exp(-j * t' * w) * R; % 求 求 已 调制谱 信号的频谱 F1(jw)
MFudu = real(MF); % 求 求 F1(jw) 的幅频特性
subplot(3, 1, 3);
plot(w, MFudu);
xlabel('w');
ylabel('MF(jw)');
grid on;
从上图可以看出,信号调制后其频谱分别向左和右搬移了 10 ,而其幅度
谱的形式并未改变
2.3.频率响应
给求下列微分方程所描述系统的频率响应
H
(
j
ω
)
H(j\\omega)
H(jω) ,并画出其幅频、相频
响应曲线:
y
′
′
(
t
)
+
5
y
′
(
t
)
+
6
y
(
t
)
=
f
′
(
t
)
+
4
f
(
t
)
y''(t)+5y'(t)+6y(t)=f'(t)+4f(t)
y′′(t)+5y′(t)+6y(t)=f′(t)+4f(t)
b = [1 4];
a = [1 5 6];
w = linspace(0, 5, 200);
H = freqs(b, a, w);
figure(1);
subplot(2, 1, 1);
plot(w, abs(H));
xlabel('\\omega');
ylabel('|H(j\\omega)|');
grid on;
subplot(2, 1, 2);
plot(w, angle(H));
xlabel('\\omega');
ylabel('\\phi');
grid on;

三.实验
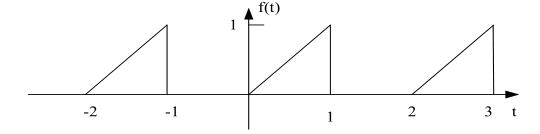
3.1.三角波傅里叶变换
周期性三角波如下图所示,计算其傅里叶级数系数,演示其有限项级数逼近并绘图。(教材 p193,习题 4.8 第 a 小题)
3.2.余弦函数傅里叶变换
3.3.三角波频谱
3.4.微分方程频率响应
四.思考题
-
在“实验内容与步骤”(1)中,采用三角函数和指数形式的的傅里叶分解有何不同,它们之间的关系是什么?采用不同项数的分解形式对原始函数进行逼近,效果有何不同?为什么?
-
综合考虑“实验内容与步骤”(2)和(3),比较傅氏变换时移和平移的不同效果。
以上是关于信号实验(03)连续时间系统的频域分析的主要内容,如果未能解决你的问题,请参考以下文章