GTSAM Tutorial学习笔记
Posted Jichao_Peng
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了GTSAM Tutorial学习笔记相关的知识，希望对你有一定的参考价值。
GTSAM Tutorial学习笔记
GTSAM Tutorial学习笔记
为了学习LIO-SAM，我快速过了一遍《机器人感知：因子图在SLAM中的应用》以及董靖大佬在泡泡机器人分享的《GTSAM Tutorial》，本博客内容主要是《GTSAM Tutorial》的学习笔记，并对GTSAM在LIO-SAM中的实际应用进行一些简单分析，如果对GTSAM有基本了解的同学可以直接跳到第三部分。
1. 基本原理
在下图是一个典型SLAM场景 以上是关于GTSAM Tutorial学习笔记的主要内容，如果未能解决你的问题，请参考以下文章 Python 2.7.8 学习笔记（001）python manuals/the python tutorial 深度学习 Deep LearningUFLDL 最新Tutorial 学习笔记 2：Logistic Regression Python 2.7.8 学习笔记（002）python manuals/the python tutorial -- 1. Whetting Your Appetite 深度学习 Deep Learning UFLDL 最新Tutorial 学习笔记 4：Debugging: Gradient Checking
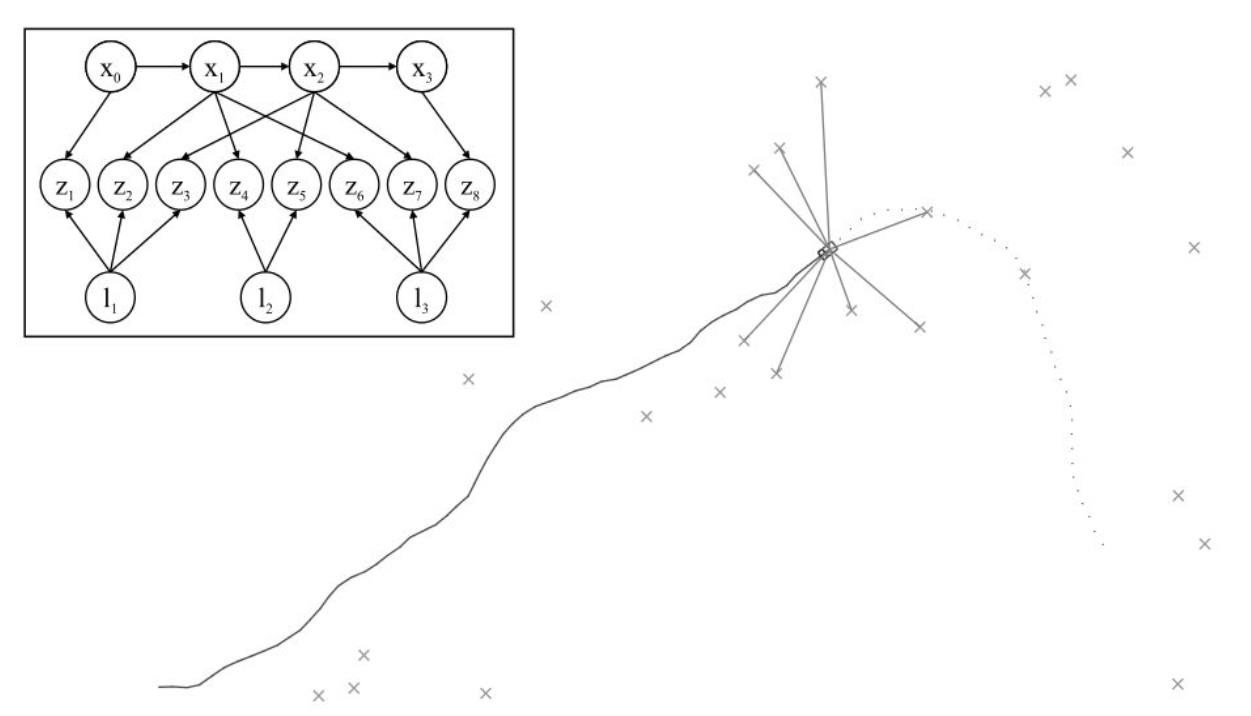
其中，机器人对特征点的观测可以构建为如上左图所示的一个贝叶斯网络，该贝叶斯网络中
x
i
x_i
xi为机器人状态，
z
i
z_i
zi为机器人观测值，
l
i
l_i
li为特征点。这样一个贝叶斯网络的联合分布概率可以通过如下公式表示：
P
(
X
,
L
,
Z
)
=
P
(
x
0
)
∏
i
=
1
M
P
(
x
i
∣
x
i
−
1
,
u
i
)
∏
k
=
1
K
P
(
z
k
∣
x
i
k
,
l
j
k
)
P(X, L, Z)=P\\left(x_{0}\\right) \\prod_{i=1}^{M} P\\left(x_{i} \\mid x_{i-1}, u_{i}\\right) \\prod_{k=1}^{K} P\\left(z_{k} \\mid x_{i_{k}}, l_{j_{k}}\\right)
P(X,L,Z)=P(x0)i=1∏MP(xi∣xi−1,ui)k=1∏KP(zk∣xik,ljk)其中，
P
(
x
0
)
P\\left(x_{0}\\right)
P(x0)为先验状态概率分布，
P
(
x
i
∣
x
i
−
1
,
u
i
)
P\\left(x_{i} \\mid x_{i-1}, u_{i}\\right)
P(xi∣xi−1,ui)表示已知状态
x
i
−
1
x_{i-1}
xi−1和控制量
u
i
u_{i}
ui分布的情况下，
x
i
\\boldsymbol{x}_{i}
xi的概率分布，具体为：
x
i
=
f
i
(
x
i
−
1
,
u
i
)
+
w
i
⇔
x_{i}=f_{i}\\left(x_{i-1}, u_{i}\\right)+w_{i} \\quad \\Leftrightarrow
xi=fi(xi−1,ui)+wi⇔
P
(
x
i
∣
x
i
−
1
,
u
i
)
∝
exp
−
1
2
∥
f
i
(
x
i
−
1
,
u
i
)
−
x
i
∥
Λ
i
2
P\\left(x_{i} \\mid x_{i-1}, u_{i}\\right) \\propto \\exp -\\frac{1}{2}\\left\\|f_{i}\\left(x_{i-1}, u_{i}\\right)-x_{i}\\right\\|_{\\Lambda_{i}}^{2}
P(xi∣xi−1,ui)∝exp−21∥fi(xi−1,ui)−xi∥Λi2
P
(
z
k
∣
x
i
k
,
l
j
k
)
P\\left(z_{k} \\mid x_{i_{k}}, l_{j_{k}}\\right)
P(zk∣xik,ljk)标示已知状态
x
i
k
\\boldsymbol{x}_{i_{k}}
xik和
l
j
k
l_{j_{k}}
ljk的分布的情况下，
z
k
z_{k}
zk的概率分布，具体为：
z
k
=
h
k
(
x
i
k
,
l
j
k
)
+
v
k
⇔
z_{k}=h_{k}\\left(x_{i_{k}}, l_{j_{k}}\\right)+v_{k} \\quad \\Leftrightarrow
zk=hk(xik,ljk)+vk⇔
P
(
z
k
∣
x
i
k
,
l
j
k
)
∝
exp
−
1
2
∥
h
k
(
x
i
k
,
l
j
k
)
−
z
k
∥
Σ
k
2
P\\left(z_{k} \\mid x_{i_{k}}, l_{j_{k}}\\right) \\propto \\exp -\\frac{1}{2}\\left\\|h_{k}\\left(x_{i_{k}}, l_{j_{k}}\\right)-z_{k}\\right\\|_{\\Sigma_{k}}^{2}
P(zk∣xik,ljk)∝exp−21∥hk(