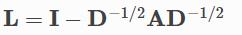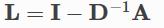torch_geometric 笔记：nn.ChebNet

Posted 2021-10-26 UQI-LIUWJ

1 理论部分

 

交通预测论文翻译：Deep Learning on Traffic Prediction: Methods,Analysis and Future Directions_UQI-LIUWJ的博客-CSDN博客-4.1.2.1.1 ChebNet

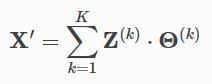
2  类写法

CLASSChebConv(
    in_channels: int, 
    out_channels: int, 
    K: int, 
    normalization: Optional[str] = 'sym', 
    bias: bool = True, 
    **kwargs)

3 参数说明

in_channels (int)	输入样本的通道数
out_channels (int)	输出样本的通道数 （在Cheb的源码中，每一阶切比雪夫多项式 进行卷积之后，都会再过一个FC，这个就是给每一阶的切比雪夫多项式卷积 修改维度、调整权重用的）
K (int)	几阶切比雪夫多项式近似
normalization (str, optional)	图拉普拉斯矩阵的归一化方法：默认是sym None 没有归一化        "sym" 对称归一化         "rw" 随机游走归一化     需要将lambda_max参数提供给forward()方法，以防normalization是不对称的 lambda_max 需要时一个[batch_size]维度的Tensor 可以使用torch_geometric.transforms.LaplacianLambdaMax 方法事先计算lambda_max
bias	默认是True ，如果是False，那么这个ChebNet就不会有偏移量

4 forward 函数

forward(
    x,
    edge_index, 
    edge_weight: Optional[torch.Tensor] = None, 
    batch: Optional[torch.Tensor] = None, 
    lambda_max: Optional[torch.Tensor] = None)

注：这里的batch是指torch_geometric笔记：数据集 ENZYMES &Minibatches_UQI-LIUWJ的博客-CSDN博客 第2小节中说的batch

5 源码

这里处理得很高妙，它相当于把正则化拉普拉斯矩阵作为新图的邻接矩阵

from typing import Optional
from torch_geometric.typing import OptTensor

import torch
from torch.nn import Parameter

from torch_geometric.nn.inits import zeros
from torch_geometric.utils import get_laplacian
from torch_geometric.nn.dense.linear import Linear
from torch_geometric.nn.conv import MessagePassing
from torch_geometric.utils import remove_self_loops, add_self_loops


class ChebConv(MessagePassing):
    def __init__(self, in_channels: int, out_channels: int, K: int,
                 normalization: Optional[str] = 'sym', bias: bool = True,
                 **kwargs):
        kwargs.setdefault('aggr', 'add')
        super(ChebConv, self).__init__(**kwargs)
        #设置聚合方式（add，也就是将各层切比雪夫多项式近似求和）

        assert K > 0
        assert normalization in [None, 'sym', 'rw'], 'Invalid normalization'
        #两个断言，切比雪夫多项式近似的阶数大于0；在这三种normalization里面选择

        self.in_channels = in_channels
        self.out_channels = out_channels
        self.normalization = normalization
        self.lins = torch.nn.ModuleList([
            Linear(in_channels, out_channels, bias=False,
                   weight_initializer='glorot') for _ in range(K)
        ])
        #各层切比雪夫多项式近似之后接的维度转换全连接层

        if bias:
            self.bias = Parameter(torch.Tensor(out_channels))
        else:
            self.register_parameter('bias', None)

        self.reset_parameters()

    def reset_parameters(self):
        #初始化参数
        for lin in self.lins:
            lin.reset_parameters()
        zeros(self.bias)


    def __norm__(self, edge_index, num_nodes: Optional[int],
                 edge_weight: OptTensor, normalization: Optional[str],
                 lambda_max, dtype: Optional[int] = None,
                 batch: OptTensor = None):
        #这里处理得很高妙，它相当于把正则化拉普拉斯矩阵作为新图的邻接矩阵

        edge_index, edge_weight = remove_self_loops(edge_index, edge_weight)
        #去掉自环

        edge_index, edge_weight = get_laplacian(edge_index, edge_weight,
                                                normalization, dtype,
                                                num_nodes)
        #计算拉普拉斯矩阵

        if batch is not None and lambda_max.numel() > 1:
            lambda_max = lambda_max[batch[edge_index[0]]]

        edge_weight = (2.0 * edge_weight) / lambda_max
        edge_weight.masked_fill_(edge_weight == float('inf'), 0)
        #图中所有原来边权重非零的边，权重全部乘以2/lambda_max

        edge_index, edge_weight = add_self_loops(edge_index, edge_weight,
                                                 fill_value=-1.,
                                                 num_nodes=num_nodes)
        #由于归一化拉普拉斯矩阵还需要-I，所以所有的自环权重减一
        assert edge_weight is not None

        return edge_index, edge_weight
        #返回以拉普拉斯矩阵为邻接矩阵的“新图”

    def forward(self, x, edge_index, edge_weight: OptTensor = None,
                batch: OptTensor = None, lambda_max: OptTensor = None):
        """"""
        if self.normalization != 'sym' and lambda_max is None:
            raise ValueError('You need to pass `lambda_max` to `forward() in`'
                             'case the normalization is non-symmetric.')

        if lambda_max is None:
            lambda_max = torch.tensor(2.0, dtype=x.dtype, device=x.device)
        if not isinstance(lambda_max, torch.Tensor):
            lambda_max = torch.tensor(lambda_max, dtype=x.dtype,
                                      device=x.device)
        assert lambda_max is not None

        edge_index, norm = self.__norm__(edge_index, x.size(self.node_dim),
                                         edge_weight, self.normalization,
                                         lambda_max, dtype=x.dtype,
                                         batch=batch)
        #得到以拉普拉斯矩阵为邻接矩阵的“新图”

        Tx_0 = x
        #Z_1=X
        out = self.lins[0](Tx_0)

        # propagate_type: (x: Tensor, norm: Tensor)
        if len(self.lins) > 1:
            Tx_1 = self.propagate(edge_index, x=x, norm=norm, size=None)
            #每一轮的propagate相当于对每个点，计算所有邻边的拉普拉斯矩阵权重*临近点,再求和【aggr=add】
            out = out + self.lins[1](Tx_1)
            #Z_2=LX

        for lin in self.lins[2:]:
            Tx_2 = self.propagate(edge_index, x=Tx_1, norm=norm, size=None)
            #Tx_2=Z_k=L*Z_k-1
            Tx_2 = 2. * Tx_2 - Tx_0
            #Z_k=2*L*k-1-Z_k-2
            out = out + lin.forward(Tx_2)
            Tx_0, Tx_1 = Tx_1, Tx_2

        if self.bias is not None:
            out += self.bias

        return out


    def message(self, x_j, norm):
        return norm.view(-1, 1) * x_j
        #就是对应的邻边权重*邻接点

    def __repr__(self):
        return '{}({}, {}, K={}, normalization={})'.format(
            self.__class__.__name__, self.in_channels, self.out_channels,
            len(self.lins), self.normalization)

6 举例

from torch_geometric.nn import ChebConv

data
#Batch(x=[9893, 1], edge_index=[2, 34637], y=[9893, 1], batch=[9893], ptr=[2])

conv1 = ChebConv(1, 32, 2)

x = conv1(data.x, data.edge_index)

type(x)
#torch.Tensor

x.shape
#torch.Size([9893, 32]) 每个点的维度是[9893,32]