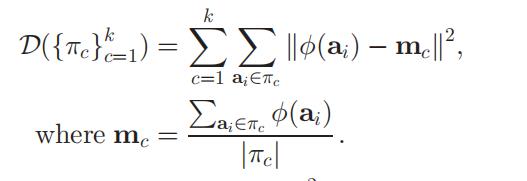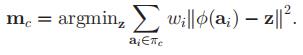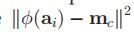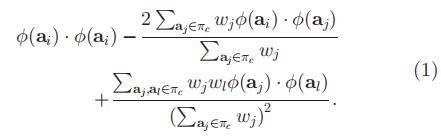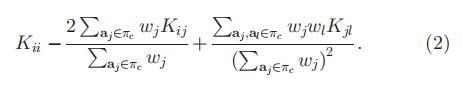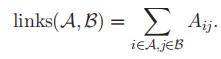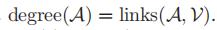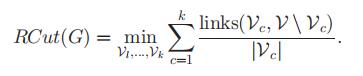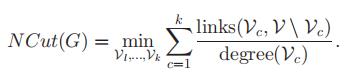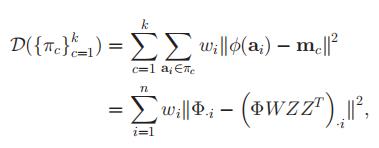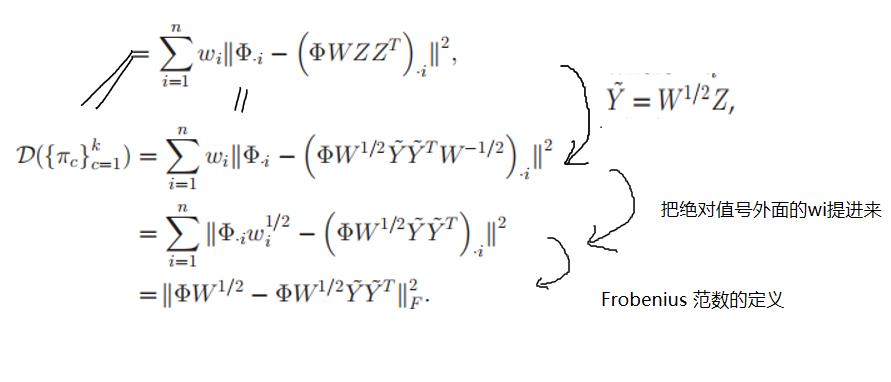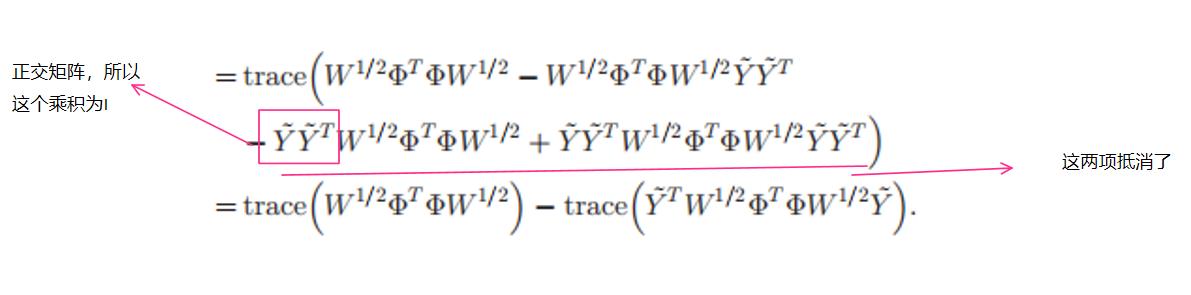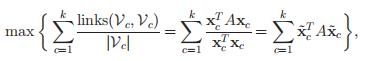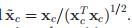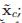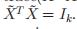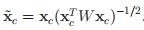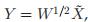论文笔记：Weighted Graph Cuts without Eigenvectors:A Multilevel Approach

Posted 2021-10-26 UQI-LIUWJ

1 introduction

        在本文中，我们讨论了两种看似不同的方法对非线性可分数据的聚类:核k均值和谱聚类之间的等价性。

        利用这种等价性，我们设计了一种基于核的快速multigraph聚类算法，该算法在速度、内存使用和质量方面都优于谱聚类方法。

        核k-means算法是标准k-means算法的推广。通过隐式地将数据映射到高维空间，核k-means可以发现输入空间中非线性可分的聚类

        最近，由于特征向量，频谱聚类（spectral clustering）在各种机器学习任务[7]中得到了广泛的应用。

         在本文中，我们将得到，核k-means的加权形式在数学上等价于一般加权图的聚类问题。

        这种等价性有一个直接的含义:我们可以使用加权核k均值算法局部优化一些图聚类目标，反之，也可以使用谱方法对加权核k均值进行优化。

        在特征向量计算难以求得的情况下(例如，如果一个非常大的矩阵需要许多特征向量)，加权核k均值算法可能比谱方法更可取。

A,X,φ等大写字母	矩阵
a,b等小写字母	向量
V,E	集合
||a||	a的L2范数
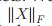	X的Frobenius 范数 线性代数笔记：Frobenius 范数_UQI-LIUWJ的博客-CSDN博客

 

 2 核K-Means

K-means：

        给定向量，K-means的目的是为了找到k个集簇。使得目标函数最小

 核k-means

先使用函数Φ来讲数据点映射到高维特征空间中，然后在那个空间中使用K-means

 目标函数可以改写成：

  

距离可以写成

=

在这种情况下，距离只需要 内积操作就可以实现了。

因此，给定一个核矩阵K（），和的距离可以在不知道这两个的具体高维表示的情况下得到

任何一个半正定矩阵K可以被视为是核矩阵 

 

 常见的核函数

 

 2.1 加权核K-means

         现在我们引入一个加权版本的核k-means目标函数正如我们稍后将看到的，权值在显示与图聚类的等价性方面起着至关重要的作用。

 

注：权重非负

        m是“最好的”集簇代表（这一个集簇内任何别的点当这个集簇代表，这个集簇加权距离之和都大于m作为集簇代表求出来的值） 

 和之前一样，我们计算一下

 =

 

 使用核矩阵K，我们可以有：

 3 图划分

 我们记表示点集A和点集B之间的边的权重之和

记点集A的度为A和整张图的点集V之间的link 

 

 图划分问题旨在将将图划分成k个独立的部分V1....Vk，他们的并集是V

几种典型的图划分方法 

Ratio association.	最大化类内link
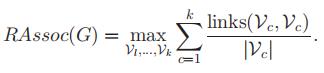
ratio cut	最小化类与类外点之间的link
Kernighan-Lin objective	和ratio cut很类似，唯一的不同是，这里要求各个分割的图节点数一样
Normalized cut	也和ratio cut类似，不同之处在于，相比于Kernighan-Lin objective，这里不是用点的数量，而是用度数进行的归一化

一个结论：

 3.1 加权的图割

我们记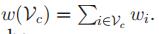

类比 ratio association （ratio association 是一种特殊情况：所有的点权重都是1）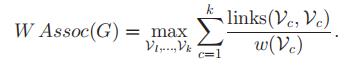
类比 ratio cut （ratio cut 是一种特殊情况：所有的点权重都是1）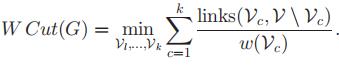

 4 二者的联系

        乍一看，前两节中介绍的两种clustering方法似乎是不相关的。

        在本节中，我们首先将加权核k均值目标表示为一个迹最大化问题。

        然后我们将加权图关联和图切割问题也改写为矩阵迹最大化，从而证明这两个目标在数学上是等价的。

        最后，我们讨论了与谱方法的联系，并展示了如何加强邻接矩阵的正定性，以保证加权核k-均值算法的收敛性。

 4.1 加权核k-means ——> 迹最大化 Trace Maximization

我们记：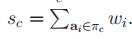

同时我们定义一个N*K的矩阵

 

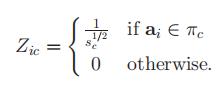
 很显然Z的列向量互相正交，因为他们捕获的是独立的几个簇的点。

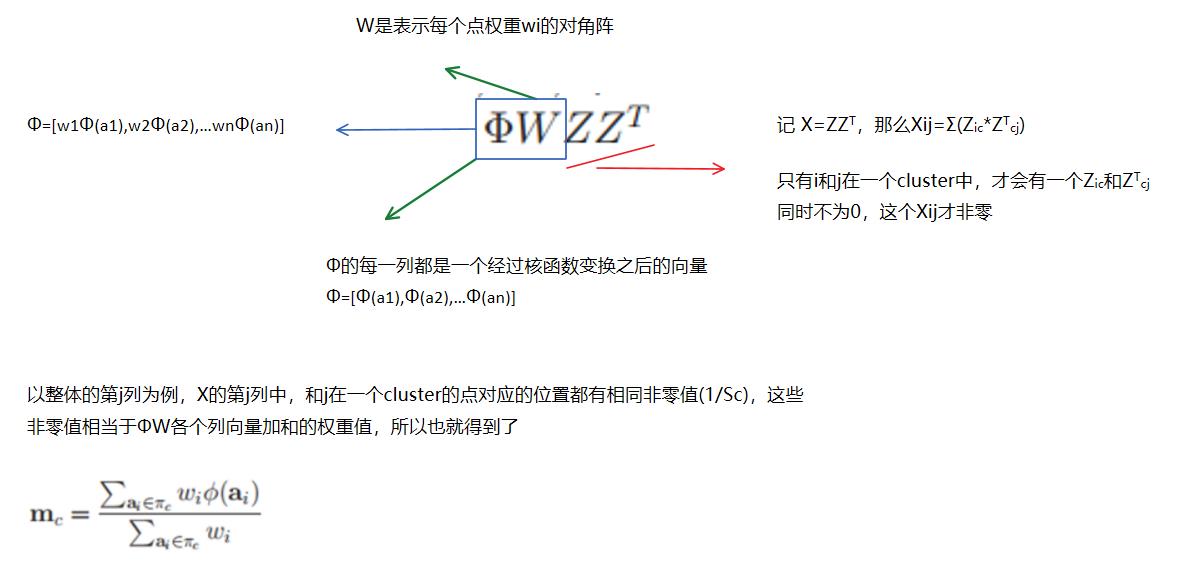
假设Φ表示所有向量组成的矩阵，W是表示每个点权重wi的对角阵

 

那么矩阵的第i列表示包含ai的那个集簇的平均向量

即 =

 解释一下：

于是，加权 核K-means可以写成

其中表示矩阵Φ的第i列。

 令不难发现是一个正交矩阵（）

因此

 

 而我们又知道  :

• trace(AB)=trace(BA)
•  
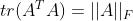
• trace(A+B)=trace(A)+trace(B)

所以我们可以重新写

 ​​​​​​

而K= ，

对同一张图，是固定值

 所以我们加权核k-means的目标函数相当于

 

 .4.2 Ratio association ——> 迹最大化 Trace Maximization

 我们引入一个指示函数 Xc。Xc(i)=1表示类别包括了节点i。

于是我们可以把原来的式子：

 改写成

         只有i，j都是在c这个类中，才会有一项正数加进去，所以 这个式子加上去的都是在c这个类中的点之间的边权重

 可以看成，其中的第c列是

 很显然

 当所有的点权重是1的时候，可以很容易地发现，这里的和前面的是一样的

 在W=I的情况下，如果K=A，那么两个的目标函数是一样的

    VS  

 4.3 weighted Ratio association

 

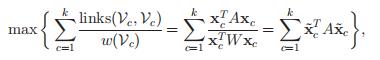
这里 

 和4.1一样，我们令

 于是有：

 

4.4 两个问题的互通

4.4.1 weighted graph——>weighted K-means

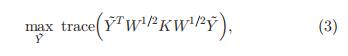
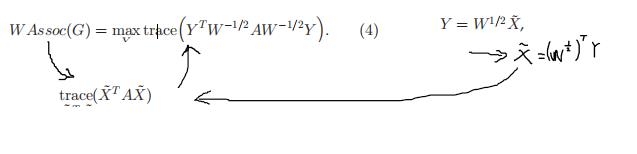
 我们可以发现（4）式的Y和（3）式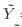的是一样的

同时我们令（3）式的K=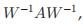，那么两个式子的目标函数就一样了

4.4.2  weighted K-means ——> weighted graph

 给定核矩阵K，以及每个点的权重矩阵K，我们令A=WKW，以A为邻接矩阵构造一个图，就可以了