CF1149B Three Religions

Posted 2021-10-25 Jozky86

CF1149B Three Religions

题意：

给定长度为 n 的母串和三个子串$s_1,s_2,s_3$ 。初始时子串均为空。有 q 次询问。你需要支持两种操作：向某个子串末尾添加一个字母，或者删去某个子串末尾的字母。在每次操作后，你需要回答，是否能从母串中分离出三个不相交的子序列（不改变字符原有顺序），满足这三个子序列恰好是$s_1,s_2,s_3$
在任意时刻,$s_1,s_2,s_3$的长度均不会超过 250

$1\le n\le 10^5,1\le q\le 10^3$

题解：

想了半天，想不到真的想不到啊
dp题
设f[i][j][k]:表示匹配了A串的前i个字符(第i个字符选择了原串中x位置)，B串匹配了前j个字符(第j个字符选择原串中y位置)，C串匹配了前k个字符时(选择原串中z位置)，至少需要到模式串的位置(max(x,y,z))
数组s[i][0/1/2]:分别表示三个子串s1,s2,s3
我们需要一个nxt[i][c]来辅助转移：表示在原串中[i,n]区间内，'c’字符第一次出现的位置
对着图，nxt数组的含义很好理解。cf官方题解的图

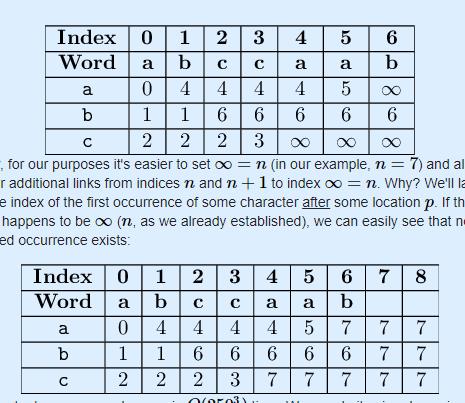
现在我们开始考虑转移：
当f[][][]>n时就说明匹配失败
初始化f[i][j][k]=n+1,f[0][0][0]=0
转移方程：
f [ i ] [ j ] [ k ] = m i n { n x t [ f [ i − 1 ] [ j ] [ k ] + 1 ] [ s [ 1 ] [ i ] ] , n x t [ f [ i ] [ j − 1 ] [ k ] + 1 ] [ s [ 2 ] [ j ] ] ， n x t [ f [ i ] [ j ] [ k − 1 ] + 1 ] [ s [ 3 ] [ k ] ] } f[i][j][k]=min\\{nxt[f[i-1][j][k]+1][s[1][i]],nxt[f[i][j-1][k]+1][s[2][j]]，nxt[f[i][j][k-1]+1][s[3][k]]\\} f[i][j][k]=min{nxt[f[i−1][j][k]+1][s[1][i]],nxt[f[i][j−1][k]+1][s[2][j]]，nxt[f[i][j][k−1]+1][s[3][k]]}
其实含义很简单：我们就试图从A串中加个字符找后续位置，从B串中价格字符找后续位置，从C串中价格字符找后续位置，从这个三个位置中选取最佳(即最左边)转移
对于每次插入我们只会在一个子串末端加，另外两个不变，那么新增状态只有新加字符与另外两个不变的串的位置关系，这样有$1\ast 250\ast 250$种状态，对于这些新状态重新跑就可以，不用全部都重新跑
对于删除操作，直接减小对应串长。因为我们之前转移时小的状态都算好了，所以直接减对应的串长就可以得到新的答案
答案就是$ans[f[len1][len2][len3]]$,表示三个串全部匹配完之后，在模式串中的最左点。对于样例来说，就是如图三个位置取最大值。如果<=n，说明有解，如果>n，说明无解

代码：

#include <bits/stdc++.h>
#include <unordered_map>
#define debug(a, b) printf("%s = %d\\n", a, b);
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
clock_t startTime, endTime;
//Fe~Jozky
const ll INF_ll= 1e18;
const int INF_int= 0x3f3f3f3f;
void read(){};
template <typename _Tp, typename... _Tps> void read(_Tp& x, _Tps&... Ar)
{
    x= 0;
    char c= getchar();
    bool flag= 0;
    while (c < '0' || c > '9')
        flag|= (c == '-'), c= getchar();
    while (c >= '0' && c <= '9')
        x= (x << 3) + (x << 1) + (c ^ 48), c= getchar();
    if (flag)
        x= -x;
    read(Ar...);
}
template <typename T> inline void write(T x)
{
    if (x < 0) {
        x= ~(x - 1);
        putchar('-');
    }
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
void rd_test()
{
#ifdef ONLINE_JUDGE
#else
    startTime = clock ();
    freopen("data.in", "r", stdin);
#endif
}
void Time_test()
{
#ifdef ONLINE_JUDGE
#else
    endTime= clock();
    printf("\\nRun Time:%lfs\\n", (double)(endTime - startTime) / CLOCKS_PER_SEC);
#endif
}
const int maxn=2e5+9;
int s[4][300];
int nxt[maxn][30];
int f[300][300][300];
int len[4];
int n,q;
char str[maxn];
void init(){
	for(int i=0;i<26;i++)nxt[n+1][i]=nxt[n+2][i]=n+1;
	for(int i=n;i;i--){
		for(int j=0;j<26;j++){
			if(str[i]==j+'a')nxt[i][j]=i;
			else nxt[i][j]=nxt[i+1][j];
		}
	}
}
void solve(){
	char ch;
	cin>>ch;
	int id;
	read(id);
	if(ch=='+'){
		cin>>ch;
		s[id][++len[id]]=ch-'a';
		for(int i=(id==1?len[1]:0);i<=len[1];i++){
			for(int j=(id==2?len[2]:0);j<=len[2];j++){
				for(int k=(id==3?len[3]:0);k<=len[3];k++){
					int now=n+1;
					if(i)now=min(now,nxt[f[i-1][j][k]+1][s[1][i]]);
					if(j)now=min(now,nxt[f[i][j-1][k]+1][s[2][j]]);
					if(k)now=min(now,nxt[f[i][j][k-1]+1][s[3][k]]);
					f[i][j][k]=now;
				}
			}
		}
	}
	else if(ch=='-')
	{
		len[id]--;
	}
	cout<<"f[][][]="<<f[len[1]][len[2]][len[3]]<<endl;
	if(f[len[1]][len[2]][len[3]]<=n)puts("YES");
	else puts("NO");
}
int main()
{
    //rd_test();
	read(n,q);
	scanf("%s",str+1);
	init();
	while(q--)solve();
	return 0;
    //Time_test();
}