CS224W摘要13.Community Detection in Networks
Posted oldmao_2000
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了CS224W摘要13.Community Detection in Networks相关的知识,希望对你有一定的参考价值。
文章目录
CS224W: Machine Learning with Graphs
公式输入请参考: 在线Latex公式
Community Detection in Networks
先看结论:
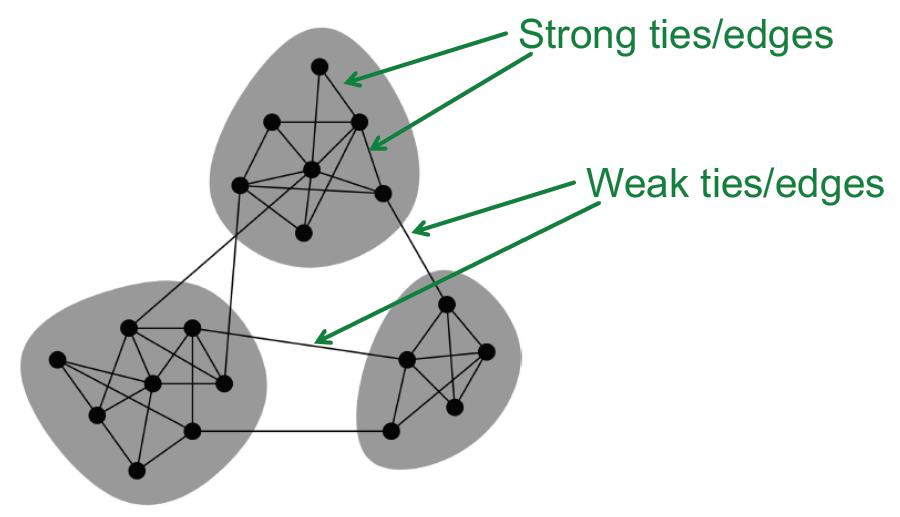
网络中会存在聚集的Community,其内部关系是strong relation,各个Community之间存在weak relation。
Social network视角下的图
在社交网络中,可以把人看做节点,人与人的关系看做边,由于人的关系疏密不一致,可以分成两种,而在边上传递着各种信息流:
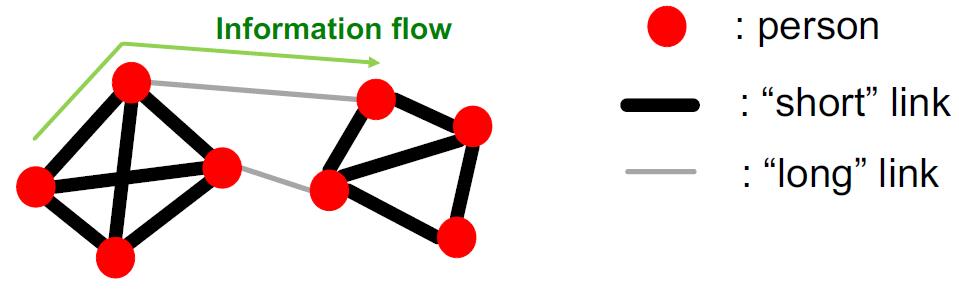
例如,Mark Granovetter在1960年代的博士研究中发现,社交网络中人获取信息的方式不是通过周围的好友,往往是通过一些熟人的方式来获取,例如:同事等。
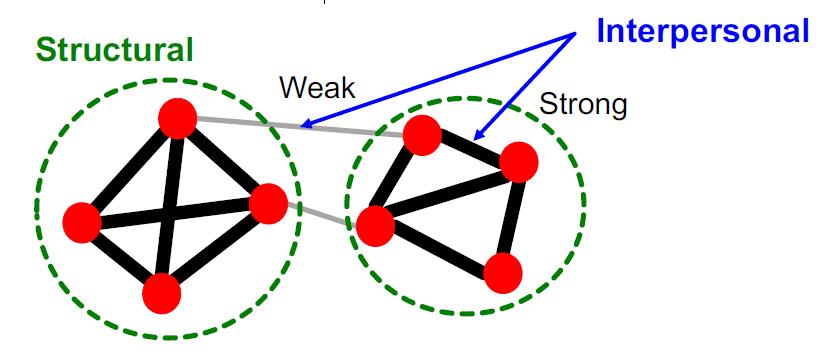
这个现象出现的原因在于friendships的两个方面:
- Structural: Friendships span different parts of the network.
§ Structurally embedded (tightly-connected) edges are also socially strong
§ Long-range edges spanning different parts of the network are socially weak - Interpersonal: Friendship between two people is either strong or weak
当前comunity中的信息往往都是已知的(冗余redundant),从comunity之间的long-range边才能获取更多不同信息,从而帮助当前节点解决问题,例如找工作。
Triadic Closure
Triadic Closure是指在社交网络中,节点往往有三角形的relation关系。
If 𝑩 and 𝑪 have a friend 𝑨 in common, then:
𝑩 is more likely to meet 𝑪
§ (since they both spend time with 𝑨)
𝑩 and 𝑪 trust each other
§ (since they have a friend in common)
𝑨 has incentive to bring 𝑩 and 𝑪 together
§ (since it is hard for 𝑨 to maintain two disjoint relationships)
有研究表明,青少年女生low clustering coefficient,那么suicide倾向较高。
人类就是群居动物。
Edge overlap
下面来看如何量化两个节点间关系的强弱:
O
i
j
=
∣
(
N
(
i
)
∩
N
(
j
)
)
−
{
i
,
j
}
∣
∣
(
N
(
i
)
∪
N
(
j
)
)
−
{
i
,
j
}
∣
O_{ij}=\\cfrac{|(N(i)\\cap N(j))-\\{i,j\\}|}{|(N(i)\\cup N(j))-\\{i,j\\}|}
Oij=∣(N(i)∪N(j))−{i,j}∣∣(N(i)∩N(j))−{i,j}∣
N
(
i
)
N(i)
N(i)表示节点i的邻居集合。
上式中分子是除了ij节点本身外二者的共同邻居,分母是除了ij节点本身外二者所有邻居。
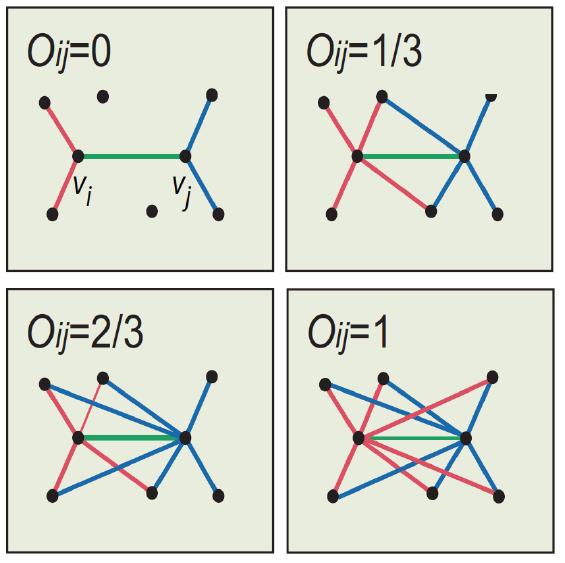
有了这个量化值后,可以看一些实例数据对60年代的理论分析的实证。
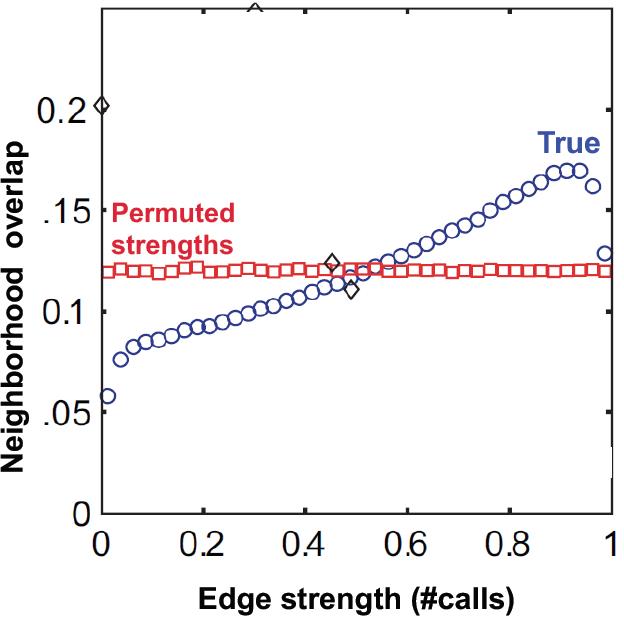
上图中,蓝色是真实的通话数据,红色是保持网络结构不变随机分配通话数量后的结果。
横坐标通话数量和纵坐标edge overlap之间具有正相关性。
将部分数据可视化后(密集community颜色越红):
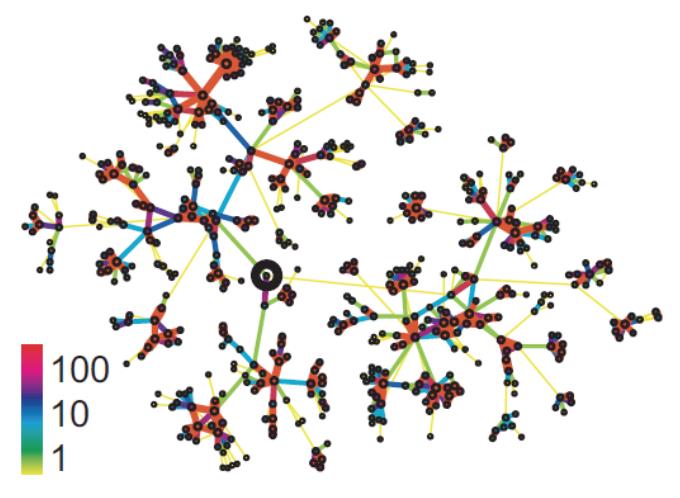
将通信数量随机分配后:
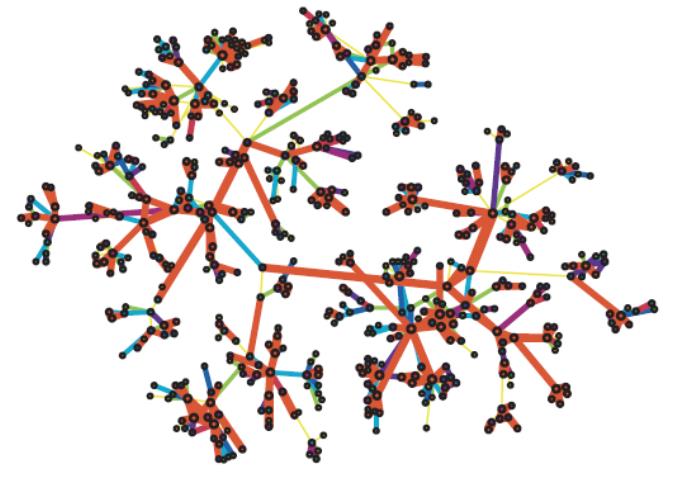
从移边分解实验可以看到
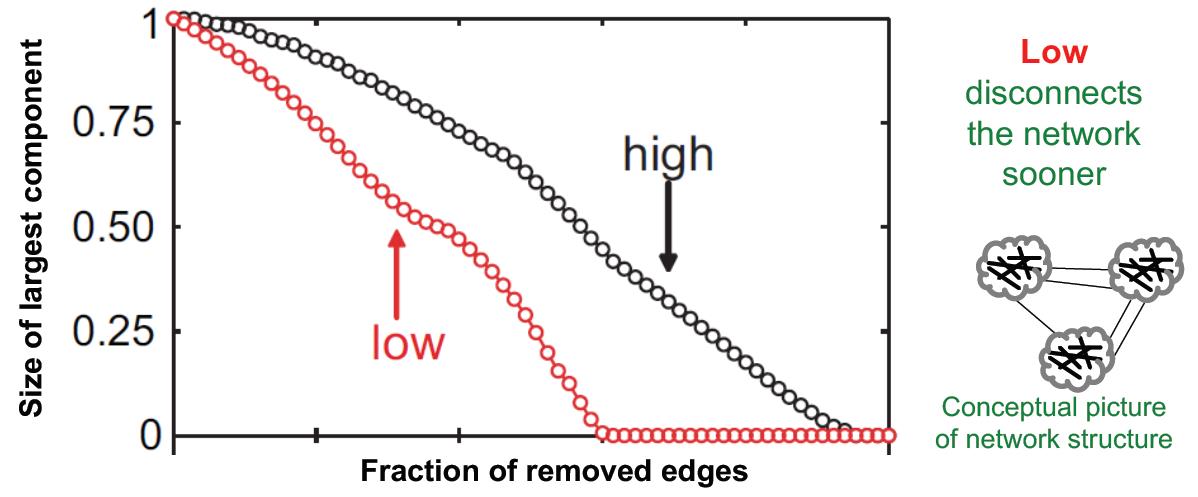
红色是Low to high的overlap移边方式,图分解更快。
黑色是High to low的overlap移边方式,图分解较慢。
Network Communites
下面在看几个从图中找Network Community的例子,然后看如何在图中用数学的方式把Network Community给定义出来。
Network Community的别名还有:clusters, groups, modules
例子
Zachary’s Karate club network
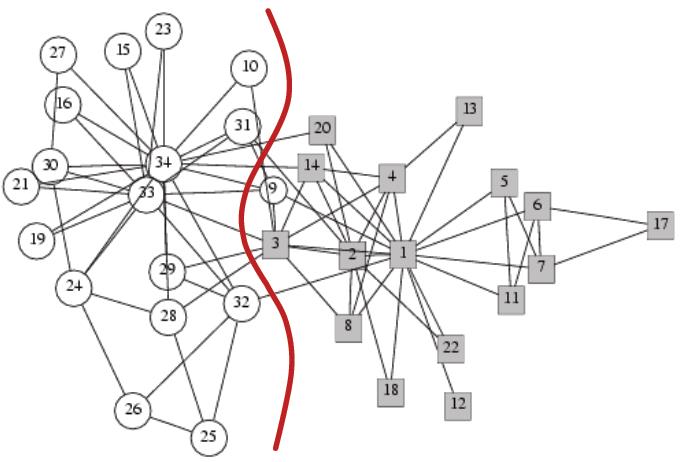
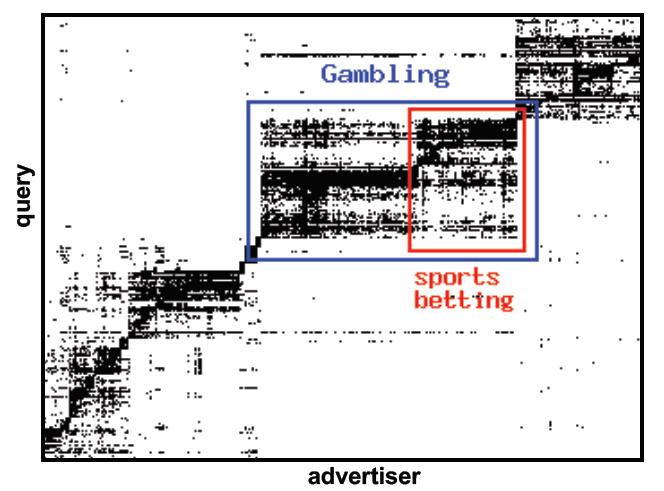
在在线广告投放中,把广告商和查询关键字看做节点,将广告商投放的关键字作为边。可以识别出有针对性的投放区域。
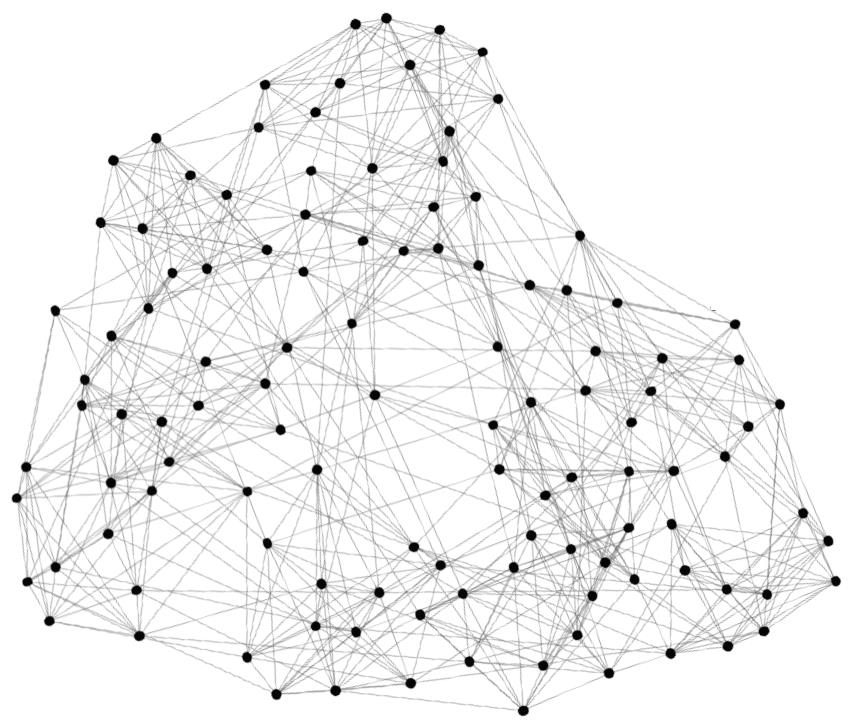
NCAA Football Network,节点是球队,边是球队之间的比赛,原始图这样:
聚类后发现和某些conference(赛区)有关:
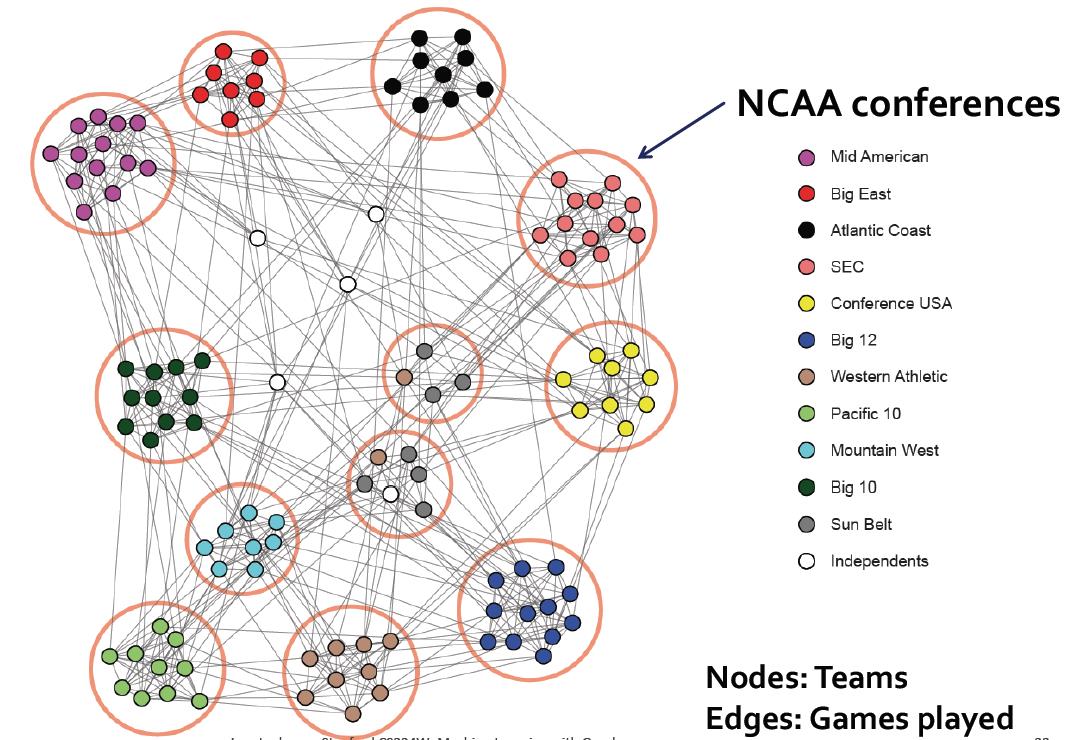
下面看如何找community。
Network Communites的模块化程度
Communities: sets of tightly connected nodes
定义: Modularity 𝑸
A measure of how well a network is partitioned into communities.
Given a partitioning of the network into groups disjoint
s
∈
S
s\\in S
s∈S:
Q
∝
∑
s
∈
S
[
(
# edges within group
s
)
−
(
expeted # edges within group
s
)
]
Q\\propto \\sum_{s\\in S}[(\\text{\\# edges within group }s)-(\\text{expeted \\# edges within group }s)]
Q∝s∈S∑[(# edges within group s)−(expeted # edges within group s)]
这里的后面一项比较难理解,是一个期望,实际上是需要使用随机图(Null Model)来求。
Null Model
给定一个实际的图
G
G
G,该图包含
n
n
n个节点,
m
m
m条边,根据图
G
G
G保持节点和边数量不变(Same degree distribution but uniformly random connections),重新分配边的连接得到图
G
′
G'
G′,而且图
G
′
G'
G′是multigraph,就是允许两个节点间有多条边。
接下来算期望。
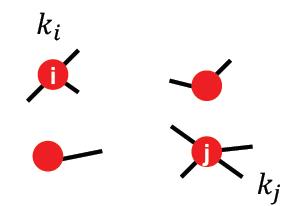
如果把边看成双向的,那么共有
2
m
2m
2m条有向边(这样算是因为节点都象上图一样切开了,每个点的条幅数量加起来就是
2
m
2m
2m),对于出度为
k
i
k_i
ki的
i
i
i节点,其重新连接到节点
j
j
j的概率是:
k
j
2
m
\\cfrac{k_j}{2m}
2mkj,因此重连
i
,
j
i,j
i,j的边的数量期望是:
k
i
⋅
k
j
2
m
=
k
i
k
j
2
m
k_i\\cdot \\cfrac{k_j}{2m}=\\cfrac{k_ik_j}{2m}
ki⋅2mkj=2mkikj
那么计算
G
′
G'
G′的期望总边数为:
G
e
d
g
e
s
_
n
u
m
′
=
1
2
∑
i
∈
N
∑
j
∈
N
k
i
k
j
2
m
=
1
2
⋅
1
2
m
∑
i
∈
N
k
i
(
∑
j
∈
N
k
j
)
=
1
4
m
2
m
⋅
2
m
=
m
G'_{edges\\_num}=\\cfrac{1}{2}\\sum_{i\\in N}\\sum_{j\\in N}\\cfrac{k_ik_j}{2m}=\\cfrac{1}{2}\\cdot\\cfrac{1}{2m}\\sum_{i\\in N}k_i\\left(\\sum_{j\\in N}k_j\\right)=\\cfrac{1}{4m}2m\\cdot2m=m
Gedges_num′=21i∈N∑j∈N∑2mkikj=21⋅2m1i∈N∑ki⎝⎛j∈N∑kj⎠⎞=4m12m⋅2m=m
这里因为条件中讲了,所有节点的边(度)加起来是
2
m
2m
2m,因此:
∑
i
∈
N
k
i
=
∑
i
∈
N
k
j
=
2
m
\\sum_{i\\in N}k_i=\\sum_{i\\in N}k_j=2m
i∈N∑ki=i∈N∑kj=2m
这里也证明了Null Model中与原图的度是一致的。
注意:Null Model可以用在有权图中,有权图可以把权重与度做乘积即可。
Modularity
具体来算Modularity,根据上面的公式: 以上是关于CS224W摘要13.Community Detection in Networks的主要内容,如果未能解决你的问题,请参考以下文章
Q
∝
∑
s
∈
S
[
(
# edges within group
s
)
−
(
expeted # edges within group
s
)
]
Q\\propto \\sum_{s\\in S}[(\\text{\\# edges within group }s)-(\\text{expeted \\# edges within group }s)]
Q∝s∈S∑[(# edges within group s)−(expeted # edges within group s)]
加上具体的数学表达,Modularity公式变成:
Q
(
G
,
S
)
=
1
2
m
∑