智能识别系统设计---图像特征提取

Posted 2021-10-25 NP_hard

文章目录

• 特征提取的简介
• • LBP特征提取
  • • 介绍
    • 原理
    • 代码实现
  • Gabor特征提取
  • • 介绍
    • • Gabor滤波器介绍
      • Gabor特征介绍
    • 原理
    • 代码实现
    • • 生成一个Gabor滤波器并对图像进行滤波
      • Gabor特征提取
  • 基于颜色直方图的特征提取与反向投影
  • • 介绍
    • 代码
    • • 图片的RGB像素分布和HSV像素分布图
• 末尾

特征提取的简介

特征提取：通过统计或学习等方法从图像中提取出能够有效表示原始图像内容的特征向量的集合

LBP特征提取

这位大哥讲的很不错

介绍

局部二值模式（Local Binary Patter,LBP）是一种用来描述图像局部纹理特征的算子
由于计算简单，可用于基于纹理分类的实时应用场景，例如目标检测，人脸识别（LBP+AdaBoost）

LBP特征只考虑纹理信息，不包含颜色信息，因此彩色图需转换为灰度图

原理

LBP特征提取操作可以去除光照对图片的影响

对于一张单通道灰度图，我们对每一个像素进行如下操作：

首先，我们可以取这个像素点X以及其周围一圈8个像素点，组成3x3的像素矩阵（每个像素的灰度值的范围 0-255）

对于这个3x3的矩阵，对其进行LBP操作，将其二值化

公式：
$$LBP(x_c,y_c)=\sum _{p=0}^{p-1}{2}^{p}s(i_p-i_c)$$$$s(x)=\{\begin{array}{ll}1& ifx\ge 0\\ 0& else\end{array}$$
二值化后的矩阵

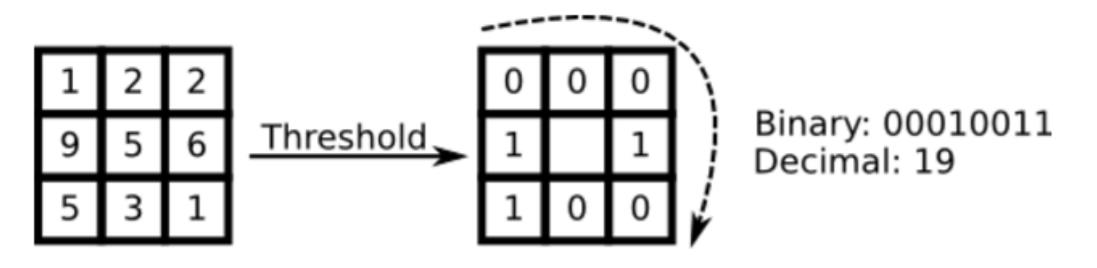
然后将像素点X外的一圈01值重组为一个长度为9的二进制数，这个二进制数对应的十进制数即为像素点X的新值

代码实现

导入算法所需的包

import cv2  as cv
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm

读入所需处理的单通道灰度图

filepath='anime2.PNG'
img=cv.imread(filepath,0)
plt.imshow(img,cmap='gray')
print("img shape:",img.shape)

img shape: (654, 843)

这是自己实现的LBP函数

def LBP(img):
    dst=np.zeros(img.shape,dtype=img.dtype)
    for i in range(1,img.shape[0]-1):
        for j in range(1,img.shape[1]-1):
            center=img[i][j]
            code=0
            code |= (img[i-1][j-1]>=center)<<7
            code |= (img[i-1][j  ]>=center)<<6
            code |= (img[i-1][j+1]>=center)<<5
            code |= (img[i  ][j+1]>=center)<<4
            code |= (img[i+1][j+1]>=center)<<3
            code |= (img[i+1][j  ]>=center)<<2
            code |= (img[i+1][j-1]>=center)<<1
            code |= (img[i  ][j-1]>=center)<<0

            dst[i][j]=code
    return dst

进行LBP处理

plt.imshow(LBP(img),cmap='gray')

再测试一下，是否对阳光干扰有作用

img_=cv.imread('beam_face.jpg',0)

plt.figure(figsize=[8,8])
plt.subplot(2,2,1)
plt.imshow(cv.cvtColor(img_,cv.COLOR_BGR2RGB))
plt.title('src image')

plt.subplot(2,2,2)
plt.imshow(cv.cvtColor(LBP(img_),cv.COLOR_BGR2RGB))
plt.title('LBP image')

貌似有用?

Gabor特征提取

介绍

Gabor滤波器介绍

实在看不懂，转载一位大哥的博客内容

在图像处理中，Gabor函数是一个用于边缘提取的线性滤波器，Gabor函数十分适合纹理表达和分离。

在空间域中，一个二维Gabor滤波器是一个由正弦平面波调制的高斯核函数。

Gabor滤波器的脉冲响应，可以定义为一个正弦波（对于二维Gabor滤波器是正弦平面波）乘以高斯函数。由于乘法的卷积性质，Gabor滤波器的脉冲响应的傅立叶变换是其调和函数的傅立叶变换和高斯函数傅立叶变换的卷积。该滤波器由实部和虚部组成，二者相互正交。

一组不同频率不同方向的Gabor函数对于图像特征提取非常有用。

Gabor特征介绍

Gabor函数可以在频域上不同尺度，不同方向上提取相关的特征（采用不同参数的Gabor函数），由于Gabor函数与人眼的作用相仿，所以常用在纹理识别上。

Gabor特征提取主要包含取模，特征降维，特征归一化和特征选取等操作。

• 取模
  就是使用图像变换后的实部和虚部的模（二范数）作为图像特征.
  $$mod(combine)=\sqrt{rea{l}^2+ima{g}^2}$$
• 特征降维
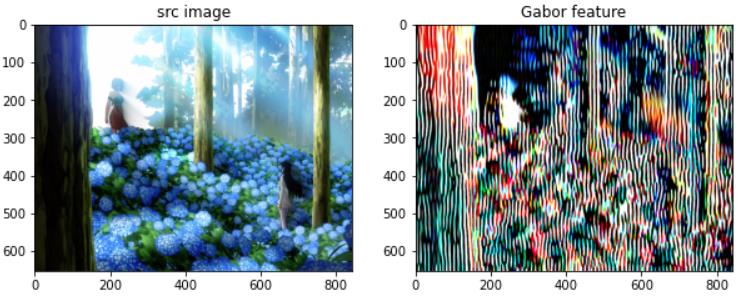
  图像识别领域一般使用8个方向和5个尺度的Gabor滤波器，会得到40幅变换图像，这些变换图像的特征串联起来即为图像的特征（40维的特征），由于特征维度较高，故需要降维。最简单的方法就是对每个模图像进行下采样。

下图为图像的一个变换图像（即使用了一个Gabor滤波器对原图像滤波后得到的图像）

• 特征归一化
  一般使用Z-score标准化方法
  $$x=\frac{x-\mu }{\sigma }$$
  • 本方法要求原始数据的分布为高斯分布，不然归一化的效果很糟糕。
  • 在分类，聚类算法中，需要使用距离来度量相似性的时候，或者使用PCA技术进行降维的时候，Z-score 标准化方法表现更好
• 特征选取
  在经过以上三步之后，图像特征（各模图像串联得到）可能存在大量冗余，最好在进行一次特征选择操作，可以使用PCA或Fisher等线性子空间分析方法

原理

通过Gabor函数生成Gabor滤波器（size x size的矩阵），再利用Gabor滤波器对图像进行卷积（滤波）操作，得到包含Gabor特征的图像

Gabor函数：$$g^{\varphi }(x,y)=g(x,y,{\sigma }_x,{\sigma }_y,f_x,f_y,\theta )$$ $$=exp(-((\frac{X(x,y,\theta )}{{\sigma }_x})+(\frac{Y(x,y,\theta )}{{\sigma }_y})))exp(i(f_{x}x+f_{y}y))$$
其中：$$X(x,y,\theta )=xcos(\theta )+ysin(\theta )$$$$Y(x,y,\theta )=-xsin(\theta )+ycos(\theta )$$

• x和y为坐标，θ是Gabor的方向
• ${\sigma }_x$和${\sigma }_y$分别是x和y方向的带宽，是一个标量参数
• $f_x$和$f_y$分别是x和y方向的中心调频，是一个标量参数

实部：
g e ϕ ( x , y ) = e x p ( − ( ( X σ x ) 2 + ( Y σ y ) 2 ) ) c o s ( f x x + f y y ) g_e^\\phi(x,y)=exp(-((\\frac{X}{σ_x})^2+(\\frac{Y}{σ_y})^2))cos(f_xx+f_yy) geϕ​(x,y)=exp(−((σx​X​)以上是关于智能识别系统设计---图像特征提取的主要内容，如果未能解决你的问题，请参考以下文章

人脸识别系统技术方案

求人脸识别源代码

人工智能_1_初识_机器学习介绍_特征工程和文本特征提取

智能门锁人脸识别技术的原理是怎样的？

毕设题目：Matlab车牌识别

毕设题目：Matlab指纹识别