4.Spark ML学习笔记—Spark ML决策树 (应用案例)随机森林GBDT算法ML 树模型参数详解 (本篇概念多)

Posted 2021-10-25 页川叶川

本文目录如下：

• 第4章 Spark ML决策树、随机森林、GBDT算法
• • 4.1 Spark ML决策树
  • • 4.1.1 决策树定义
    • 4.1.2 决策树学习过程
    • 4.1.3 特征选择
    • • 4.1.3.1 特征选择: 熵
      • 4.1.3.2 特征选择: 基尼
      • 4.1.3.3 特征选择: 方差
    • 4.1.4 生成决策树的方法: ID3算法
    • 4.1.5 使用决策树算法建立一个可扩展的分类器
  • 4.2 集成学习
  • • 4.2.1 Bagging 方法
    • 4.2.2 Boosting 方法
    • 4.2.3 Bagging 方法 和 Boosting 方法 的区别
  • 4.3 随机森林
  • • 4.4 GBDT
  • 4.5 ML 树模型参数详解
  • • 4.5.1 DecisionTreeClassifier
    • 4.5.2 RandomForestRegressor
    • 4.5.3 GBTClassifier

第4章 Spark ML决策树、随机森林、GBDT算法

4.1 Spark ML决策树

4.1.1 决策树定义

• 决策树(decision tree) 通常被认为适用于解决 分类 和 回归 任务的监督学习技术。
• 决策树 是一个树结构，决策树由 节点 和 有向边 组成。
• 节点有两种类型: 内部节点 和 叶节点，内部节点表示一个 特征 或 属性，叶节点表示一个类。
• 其每个 非叶节点 表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出。

4.1.2 决策树学习过程

• 决策树学习的本质是从训练数据集上归纳出一组分类规则，通常采用启发式的方法: 局部最优。
• 具体做法就是，每次选择 feature 时，都挑选当前条件下最优的那个 feature 作为 划分规则，即局部最优的 feature。
• 决策树学习通常分为3个步骤: 特征选择、决策树生成 和 决策树的修剪。
  

4.1.3 特征选择

选择特征的标准是找出局部最优的特征， 判断一个特征对于当前数据集的分类效果。也就是按照这个特征进行分类后，数据集是否更加有序 (不同分类的数据被尽量分开)。

衡量节点数据集合的有序性 (纯度) 有:

• 嫡 (分类)
• 基尼 (分类)
• 方差 (回归)

4.1.3.1 特征选择: 熵

• (1) 信息量
  信息量 由这个事件发生的 概率 所决定。经常发生的事件是没有什么信息量的，只有小概率事件才有信息量，(一个事件发生的越频繁, 信息量越小)。所以信息量的定义:
  
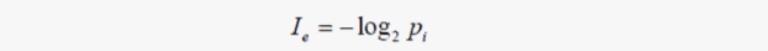
• (2) 信息熵
  嫡，就是信息量的期望，信息嫡的公式为:
  
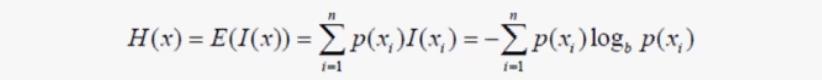
  条件熵的公式为:
  
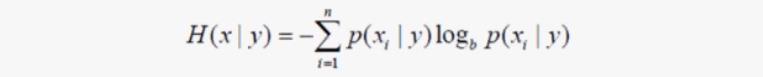
• (3) 信息增益

分类前，数据中可能出现各种类的情况，比较混乱，不确定性强，熵比较高; 分类后 不同类的数据得到比较好的划分，那么在一个划分中大部分是同一类的数据，比较有序，不确定性降低，熵比较低。信息增益就是用于这种嫡的变化。

信息增益 的定义为: 特征 A 对训练数据集 D 的信息增益 g(D, A)，定义为集合 D 的经验嫡 H(D) 与特征 A 给定条件下 D 的经验条件嫡 H(D|A) 之差，即:

其中, H(D) 根据信息嫡的公式计算得到。

而 H(D|A)，D 根据 A 分为 n 份 D1...Dn，那么 H(DlA) 就是所有 H(Di) 的期望 (平均值)

• (4) 信息增益比

单纯的信息增益只是个相对值，因为这依赖于 H(D) 的大小，所以信息增益比更能客观地反映信息增益。

信息增益比的定义为: 特征 A 对训练数据集 D 的信息增益比 gR(D|A) 定义为其信息增益 g(D,A) 与分裂信息嫡split_info(A)之比:

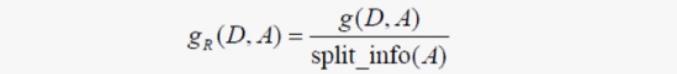
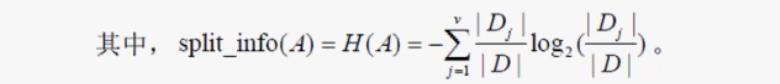
4.1.3.2 特征选择: 基尼

• 基尼指数是另一种数据的不纯度的度量方法，其公式为:
  

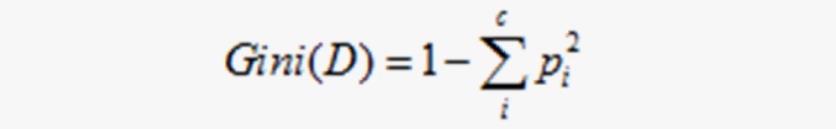
• 其中 c 表示数据集中 类别的数量，Pi 表示类别 i 样本数量占所有样本的比例。

• 从该公式可以看出，当数据集中数据混合的程度越高，基尼指数也就越高。当数据集 D 只有一种数据类型，那么基尼指数的值为最低 0。

• 例: 有 10 个类别，每个类别出现的概率平均为 0.1，则 pi平方 = 0.01，所有类别的 pi平方 之和为 0.1，则基尼为 0.9，数值较大，表示混合度较高。

4.1.3.3 特征选择: 方差

方差公式是一个数学公式，用来度量 随机变量 和其 数学期望 (即均值)之间的偏离程度，方差越小，代表这组数据越稳定，方差越大，代表这组数据越不稳定。

4.1.4 生成决策树的方法: ID3算法

• ID3算法 就是在每次需要分裂时，计算每个属性的增益率，然后选择增益率最大的属性进行分裂。
• 算法过程: 略…

4.1.5 使用决策树算法建立一个可扩展的分类器

• (1) 创建数据帧

var data = spark.read.format("libsvm").load("datas3/Letterdata_libsvm.data")

• (2) 标签索引

val labelIndexer = new StringIndexer()
  .setInputCol("label")
  .setOutputCol("indexedLabel")
  .fit(data)

• (3) 识别分类特征

val featureIndexer = new VectorIndexer()
  .setInputCol("features")
  .setOutputCol("indexedFeatures")
  .setMaxCategories(4)
  .fit(data)

• (4) 准备训练和测试集

val Array(trainingData, testData) = data.randomSplit(Array(0.75, 0.25), 1234L)

• (5) 训练 DT 模型

val dt = new DecisionTreeClassifier()
  .setLabelCol("indexedLabel")
  .setFeaturesCol("indexedFeatures")

• (6) 将索引后的标签换回原始标签

val labelConverter = new IndexToString()
  .setInputCol("prediction")
  .setOutputCol("predictedLabel")
  .setLabels(labelIndexer.labels)

• (7) 创建 DT pipeline

val pipeline = new Pipeline().setStages(Array(labelIndexer, featureIndexer, dt, labelConverter))

• (8) 运行索引生成器使用转换器

val model = pipeline.fit(trainingData)

• (9) 在测试集上计算预测

val predictions = model.transform(testData)
predictions.show()

• (10) 评估模型、计算性能度量指标、打印性能度量指标
  略…

• (11) 打印 DT 结点

val treeModel = model.stages(2).asInstanceOf[DecisionTreeClassificationModel]
println("Learned classification tree model: \\n" + treeModel.toDebugString)

---

4.2 集成学习

集成学习(Ensemble learning )是一种机器学习范式，它使用多个 弱分类器 来解决同一个问题，可以提高 分类 和 回归 的准确性。而最具代表性的就是 Bagging 和 Boosting 方法。

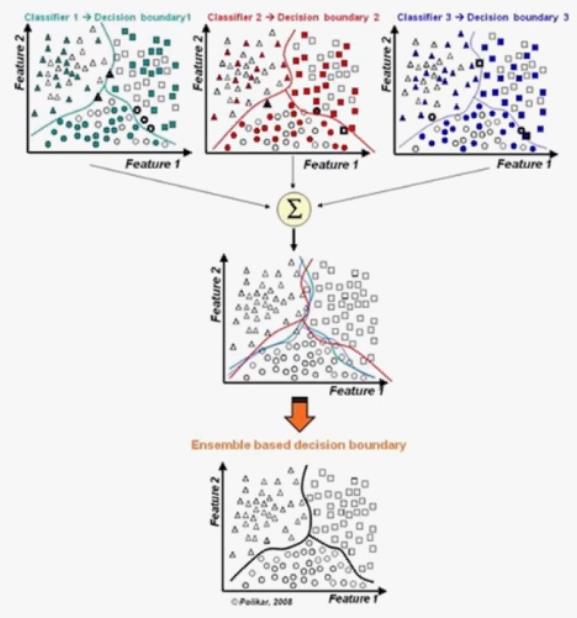
4.2.1 Bagging 方法

有放回抽样得到 S 个样本集，用同一个分类算法分别作用于每个样本集得到 S 个分类器，选择分类器投票结果最多的类别作为分类结果，代表有随机森林。

4.2.2 Boosting 方法

基于 错误，不断 迭代修正 提升分类器性能。代表有 Adaboost (Adaptive boosting ) 和GBDT (Gradient Boosting Decision Tree)

4.2.3 Bagging 方法 和 Boosting 方法 的区别

• Bagging 中不同分类器是 并行 得到的，而 Boosting 中每个分类器通过 串行 训练得到(关注被已有分类器错分的样本获得新分类器)
• Bagging 中各个分类器权重相同，Boost 则是不同的（Boosting 分类的结果基于所有分类器的加权求和结果的)

---

4.3 随机森林

将样本集分成 n 个子集， 每个子集训练成为一个 决策树, 则并行的到了 n 个分类器，然后再把 n 个 决策树 进行合并, 求平均值，最终得到一个预测结果。

---

4.4 GBDT

• 决策树是在一棵树上进行学习, 而 GBDT 是基于前面n棵树的残差进行学习。
• 每一棵树是基于前面n棵树的残差进行学习，使得尽可能的整体残差最小，所以每增加一棵树，就是在这个残差优化走一小步，最终找到最优值。
  

基于残差的 Boosting:

---

4.5 ML 树模型参数详解

4.5.1 DecisionTreeClassifier

4.5.2 RandomForestRegressor

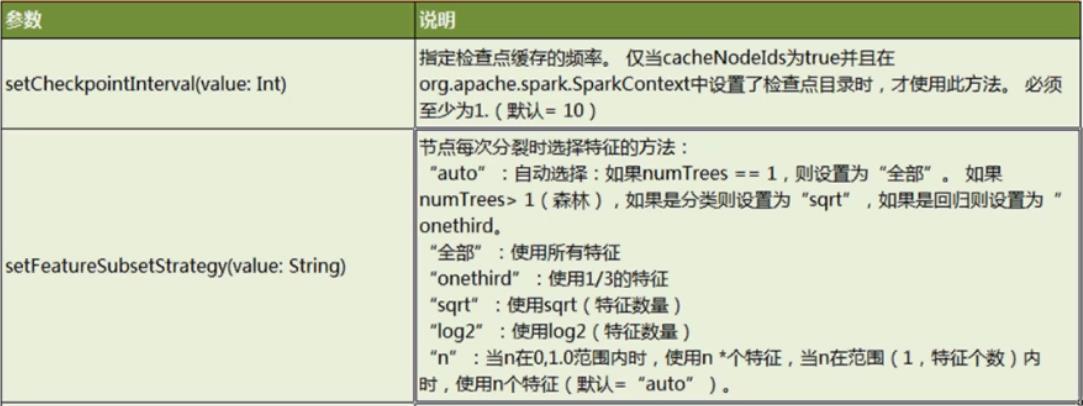
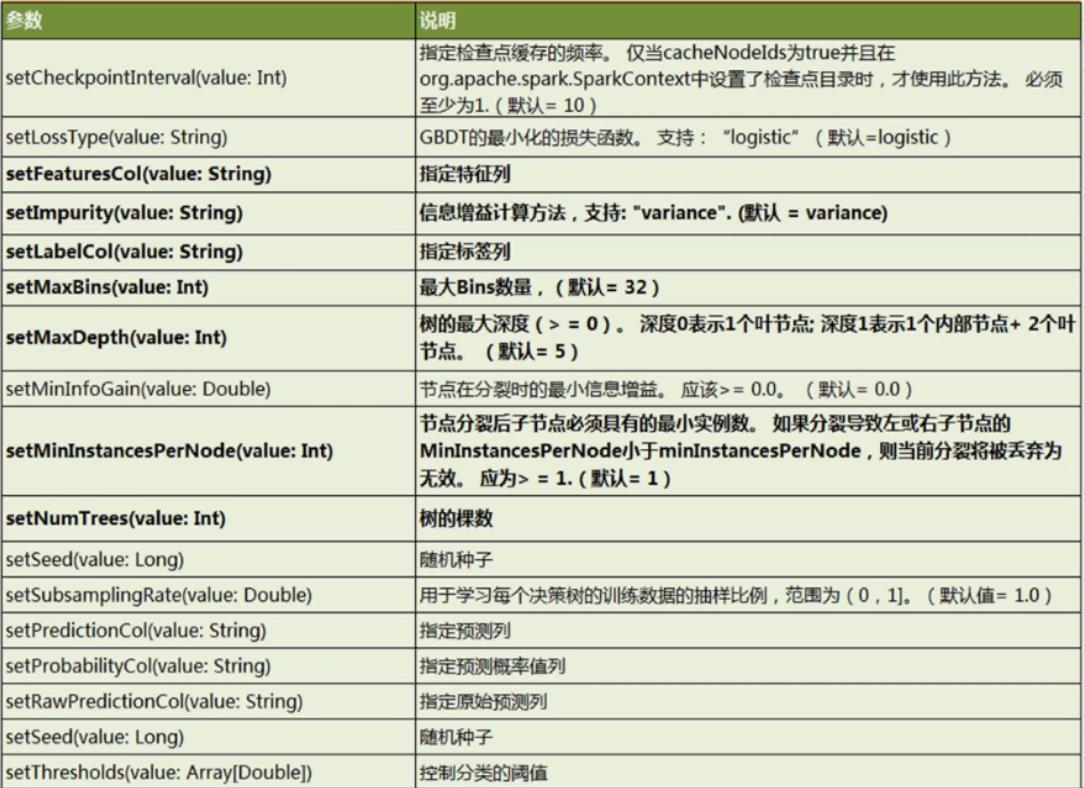
4.5.3 GBTClassifier