第2章 关系2
Posted 可能自洽
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第2章 关系2相关的知识,希望对你有一定的参考价值。
第2章 关系2
五、关系上的闭包运算
1.关系闭包的概念
1.1 定义 设R是X上的关系,则R的自反(对称、传递)闭包是同时满足下面3个条件的一个新关系 R ′ R' R′
1) R是自反的(对称的、传递的)
2) R ⊆ R ′ R \\subseteq R' R⊆R′
3) 如果X上的关系 R ′ ′ R'' R′′是自反的(对称的、传递的),且 R ⊆ R ′ ′ R \\subseteq R'' R⊆R′′,则有 R ′ ⊆ R ′ ′ R' \\subseteq R'' R′⊆R′′
R的自反闭包是包含R、具有自反性、元素最少的关系
可以证明: R的自反闭包是包含R的具有自反性质的所有关系的交
1.2 设R是X上的关系.由定义,下面结论是显然或容易证明的
1) 三种关系的闭包都是唯一的,今后分别用 r ( R ) , s ( R ) 和 t ( R ) r(R),s(R)和t(R) r(R),s(R)和t(R)表示关系R的自反闭包、对称闭包和传递闭包.显然,求一个关系自反闭包、对称闭包、传递闭包的过程是关系的一元运算
2) r ( R ) , s ( R ) 和 t ( R ) r(R), s(R)和t(R) r(R),s(R)和t(R)分别是自反的、对称的和传递的关系
3) r ( R ) , s ( R ) 和 t ( R ) r(R),s(R)和t(R) r(R),s(R)和t(R)分别是包含R的自反关系、对称关系和传递关系中最小的关系(定义三个条件,其中最小性由条件 3) 保证)
4) 即自反、对称和传递关系的闭包是它们自身
R
是
自
反
的
⇔
r
(
R
)
=
R
R是自反的 \\Leftrightarrow r(R)=R
R是自反的⇔r(R)=R
R
是
对
称
的
⇔
s
(
R
)
=
R
R是对称的 \\Leftrightarrow s(R)=R
R是对称的⇔s(R)=R
R
是
传
递
的
⇔
t
(
R
)
=
R
R是传递的 \\Leftrightarrow t(R)=R
R是传递的⇔t(R)=R
2.关系闭包的计算公式
2.1 设R是X上的关系,则
r
(
R
)
=
R
∪
I
X
r(R)=R \\cup I_{X}
r(R)=R∪IX
s
(
R
)
=
R
∪
R
~
s(R)=R \\cup \\tilde{R}
s(R)=R∪R~
t
(
R
)
=
⋃
i
=
1
∞
R
i
t(R)=\\bigcup_{i=1}^{\\infty} R^{i}
t(R)=⋃i=1∞Ri
2.2 设R是n元集合X上的关系,则 t ( R ) = ⋃ i = 1 n R i t(R)=\\bigcup_{i=1}^{n} R^{i} t(R)=⋃i=1nRi
例 设字母表 V = { A , B , C , D , e , d , f } V=\\{A,B,C,D,e,d,f\\} V={A,B,C,D,e,d,f},有六条语法规则 A → A f , A → B , B → D d e , B → D e , C → e , D → B f A \\rightarrow Af,A \\rightarrow B,B \\rightarrow Dde,B \\rightarrow De,C \\rightarrow e,D \\rightarrow Bf A→Af,A→B,B→Dde,B→De,C→e,D→Bf,在V上定义关系R如下 R = { ( x , y ) ∣ x , y ∈ V , 从 x 出 发 仅 使 用 一 条 规 则 能 推 出 的 字 符 串 的 首 字 符 为 y } R= \\{(x,y)|x, y∈V,从x出发仅使用一条规则能推出的字符串的首字符为y\\} R={(x,y)∣x,y∈V,从x出发仅使用一条规则能推出的字符串的首字符为y}
首先,由R的定义得
R
=
{
(
A
,
A
)
,
(
A
,
B
)
,
(
B
,
D
)
,
(
D
,
B
)
,
(
C
,
e
)
}
R = \\{(A,A),(A, B),(B, D),(D, B),(C,e)\\}
R={(A,A),(A,B),(B,D),(D,B),(C,e)}
t
(
R
)
=
{
(
A
,
A
)
,
(
A
,
B
)
,
(
B
,
D
)
,
(
D
,
B
)
,
(
C
,
e
)
,
(
B
,
B
)
,
(
A
,
D
)
,
(
D
,
D
)
}
t(R)=\\{(A,A),(A,B),(B, D),(D, B),(C,e),(B, B),(A, D),(D,D)\\}
t(R)={(A,A),(A,B),(B,D),(D,B),(C,e),(B,B),(A,D),(D,D)}
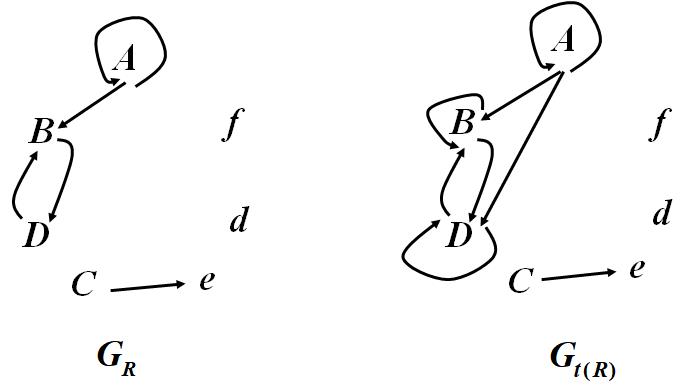
从A出发连续使用语法规则推出字符串首字符为:A,B,D
从B出发连续使用语法规则推出字符串首字符为:B, D
从D出发连续使用语法规则推出字符串首字符为:B,D
从C出发连续使用语法规则推出字符串首字符为:e
形式语言中大写字母称为非终结符,小写字母称为终结符,规则称为产生式
六、次序关系
1.偏序关系定义
设R是集合X上的关系。如果R是自反、反对称和传递的,则称R是X上的偏序关系,且称X是R的偏序集,今后经常用符号“≤”来表示偏序关系.
集合X上的恒等关系是X上“ 最小”的偏序关系
例 定义三个关系如下
⊆
=
{
(
x
,
y
)
:
x
,
y
∈
2
A
,
x
是
y
的
子
集
}
\\subseteq=\\{(x, y): x, y \\in 2^{A}, x是 y 的子集 \\}
⊆={(x,y):x,y∈2A,x是y的子集}, 其中 A 是任意集合
∣
=
{
(
x
,
y
)
:
x
,
y
∈
D
,
x
整
除
y
}
\\mid=\\{(x, y): x, y \\in D, x 整除 y\\}
∣={(x,y):x,y∈D,x整除y} , 其中 D 是任意正整数集合
≤
=
{
(
a
,
b
)
:
a
,
b
∈
B
,
a
小
于
或
等
于
b
}
\\leq=\\{(a, b): a, b \\in B, a小于或等于 b\\}
≤={(a,b):a,b∈B,a小于或等于b} , 其中 B 是任意实数集
利用偏序关系的定义可以证明
⊆
\\subseteq
⊆是集合A的幂集
2
A
2^{A}
2A上的偏序关系
∣
\\mid
∣是任意正整数集合D上的偏序关系
≤
\\leq
≤是任意实数集合B上的偏序关系
2.拟序关系定义
设R是X上的关系,如果R是反自反并且传递的,则称R是X上的拟序关系,今后常用符号“<”表示拟序关系。
空关系是拟序,拟序关系的逆和交仍是拟序关系,但拟序关系的并、复合等一般不再是拟序关系
例 定义两个关系如下
⊂
=
{
(
x
,
y
)
:
x
,
y
∈
2
A
,
x
是
y
的
真
子
集
}
\\subset=\\{(x, y): x, y \\in 2^{A}, x是 y 的真子集 \\}
⊂={(x,y):x,y∈2A,x是y的真子集} , 其中 A 是任意集合
<
=
{
(
a
,
b
)
:
a
,
b
∈
B
,
a
小
于
b
}
<=\\{(a, b): a, b \\in B, a 小 于 b\\}
<={(a,b):a,b∈B,a小于b}, 其中 B 是任意实数集
则
⊂
\\subset
⊂是
2
A
2^{A}
2A上的拟序关系;
<是B上的拟序关系
2.1 集合X上的拟序关系R一定是反对称的
证明:
假设R不是反对称的,则存在元素x≠y∈X,使得xRy且yRx.由于R是拟序,于是它是传递的,从而xRx,这与R是反自反的矛盾.
3.集合X上的偏序和拟序关系
3.1 共同点和不同点
共同点:它们都是反对称和传递的,
不同点:偏序是自反的,而拟序是反自反的.
因此,得到
偏序可看成是拟序+自反,即拟序的条件扩充
拟序可看成是偏序-自反,即偏序的条件缩减
3.2 定理:设R是X上的关系
1)若R是拟序关系,则 R ∪ I X = r ( R ) R \\cup I_{X} =r(R) R∪