CS224W摘要12.Frequent Subgraph Mining with GNNs

Posted 2021-10-23 oldmao_2000

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了CS224W摘要12.Frequent Subgraph Mining with GNNs相关的知识，希望对你有一定的参考价值。

文章目录

Subgraph and Motifs
Neural Subgraph Matching / Representations
Mining / Finding Frequent Motifs / Subgraphs

CS224W: Machine Learning with Graphs
公式输入请参考：在线Latex公式
本节课三部分内容
子图的概念和定义，其重要性指标。
子图的表征，如果用GNN的方式进行子图的表征
子图频率的挖掘

Subgraph and Motifs

先要明确子图的概念，就好比乐高中的模块一样，不能切分太小，又不能切分太多，如何识别出图中的子图模块。

Definitionn of Subgraphs

有两种。Given graph 𝑮 = (𝑽, 𝑬)
选择的方式主要看应用，例如：
Chemistry: node-induced (functional groups)
Knowledge graphs: Often edge-induced (focus is on edges representing logical relations)

Node-induced subgraph

Take subset of the nodes and all edges induced by the nodes:
$G^{'} = (V^{'}, E^{'})$ is a node induced subgraph iff
$𝑉'\\nsubseteq V$
$𝐸′ = \\{(𝑢, 𝑣) ∈ 𝐸 | 𝑢, 𝑣 ∈ 𝑉'\\}$
$G^{'}$ is the subgraph of 𝐺 induced by $V^{'}$
也叫：induced subgraph由节点集决定的子图

Edge-induced subgraph

Take subset of the edges and all corresponding nodes
$G^{'} = (V^{'}, E^{'})$ is an edge induced subgraph iff
$E^{'} \subseteq E$
$𝑉'=\\{𝑣∈𝑉|(𝑣,𝑢)∈𝐸′\\text{ for some }𝑢\\}$
也叫：“non-induced subgraph” or just “subgraph”，较少用

contained subgraph

上面两种子图定义都是针对从源图中取的子图，如果节点或者边是来自不同的图：

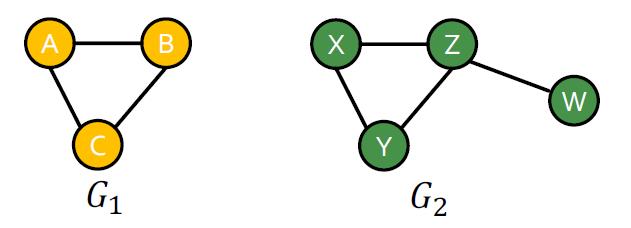
那么我们把两个图称为包含关系。确定包含关系的关键之处就是确定图是否同构。

Graph isomorphism

由于节点的无序性，同构可能是NP-hard的问题（未证明），具体定义如下：
如果两个图存在一个双射函数（bijection function） $f$ ，使得：
$(u,v)\\in E_1 \\text{ iff }(f(a),f(b))\\in E_2$
$f$ 就是同构关系。

子图的同构问题与上面的包含关系等价。这个是NP-hard的问题

$G_2$ is subgraph-isomorphic to $G_1$ if some subgraph of $G_2$ is isomorphic to $G_1$ .

可以看到函数 $f$ 不是唯一的的，这里的点顺序可以换一下，不影响结果。

然后给出不同节点数量（大小）的非同构的子图例子（3个节点有向）：

4个节点无向：

Determining Motif Significance

有了上面的结论，可以继续往下推，就是一个图结构可以分解为上面的一个个小的子图构成，构成图结构的一个个小的子图就是Motif

Network motifs

概念：recurring, significant patterns of interconnections
实际生活中的例子就是（图片来自百度）：

因此得到motif的三个特征：
Pattern: Small (node-induced) subgraph
Recurring: Found many times, i.e., with high frequency
Significant: More frequent than expected, i.e., in randomly generated graphs?

一个motif匹配的例子（induced表示是基于节点的）：

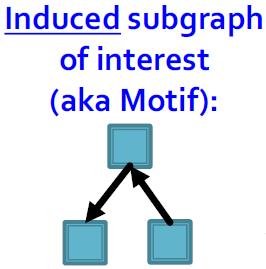
Motifs的作用

Help us understand how graphs work.了解图的工作机制
Help us make predictions based on presence or lack of presence in a graph dataset.做主题预测，某个主题往往包含特定的motif，例如社交网络中往往是三角形的motif
例子：
Feed-forward loops: found in networks of neurons, where they neutralize “biological noise”

Parallel loops: found in food webs（食物链？）

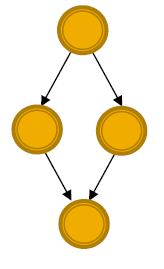
Single-input modules: found in gene control networks

subgraph frequency

$G_Q$ 是小图， $v$ 是小图中的某个锚点， $G_T$ 是目标图
Graph-level Subgraph Frequency Definition.
找出 $G_Q$ 在 $G_T$ 中出现的频率：number of unique subsets of nodes $V_T$ of $G_T$ for which the subgraph of $G_T$ induced by the nodes $V_T$ is isomorphic to $G_Q$
例子：

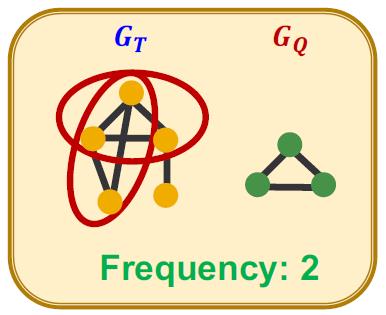
Node-level Subgraph Frequency Definition:
The number of nodes $u$ in $G_T$ for which some subgraph of $G_T$ is isomorphic to $G_Q$ and the isomorphism maps $u$ to $v$ .
记 $C_Q,v)$ 为node-anchored subgraph。这种方法对outlier的鲁棒性较好。
例如：

可以看到中心点只算了一次。
如果 $G_T$ 是多个图，则可以将不同的图看成同一个图的非连通子图进行计算。