一文通数据结构与算法之——回溯算法+常见题型与解题策略+Leetcode经典题

Posted 尚墨1111

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了一文通数据结构与算法之——回溯算法+常见题型与解题策略+Leetcode经典题相关的知识，希望对你有一定的参考价值。

文章目录

回溯算法

1 基本内容

1.1 回溯算法的框架

解决一个回溯问题，实际上就是一个决策树的遍历过程。你只需要思考 3 个问题：

1、路径：也就是已经做出的选择。

2、选择列表：也就是你当前可以做的选择。

3、结束条件：也就是到达决策树底层，无法再做选择的条件。

result = []
public List<Integer> backtrack(路径, 选择列表){
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择
}

1.2 回溯核心思想

1、每一次的backtrack，是在回溯深度，如二叉树的深度遍历，所以我们要知道深度在这道题中的意义

  • 比如对于N皇后问题，深度就是二维数组的行，所以每一次是backtrack(row+1)
  • 比如分割字符串问题，深度就是字符串的长度，所以每一次是backtrack(start+1)
  • 比如全排列问题，深度就是字符串的长度，所以每一次是backtrack(i+1)
back(s,start+i,path);
trackBack(nums,target-nums[i],i,path);

2、在每一个backTrace中的for循环代表什么意思，就是在当前状态下你的所有选择

  • 比如恢复IP中，你的选择是 用1还是2 还是 3作为这一段的长度
  • 对于N皇后问题，你的选择就是这一层的那一个列的位置 col作为皇后的位置
for (int i = start; i < num.length ; i++) {//长度的选择
    ...
}
for (int i = 1; i <=3 ; i++) {//切分的选择
    ...
}

3、剪枝

  • 不像动态规划存在重叠子问题可以优化，回溯算法就是纯暴力穷举，复杂度一般都很高。

  • 把没有必要的枝叶剪去的操作就是剪枝，在代码中一般通过 break 或者 contine 和 return （表示递归终止）实现。

if(i>0 && nums[i]==nums[i-1] && !isVisit[i-1]){
    continue;
}
if(list.contains(num[i])){
    continue;
}
if(i==3 && temp.compareTo("255")>0){
    return ;
}

1.3 回溯法解决的问题

回溯法，一般可以解决如下几种问题：

  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 分割问题：一个字符串按一定规则有几种切割方式
  • 棋盘问题：N皇后，解数独

注意组合和排列的区别：

组合是不强调元素顺序的，排列是强调元素顺序。

{1, 2} 和 {2, 1} 在组合上，就是同一个，而要是排列的话，{1, 2} 和 {2, 1} 就是两个排列

1.4 题目列表

全排列

子集

组合

分割

棋盘

1.4 常见问题分析

明明设置了起始位置，但是结果中还是加入了起始位置前的元素——回溯起始位置问题的是i但是填成了start

输入：nums = [1,2,3]
输出：[[],[1],[1,2],[1,2,3],[1,3],[2],[2,3],[3],[3,2]]//[3,2]这种情况

输出的集合中的元素，远超过限制的元素，忘记在回溯的时候撤销选择了

path.removeLast()

输出的组合比答案少——是否剪枝的时候没有排序？

if(target-nums[i]<0){
    break;
}

输出下面这种情况，是因为char[] 没有初始化

[[".Q\\u0000\\u0000","\\u0000\\u0000.Q","Q.\\u0000\\u0000",
"\\u0000\\u0000Q\\u0000"],["..Q\\u0000","Q\\u0000..",
"..\\u0000Q","\\u0000Q.\\u0000"]]

String知识

//String.compareTo()方法
//如果第一个字符和参数的第一个字符不等，结束比较，返回第一个字符的ASCII码差值。
//如果第一个字符和参数的第一个字符相等，则以第二个字符和参数的第二个字符做比较，以此类推,直至不等为止，返回该字符的ASCII码差值。 //如果两个字符串不一样长，可对应字符又完全一样，则返回两个字符串的长度差值。
	@Test
    public void test(){
        //输出 5，第一个字符相同，返回第二个字符差值的ASCII码值 5
        System.out.println("15".compareTo("10"));
        //输出 1，第一个字符不同，返回第一个字符差值的ASCII码值 1
        System.out.println("35".compareTo("255"));
        // 输出 4，第一个字符不同，返回第一个字符差值的ASCII码值 4
        System.out.println("5".compareTo("10"));
        // 输出 -1，第一个字符不同，返回第一个字符差值的ASCII码值 -1
        System.out.println("15".compareTo("25"));
    }

//将二维字符数组转化成String，用到的String.copyValueOf(char[])的
	public List<String> char2List(char[][] path){
        LinkedList<String> list = new LinkedList<>();
        for (char[] ch : path) {
            list.add(String.copyValueOf(ch));
        }
        return list;
    }

2 经典力扣题

2.1 全排列问题

2.1.1 没有重复元素的全排列

剑指 Offer II 083. 没有重复元素集合的全排列==46. 全排列

给定一个不含重复数字的整数数组 nums ，返回其 所有可能的全排列 。可以 按任意顺序 返回答案。

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

	List<List<Integer>> res;
    public List<List<Integer>> permute(int[] nums) {
//        1.创建存放结果集的List
        res = new LinkedList<>();
        LinkedList<Integer> track = new LinkedList<>();
        trackBack(nums,track);
        return res;
    }

    public void trackBack(int[] num, LinkedList<Integer> list){
//        1.结束条件，全排列，全部元素都在里面
        if(list.size()==num.length){
            //为什么要 new LinkedList<>(list)，因为list是一个引用，不创建新的话，还是会
            res.add(new LinkedList<>(list));
            return;
        }
//        2.确定遍历的集合时全部元素
        for (int i = 0; i < num.length; i++) {
//            3.首先需要将已经在列表中的元素排除
            if(list.contains(num[i])){
                continue;
            }
//            4.做出选择
            list.add(num[i]);
//            5.继续递归下去
            trackBack(num,list);
//            6.撤销选择
            list.removeLast();
        }
    }

2.1.2 含重复元素的递归全排列

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

思路：这里所给元素是重复的，所以如何去处理重复元素

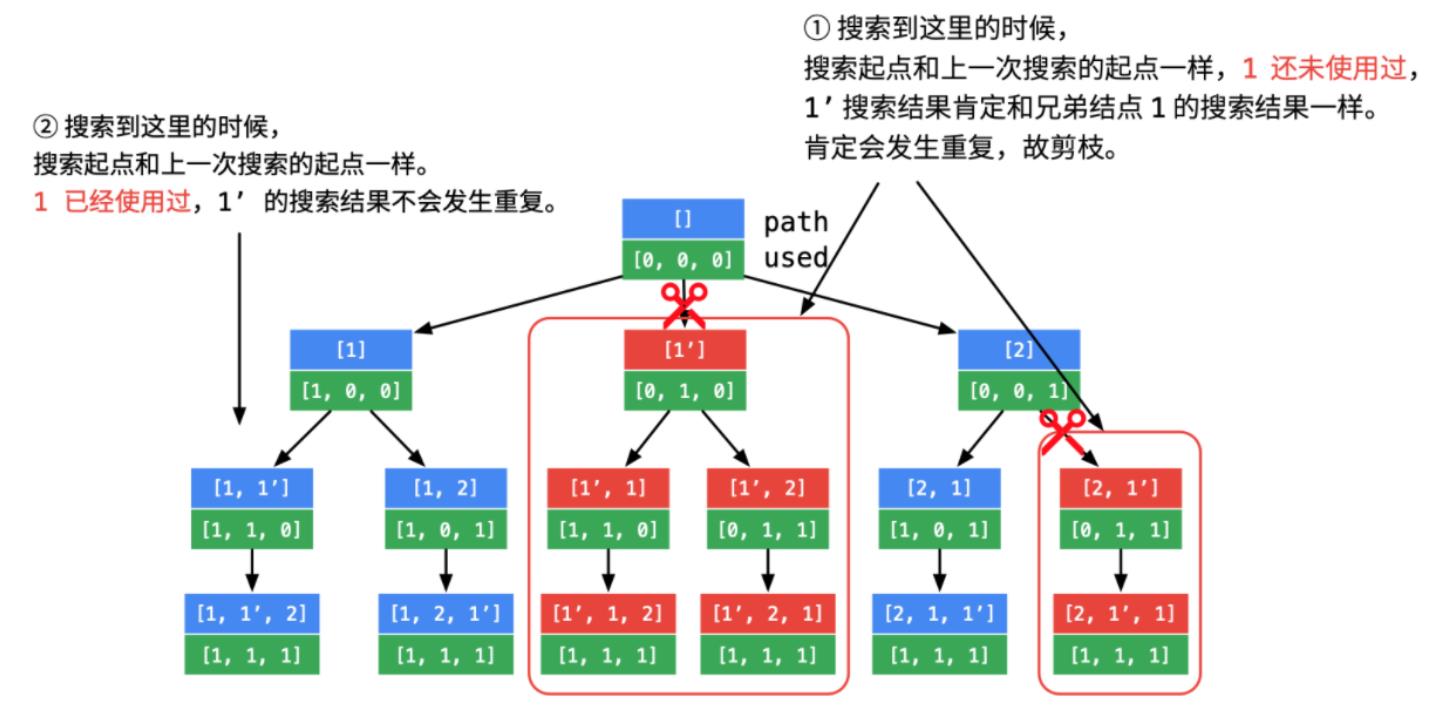
① 进行排序，那么相同的元素就会排在一起

	if(i>0 && nums[i]==nums[i-1] && !isVisit[i-1]){
         continue;
     }
  • 保证相同的元素只会在根节点回溯时只回溯一次nums[i]==nums[i-1]，如图①
  • 为了避免[1,1,2]这种情况被剪枝，再加一个限制条件!isVisit[i-1]，既前一个元素不在遍历的路径上

② 对使用过的元素进行标记

	List<List<Integer>> ans;
    boolean[] isVisit;
    public List<List<Integer>> permuteUnique(int[] nums) {
//        1.前期处理
        if(nums==null || nums.length==0){
            return null;
        }
        ans = new LinkedList<>();
        LinkedList<Integer> path = new LinkedList<>();
//        2.排序
        Arrays.sort(nums);
//        3.回溯穷举
        trackBack2(nums,path);
        return ans;
    }

    public void trackBack(int[] nums,LinkedList<Integer> path){
//        1.结束条件，找到一组合格的解
        if(path.size()==nums.length){
            ans.add(new LinkedList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
//            1.首先需要将已经在列表中的元素排除
            if(isVisit[i]){
                continue;
            }
//            2.重复数字只会在第一次出现时填入一次，[1 1 2]这种情况还必须加上前一个元素没有被选上的条件
            if(i>0 && nums[i]==nums[i-1] && !isVisit[i-1]){
                continue;
            }
//            3.做出选择
            path.add(nums[i]);
            isVisit[i] = true;
//            4.回溯
            trackBack(nums,path);
//            5.撤销选择
            path.removeLast();
            isVisit[i] = false;
        }
    }

2.2 子集问题

2.2.1 不含重复元素的子集

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

	List<List<Integer>> res;
    public List<List<Integer>> subsets(int[] nums) {
        res = new LinkedList<>();
        if(nums==null || nums.length==0){
            res.add(new LinkedList<>());
            return res;
        }
        LinkedList<Integer> set = new LinkedList<>();
        trackBack(nums,0,set);
        return res;
    }

    public void trackBack(int[] num, int start, LinkedList<Integer> set){
//        1.因为是子集，所以结束条件不是长度，而是直接入结果集
        res.add(new LinkedList<>(set));
//        2.起始位置保证了不会有重复元素
        for (int i = start; i < num.length ; i++) {
            set.add(num[i]);
//            3.注意！！！这里是 i+1 而不是 start+1，找了半天的错误找不到
            trackBack(num,i+1,set);
            set.removeLast();
        }
    }

2.2.2 含重复元素的子集个数

90. 子集 II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

思路：

① 排序，使相同的元素在一堆

② 同全排列的思考，标记，当前一个相同的元素没选中，并且当前元素等于前一个元素，那么剪枝就可以去重了

	List<List<Integer>> ans;
    boolean[] isVisit;
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        ans = new LinkedList<>();
        isVisit = new boolean[nums.length];
        if(nums==null || nums.length==0){
            ans.add(new LinkedList<>());
            return ans;
        }
        Arrays.sort(nums);
        LinkedList<Integer> path = new LinkedList<>();
        backTrack(nums,0,path);
        return ans;
    }

    public void backTrack(int[] nums,int start,LinkedList<Integer> path){
        ans.add(new LinkedList<>(path));
        for (int i = start; i < nums.length; i++) {
//          1.思路同全排列，剪枝去重
            if(i>0 && nums[i]==nums[i-1] && !isVisit[i-1]){
                continue;
            }
            path.add(nums[i]);
            isVisit[i] = true;
            backTrack(nums,i+1,path一文通数据结构与算法之——数组+常见题型与解题策略+Leetcode经典题


 一文通数据结构与算法之——链表+常见题型与解题策略+Leetcode经典题


 一文通数据结构与算法之——二叉树+常见题型与解题策略+Leetcode经典题


 一文通数据结构与算法之——图+常见题型与解题策略+Leetcode经典题


 一网打尽！二分查找解题模版与题型全面解析


 回溯算法思想回溯算法解题模板与回溯算法题目索引（不断更新）