Halo2 学习笔记——Gadgets 之 SHA-256
Posted mutourend
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Halo2 学习笔记——Gadgets 之 SHA-256相关的知识，希望对你有一定的参考价值。
1. 引言
SHA-256详细说明参见 NIST FIPS PUB 180-4。
与该说明书不同之处在于，Halo2中使用 ⊞ \\boxplus ⊞ 来表示addition modulo 2 32 2^{32} 232， + + + 来表示field addition， ⊕ \\oplus ⊕ 来表示 XOR。
2. Gadget interface
SHA-256用8个32-bit变量来维护state，其输入为512-bit blocks，内部会将这些blocks切分为32-bit chunks，因此设计了SHA-256 gadget来consume input in 32-bit chunks。
3. Chip instructions
SHA-256 gadget需要具有如下指令的chip：
# extern crate halo2;
# use halo2::plonk::Error;
# use std::fmt;
#
# trait Chip: Sized {}
# trait Layouter<C: Chip> {}
const BLOCK_SIZE: usize = 16;
const DIGEST_SIZE: usize = 8;
pub trait Sha256Instructions: Chip {
/// Variable representing the SHA-256 internal state.
type State: Clone + fmt::Debug;
/// Variable representing a 32-bit word of the input block to the SHA-256 compression
/// function.
type BlockWord: Copy + fmt::Debug;
/// Places the SHA-256 IV in the circuit, returning the initial state variable.
fn initialization_vector(layouter: &mut impl Layouter<Self>) -> Result<Self::State, Error>;
/// Starting from the given initial state, processes a block of input and returns the
/// final state.
fn compress(
layouter: &mut impl Layouter<Self>,
initial_state: &Self::State,
input: [Self::BlockWord; BLOCK_SIZE],
) -> Result<Self::State, Error>;
/// Converts the given state into a message digest.
fn digest(
layouter: &mut impl Layouter<Self>,
state: &Self::State,
) -> Result<[Self::BlockWord; DIGEST_SIZE], Error>;
}
这些指令用于strike a balance between the reusability of the instructions and the scope for chips to internally optimise them。特别地，考虑将compression function 按其组成部分切分为 Ch, Maj等等，并提供a compression function gadget 来实现the round logic。但是，这将阻止chips from using relative references between the various parts of a compression round。采用一个指令来实现所有的compression rounds则类似于the Intel SHA extensions——提供了一个指令来运行多个compression rounds。
4. 16-bit table chip for SHA-256
Halo2中的chip for SHA-256实现是基于a single 16-bit lookup table的。其最少需要 2 16 2^{16} 216 circuit rows，从而也适合用于larger circuits中。
Halo2中定义的最大constraint degree为 9 9 9，将支持进行constraining carries 和 “small pieces” to a range of up to { 0..7 } \\{0..7\\} {0..7} in one row。
4.1 Compression round
一共有64 compression rounds。每一轮的输入为32-bit values
A
,
B
,
C
,
D
,
E
,
F
,
G
,
H
A, B, C,D,E,F,G,H
A,B,C,D,E,F,G,H，并执行如下操作：
C
h
(
E
,
F
,
G
)
=
(
E
∧
F
)
⊕
(
¬
E
∧
G
)
M
a
j
(
A
,
B
,
C
)
=
(
A
∧
B
)
⊕
(
A
∧
C
)
⊕
(
B
∧
C
)
=
c
o
u
n
t
(
A
,
B
,
C
)
≥
2
Σ
0
(
A
)
=
(
A
⋙
2
)
⊕
(
A
⋙
13
)
⊕
(
A
⋙
22
)
Σ
1
(
E
)
=
(
E
⋙
6
)
⊕
(
E
⋙
11
)
⊕
(
E
⋙
25
)
H
′
=
H
+
C
h
(
E
,
F
,
G
)
+
Σ
1
(
E
)
+
K
t
+
W
t
E
n
e
w
=
r
e
d
u
c
e
6
(
H
′
+
D
)
A
n
e
w
=
r
e
d
u
c
e
7
(
H
′
+
M
a
j
(
A
,
B
,
C
)
+
Σ
0
(
A
)
)
\\begin{array}{rcl} Ch(E, F, G) &=& (E \\wedge F) \\oplus (¬E \\wedge G) \\\\ Maj(A, B, C) &=& (A \\wedge B) \\oplus (A \\wedge C) \\oplus (B \\wedge C) \\\\ &=& count(A, B, C) \\geq 2 \\\\ \\Sigma_0(A) &=& (A ⋙ 2) \\oplus (A ⋙ 13) \\oplus (A ⋙ 22) \\\\ \\Sigma_1(E) &=& (E ⋙ 6) \\oplus (E ⋙ 11) \\oplus (E ⋙ 25) \\\\ H' &=& H + Ch(E, F, G) + \\Sigma_1(E) + K_t + W_t \\\\ E_{new} &=& reduce_6(H' + D) \\\\ A_{new} &=& reduce_7(H' + Maj(A, B, C) + \\Sigma_0(A)) \\end{array}
Ch(E,F,G)Maj(A,B,C)Σ0(A)Σ1(E)H′EnewAnew========(E∧F)⊕(¬E∧G)(A∧B)⊕(A∧C)⊕(B∧C)count(A,B,C)≥2(A⋙2)⊕(A⋙13)⊕(A⋙22)(E⋙6)⊕(E⋙11)⊕(E⋙25)H+Ch(E,F,G)+Σ1(E)+Kt+Wtreduce6(H′+D)reduce7(H′+Maj(A,B,C)+Σ0(A))
其中
r
e
d
u
c
e
i
reduce_i
reducei 必须handle a carry
0
≤
c
a
r
r
y
<
i
0\\leq carry <i
0≤carry<i。
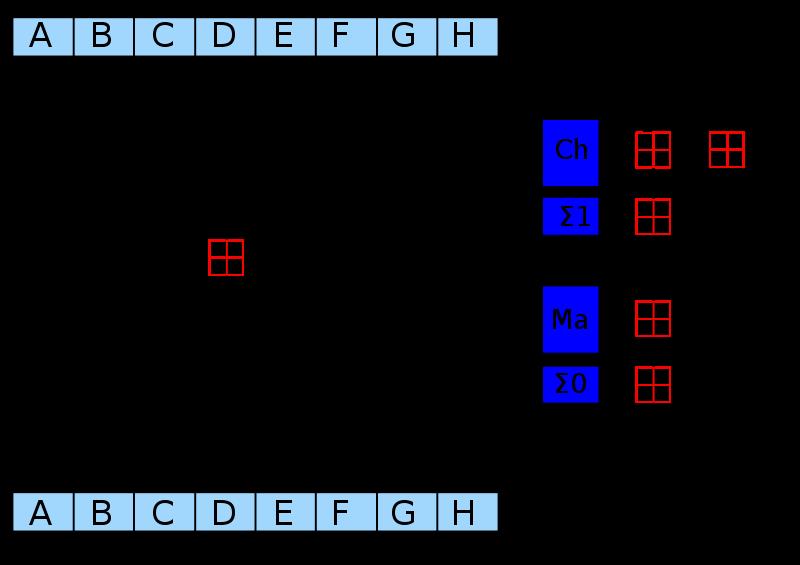
定义
s
p
r
e
a
d
\\mathtt{spread}
spread 为 a table mapping a
16
16
16-bit input to an output interleaved with zero bits。不需要一个单独的table来进行 range checks 因为可复用
s
p
r
e
a
d
\\mathtt{spread}
spread。
4.2 Modular addition
对于addition modulo
2
32
2^{32}
232：
a
⊞
b
=
c
a \\boxplus b = c
a⊞b=c
将其切分为
16
16
16-bit chunks表示为：
(
a
L
:
Z
2
16
,
a
H
:
Z
2
16
)
⊞
(
b
L
:
Z
2
16
,
b
H
:
Z
2
16
)
=
(
c
L
:
Z
2
16
,
c
H
:
Z
2
16
)
(a_L : \\mathbb{Z}_{2^{16}}, a_H : \\mathbb{Z}_{2^{16}}) \\boxplus (b_L : \\mathbb{Z}_{2^{16}}, b_H : \\mathbb{Z}_{2^{16}}) = (c_L : \\mathbb{Z}_{2^{16}}, c_H : \\mathbb{Z}_{2^{16}})
(aL:Z216,aH:Z216)⊞(bL:Z216,bH:Z216)=(cL:Z216,cH:Z216)
使用field addition重组表示为：
c
a
r
r
y
⋅
2
32
+
c
H
⋅
2
16
+
c
L
=
(
a
H
+
b
H
)
⋅
2
16
+
a
L
+
b
L
\\mathsf{carry} \\cdot 2^{32} + c_H \\cdot 2^{16} + c_L = (a_H + b_H) \\cdot 2^{16} + a_L + b_L
caHalo2 学习笔记——设计之Proving system之Lookup argument
Halo2 学习笔记——设计之Proving system之Permutation argument