数据结构 --- [二分搜索树 (Java)]
Posted 小智RE0
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构 --- [二分搜索树 (Java)]相关的知识,希望对你有一定的参考价值。
🚀树是一种数据结构,它是由n(n≥1)个有限节点组成一个具有层次关系的集合.
==>树(百度百科)
- 二叉树也是动态数据结构,它是天然的递归结构;
- 具有唯一的根节点;也就是顶层的节点,
- 每个节点最多只有两个子节点,即
左子树和右子树; - 而每个节点最多可以有一个父节点.
- 每个节点的左子树,右子树也是二叉树结构
- 满二叉树是指 除了位于最后一层的
叶子节点没有子节点,其余节点都有两个子节点的树.
(一个层数为k 的满二叉树总结点数为:2k-1)
(第k层上的结点数为:2k-1)
(一个层数为k的满二叉树的叶子结点个数(也就是最后一层):2k-1)
(层数为k的满二叉树的非叶子结点个数(除了最后一层) : 2k-1 -1) - 注意二叉树不一定是满的
二分搜索树是一种比较特殊的二叉树;
- 左子树都是小于父级节点的;
- 右子树都是大于父级节点的.
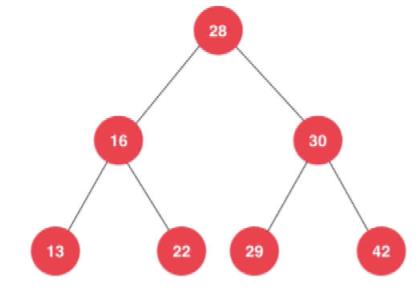
二分搜索树的实现
先把二分搜索树的基本结构定义出来;
由于二分搜索树的比较特性,所以这里泛型就需要继承Comparable接口的泛型类
public class BinarySearchTree<T extends Comparable<T>> {
//定义内部类结点;
class Node{
T val;
//左子树,右子树;
Node leftNode;
Node rightNode;
public Node(T val){
this.val=val;
this.leftNode=null;
this.rightNode=null;
}
}
//定义树的根结点;
private Node root;
//定义树结点的个数;
private int size;
//初始化二叉树;
public BinarySearchTree(){
this.root=null;
this.size=0;
}
//判空;
public boolean isEmpty(){
return this.root==null;
}
}
添加元素的方法实现
需要注意的是每个节点都可以作为根节点
//添加元素;
public void add(T ele){
//每次将创建的根节点返回;
root = add(root,ele);
//元素个数增加;
this.size+=1;
}
//递归添加元素的底层;
private Node add(Node root, T ele) {
//不存在就创建;
if(root ==null){
Node node=new Node(ele);
return node;
}
//添加的元素和之前的根节点进行比较;
if(ele.compareTo(root.val)>0){
root.rightNode = add(root.rightNode,ele);
}else{
root.leftNode = add(root.leftNode,ele);
}
return root;
}
查询二叉树是否包含指定元素的方法实现;
//查询元素;
public Node contains(T ele){
//若二叉树都为空了,不用进入查询;
if(root == null){
return null;
}
return contains(root,ele);
}
//查询元素的底层;
private Node contains(Node root, T ele) {
//递归的结束点,即查到最后一层的叶子节点时,
if(root == null){
return null;
}
//将 当前根节点 的值存储;
T val=root.val;
if(ele.compareTo(val)==0){
return root;
//若指定的元素值大于节点,就在右子树开始查;否则去左子树查询;
}else if(ele.compareTo(val)>0){
return contains(root.rightNode,ele);
}else{
return contains(root.leftNode,ele);
}
}
中序遍历
依次顺序为 : 左子树 ==> 中间节点 ==> 右子树
例如:13==>16==>22==>28==>29==>30==>42

中序遍历方法实现;
//中序遍历;
public List<T> middleOrder(){
//若二叉树为空,则直接返回null空值;
if(root==null){
return null;
}
//遍历的结果存入集合中;
List<T> list=new ArrayList<>();
middleOrder(root,list);
return list;
}
//中序遍历底层;
private void middleOrder(Node root, List<T> list) {
//递归结束点,若到达最后一层的叶子节点就停止;
if(root==null){
return;
}
//中序遍历= 先遍历左子树 ==> 获取中间结点 ==> 遍历右子树
middleOrder(root.leftNode,list);
list.add(root.val);
middleOrder(root.rightNode,list);
}
前序遍历
依次顺序为 : 中间节点 ==> 左子树 ==> 右子树
例如: 26==> 16 ==> 13 ==> 22 ==> 30 ==>29 ==>42

前序遍历方法实现
//前序遍历;
public List<T> frontOrder(){
//若二叉树为空,则直接返回null空值;
if(root==null){
return null;
}
//遍历的结果存入集合中;
List<T> list=new ArrayList<>();
frontOrder(root,list);
return list;
}
//前序遍历底层;
private void frontOrder(Node root, List<T> list) {
//递归结束点,若到达最后一层的叶子节点就停止;
if(root==null){
return;
}
//前序遍历= 先获取中间节点 ==> 遍历左子树 ==>遍历右子树
list.add(root.val);
frontOrder(root.leftNode,list);
frontOrder(root.rightNode,list);
}
后序遍历
依次顺序为 : 左子树 ==> 右子树 ==> 中间节点
例如: 13 == > 22 == > 16==> 29 ==> 42 ==> 30 ==> 28

后序遍历实现;
//后序遍历;
public List<T> latterOrder(){
//若二叉树为空,则直接返回null空值;
if(root==null){
return null;
}
//遍历的结果存入集合中;
List<T> list=new ArrayList<>();
latterOrder(root,list);
return list;
}
//后序遍历底层;
private void latterOrder(Node root, List<T> list) {
//递归结束点,若到达最后一层的叶子节点就停止;
if(root==null){
return;
}
//后序遍历= 先遍历左子树 ==> 遍历右子树 ==> 获取中间节点;
latterOrder(root.leftNode,list);
latterOrder(root.rightNode,list);
list.add(root.val);
}
层序遍历
从树的第一层开始,一层一层第取得其中的节点;
例如:28 == > 16 ==>30 == > 13 ==> 22 ==> 29 ==> 42
- 首先把 28 放入一个空队列中,然后把
28 从队首取出,判断队列是否为空;不为空,继续操作; - 由于 28 有左子树右子树,就把 16 和 30 依次从队尾放入队列;
- 将
16 从队首取出,判断队列是否为空;不为空,继续操作; - 由于 16 具有左子树和右子树,那么就把 13 和 22 依次从队尾放入队列;
- 这时将
30 从队首取出,判断队列是否为空;不为空,继续操作; - 由于 30 具有左子树和右子树,就把 29 和 42 依次从队尾放入队列;
- 将
13 从队首取出,判断队列是否为空;不为空,继续操作; - 将
22从队首取出,判断队列是否为空,不为空,继续操作; - 将
29从队首取出,判断队列是否为空,不为空,继续操作; - 将
42从队首取出,判断队列是否为空,不为空,继续操作;

层序遍历实现;
//层序遍历;
public List<T> levelOrder(){
//最终使用数组存储遍历结果;
List<T> list=new ArrayList<>();
//若此树不为空;就进行遍历操作;
if(root!=null){
//定义队列把根节点从队尾加入;
Queue<Node> queue=new LinkedList<>();
queue.add(root);
//只要队列不为空;就继续操作;
while(!queue.isEmpty()){
//从队首取出节点;
Node node= queue.poll();
//将取出的节点存入数组;
list.add(node.val);
//若取出的节点存在左子树或右子树,就存入队列;
if(node.leftNode!=null){
queue.offer(node.leftNode);
}
if(node.rightNode!=null){
queue.offer(node.rightNode);
}
}
}
return list;
}
查询二分搜索树的最大元素和最小元素
最小的元素就是最左边的叶子节点;
最大的元素就是最右边的叶子节点;
使用底层循环的方式实现;
//使用循环的方式查找最大元素;
public T findMaxNode(){
if(root == null){
return null;
}
//先将根节点作为操作节点;
Node curNode=root;
//只要操作节点的右子树不为空,就不停止循环;
while(curNode.rightNode!=null){
//一直取到最右边的节点,即最大节点;
curNode=curNode.rightNode;
}
return curNode.val;
}
//使用循环的方式查找最小元素;
public T findMinNode(){
if(root == null){
return null;
}
//先将根结点作为操作节点;
Node curNode=root;
//只要操作节点的左子树不为空,就不停止循环;
while(curNode.leftNode!=null){
//一直取到最左边的节点;即最小节点;
curNode=curNode.leftNode;
}
return curNode.val;
}
使用底层递归的方式实现
//递归方式寻找最大元素;
public T findMaxNodeRecurve(){
if(root == null){
return null;
}
return findMaxNodeRecurve(root).val;
}
//递归方式寻找最大元素的底层实现;
private Node findMaxNodeRecurve(Node root) {
//递归的结束点;
if(root.rightNode == null){
return root;
}
return findMaxNodeRecurve(root.rightNode);
}
//递归方式寻找最小元素;
public T findMinNodeRecurve(){
if(root == null){
return null;
}
return findMinNodeRecurve(root).val;
}
//递归方式寻找最小元素的底层实现;
private Node findMinNodeRecurve(Node root) {
//递归结束点;
if(root.leftNode==null){
return root;
}
return findMinNodeRecurve(root.leftNode);
}
删除最小节点
//删除最小节点;
public void removeMinNode(){
//找到最小元素;
T minNode = findMinNodeRecurve();
if(minNode == null){
System.out.println("空树不用删除");
return;
}
System.out.println("删除的最小节点是=>"+minNode);
// 删除后的树的根结点挂到原树上;
root = removeMinNode(root);
this.size-=1;
}
//删除最小节点的底层实现;
private Node removeMinNode(Node node) {
//若到达最左边,即停止;
if(node.leftNode == null){
//右子树挂到删除节点处;
Node n= node.rightNode;
node.rightNode = null;
return n;
}
//递归;
node.leftNode = removeMinNode(node.leftNode);
return node;
}
删除最大节点
//删除最大节点;
public void removeMaxNode(){
//先找到最大节点;
T maxNodeRecurve = findMaxNodeRecurve();
if(maxNodeRecurve==null){
System.out.println("空树不用删除");
}
System.out.println("删除的最大节点是=>"+maxNodeRecurve);
//删除后的返回值节点连到原节点后;
root = removeMaxNode(root);
this.size -= 1;
}
//删除最大节点的底层实现;
private Node removeMaxNode(Node node) {
//到达最右边就停止;
if(node.rightNode == null){
Node n = node.leftNode;
node.leftNode = null;
return n;
}
//递归;
node.rightNode = removeMaxNode(node.rightNode);
return node;
}
删除指定值的节点
/**
* 删除指定结点;
* @param val
* @return
*/
public T removeAssignVal(T val){
if(root == null){
System.out.println("空树不用删除");
return null;
}
//先去找是否存在; 要去新建方法;
Node node = findAssignNode(root,val);
//是否找到;
if(node!=null){
//删除后的剩余结点挂到根结点之后;
root = removeAssignVal(root,val);
//元素个数减少;
this.size-=1;
return node.val;
}
return null;
}
/**
* 删除指定结点的底层实现;在根结点为node的二分树中删除指定结点;
* @param node
* @param val
* @return
*/
private Node removeAssignVal(Node node, T val) {
//找到结点时;
if(node.val.compareTo(val) == 0){
//第一种情况==> 该删除结点的左树为空;
if(node.leftNode == null){
//删除当前的结点后;把原来后面的右子树挂到删了结点的位置;
Node RNode = node.rightNode;
node.rightNode= null;
return RNode;
}
//第二种情况,右树为空;
else if(node.rightNode == null){
//删除当前的结点后;把原来后面的左子树挂到删了结点的位置;
Node LNode = node.leftNode;
node.leftNode = null;
return LNode;
}else {
//情况三; 左树 右树 都不为空时,可以选择找前驱结点(左子树那块区域的最大值) 或 后继结点(右子树那块区域的最小值)代替删除结点;
//这里选择找后继节点;
Node minR = findMinNodeRecurve(node.rightNode);
Node minRNode= removeMinNode(node.rightNode);
//后继节点放到删除的结点位置;
minR.leftNode = node.leftNode;
minR.rightNode = minRNode;
node.leftNode = null;
node.rightNode =null;
return minR;
}
}
//递归;
//找结点时,若当前的根结点比指定的值还大,就去左边找; 否则去右边找;
if(node.val.compareTo(val) > 0){
node.leftNode = removeAssignVal(node.leftNode,val);
}else {
node.rightNode = removeAssignVal(node.rightNode,val);
}
return node;
}
/**
* 由根结点开始寻找指定的元素;
* @param node
* @param val
* @return
*/
private Node findAssignNode(Node node, T val) {
//没找到就返回null值;
if(node==null){
return null;
}
//若当前结点就是指定的值;
if(node.val.compareTo(val)==0){
return node;
}
//当前的根结点比指定的值还大,根据二分搜索树性质,越小的 就在左子树去找;
else if(node.val.compareTo(val)>0){
//去左子树查询;
return findAssignNode(node.leftNode,val