从计算机二进制认识哈夫曼编码等长编码变长编码

Posted 2021-10-21 Roninaxious

• 1.计算机是如何存储信息的？
• 2.等长编码
• • 2.1.等长编码的优点
  • 2.1.等长编码的缺点
• 3.变长编码
• • 3.1.变长编码的缺点
  • 3.1.变长编码的优点
• 4.哈夫曼编码
• • 4.1.哈夫曼编码的生成过程

---

1.计算机是如何存储信息的？

面对数不尽的中文和英文，你能识别，但计算机是无法识别的。我们都知道计算机运行过程中是需要电力进行支持的，所以计算机只能识别低电平和高电平(也就是0和1）。

因此我们在计算机中看到的一切文字、图片、视频等等，底层都是使用二进制进行存储的。

所以说从人能识别的图片文字到计算机能够识别的二进制，这个过程叫做编码。

2.等长编码

想必都知道ASCII，在ACSII中将一个字符表示成8为特定的二进制数


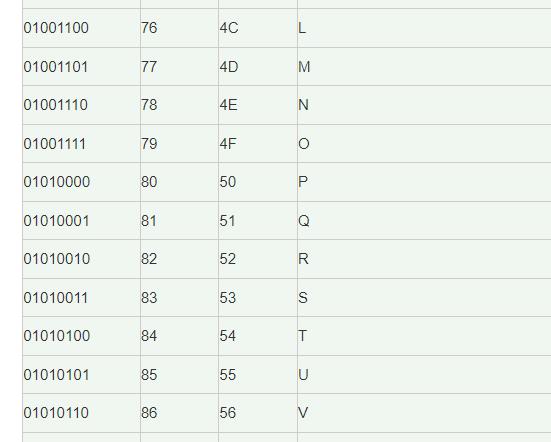
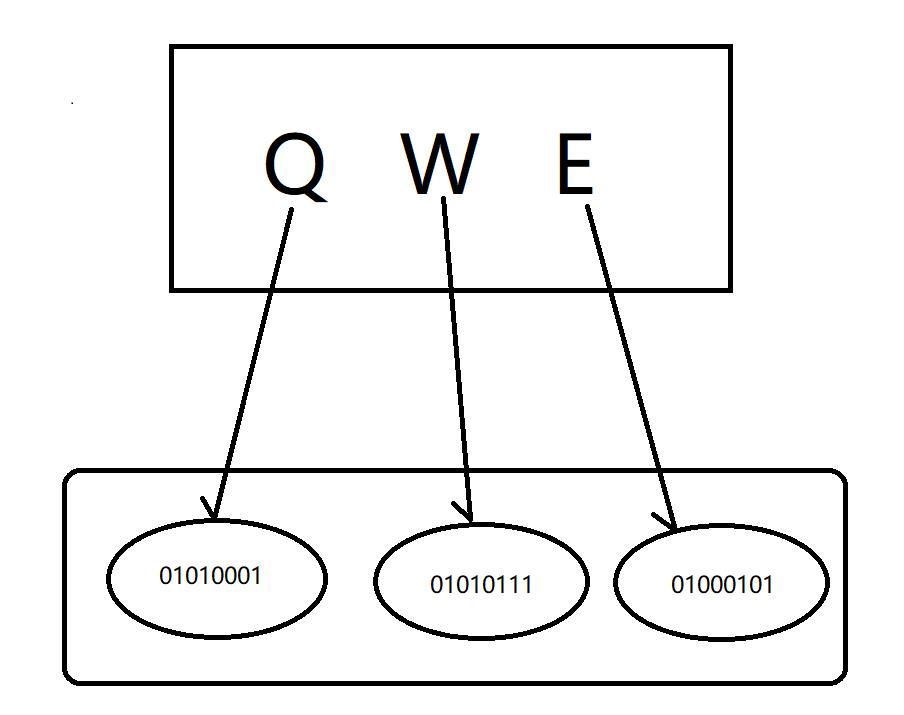
根据上述，ASCII将字符表示为8位特定的二进制数，所以ASCII是一种等长编码。

2.1.等长编码的优点

这个等长编码的优点很明显，每个字符都有对应的二进制编码，且长度是固定。所以很容易设计，也很方便读写。

2.1.等长编码的缺点

计算机的存储及网络带宽是有限的，等长编码的缺点就是编码结果太长，很容易占用太多的计算机资源

字符	编码
1	0000 0001
2	0000 0010
3	0000 0011
4	0000 0100

(ASCII编码)对于上方表格中的字符编码表，我们可以计算出它的编码结果length = 32；实际上它的高位都浪费了。

3.变长编码

如下表，我自定义字符编码表

字符	编码
1	1
2	10
3	11
4	100

通过计算它的编码结果length = 7；

编码长度缩小了(32 - 7 ) / 32 = 78.1%

3.1.变长编码的缺点

根据上方我自定义的字符编码表，字符2是字符4的前缀，字符1是字符3的前缀。假设有编码结果为11100100，当我们根据编码表进行数据还原时。

#假设V表示扫描移动指针，假设原数据为“344”

1.当扫描到第一位1时，根据编码表直接匹配到了字符‘1’
2.我们本来的原数据第一个字符为“3”。
造成这个原因就是一个字符的编码刚好是另外一个字符的前缀，多义性是变长编码的缺点，所以如何设计编码很重要

3.1.变长编码的优点

这个优点就很明显了，编码长度得到了大幅的缩小。

4.哈夫曼编码

哈夫曼编码(Huffman Coding)，是由麻省理工学院的哈夫曼博所发明，这个编码方式解决了变长编码多义性的问题。

哈夫曼编码并非是一套固定的编码，它是根据给定的信息中每个字符出现的频率，动态地生成编码表。

4.1.哈夫曼编码的生成过程

假如一段信息里只有A，B，C，D，E，F这6个字符，他们出现的次数依次是2次，3次，7次，9次，18次，25次，如何设计对应的编码呢？

我们不妨把这6个字符当做6个叶子结点，把字符出现次数当做结点的权重，以此来生成一颗哈夫曼树：

算法系列之赫夫曼树的精解【构造流程及原理分析】:https://blog.csdn.net/Kevinnsm/article/details/120584098?spm=1001.2014.3001.5501

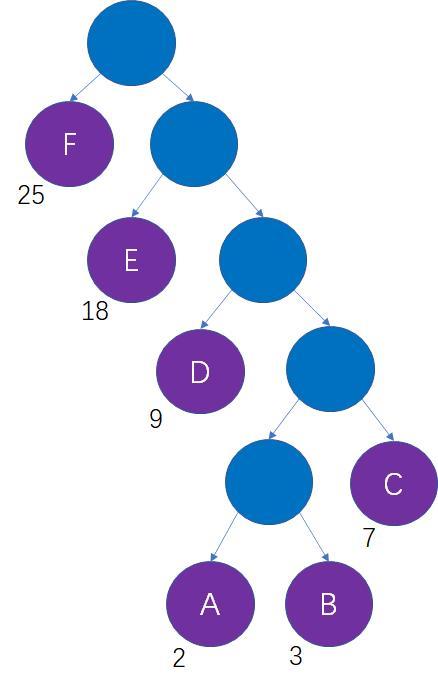
我们可以看出哈夫曼树有左右两个分支，计算机二进制有两种状态0和1，所以我们可以将其对应起来。

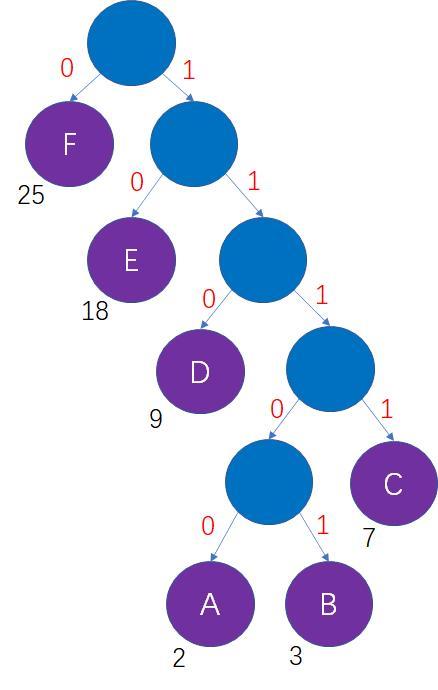
这样一来，从哈夫曼树的根结点到每一个叶子结点的路径，都可以等价为一段二进制编码：

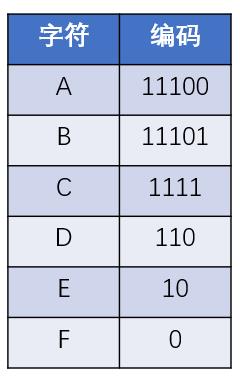
上述过程借助哈夫曼树所生成的二进制编码，就是哈夫曼编码。所以这种哈夫曼编码解决了两个重要的问题

1.不存在多义性
2.编码长度最小(哈夫曼树的特性,叶子结点的权重 X 路径长度之和最小)。