[人工智能-深度学习-15]:神经网络基础 - 常见优化器Optimizer及其算法 - 梯度下降法系列
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[人工智能-深度学习-15]:神经网络基础 - 常见优化器Optimizer及其算法 - 梯度下降法系列相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120589554
目录
2.1 什么是梯度下降法(Gradient Descent)
3.2 Nesterov accelerated gradient (NAG)
第1章 什么是优化算法
1.1 机器学习模型与优化算法在机器学习模型中的位置
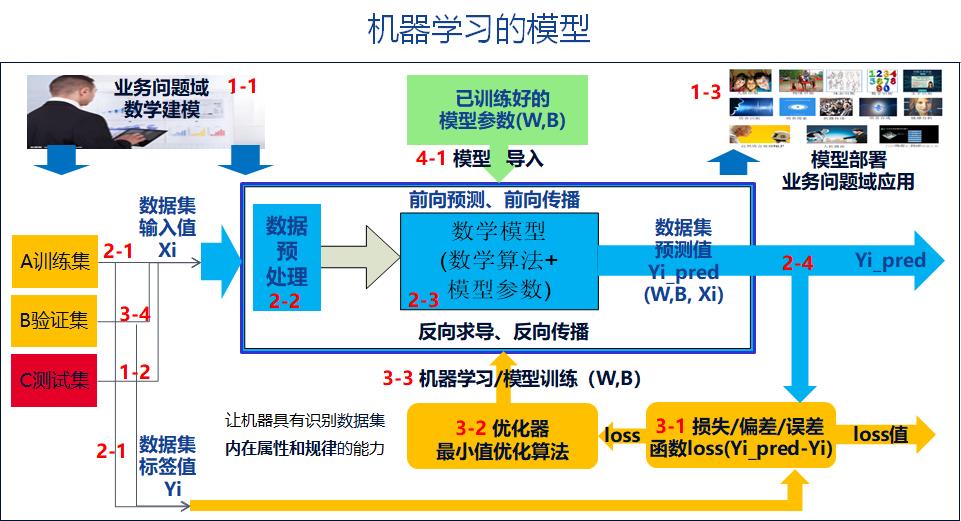
1.2 什么是优化器
优化器在深度学习反向传播过程中,指引损失函数(目标函数)的各个参数往正确的方向进行适合的更新,使得更新后的各个参数让损失函数(目标函数)值不断逼近全局最小。
换句话说:
优化器目的:就是针对指定的损失函数,通过计算机数值计算的方法,求损失函数最小值,以及在最小值时候的各种参数值(W, B参数)。
优化器手段:获取最小值的方法,是用计算机数值计算的方法,而不是用解析的方法。
1.3 什么是优化算法
寻找损失函数的最小值的方法有很多种,这些方法统称为优化算法。
优化器,就是定义某种算法,通过自动调整模型的参数,使得模型的预测值(输出值)与样本值之间的误差和是最小的,就求loss函数的最小值数值方法(计算机求极小值的算法)。
1.4 优化算法的核心思想
优化算法核心的手段就是:通过损失函数的导数(梯度),经过一次次的迭代,最终找到损失函数的最小值。
1.5 损失函数的几何图形
(1)一元函数的loss函数 (只有一个W参数)
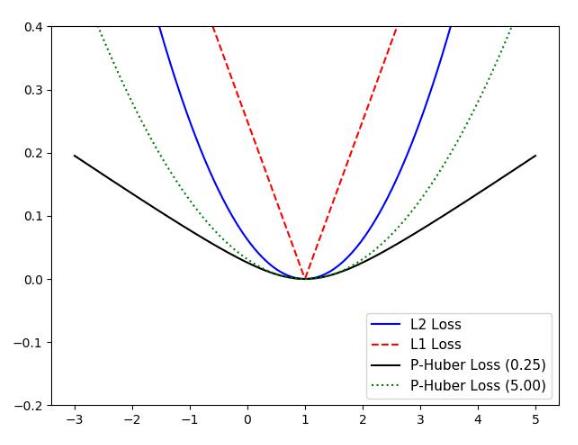
(2)多元函数的loss函数(多个W,B参数 )
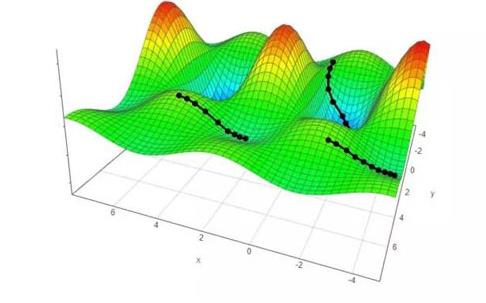
1.6 损失函数具有最小值的条件
并非所有的函数都有最小值,有最小值的函数,必须满足如下的条件:
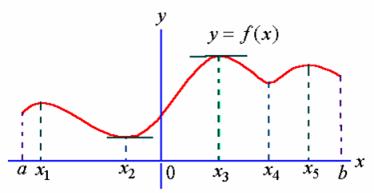
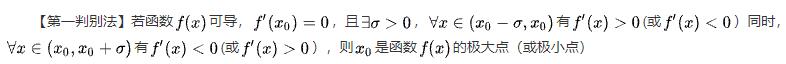
第2章 基础版梯度下降法:独立可变梯度
2.1 什么是梯度下降法(Gradient Descent)
梯度下降法是最基本的一类优化器,是当今最流行的优化(optimization)算法,亦是至今最常用的优化神经网络的方法。
基本策略可以理解为”在有限视距内寻找最快路径下山“,因此每走一步,参考当前位置最陡的方向(即梯度)进而迈出下一步。可以形象的表示为:
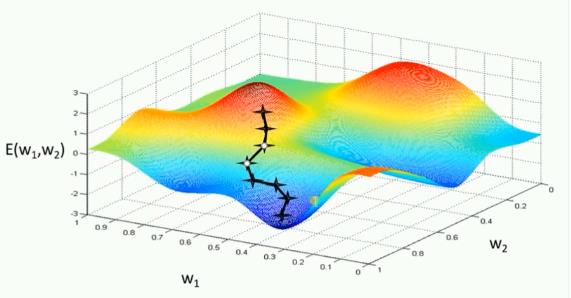
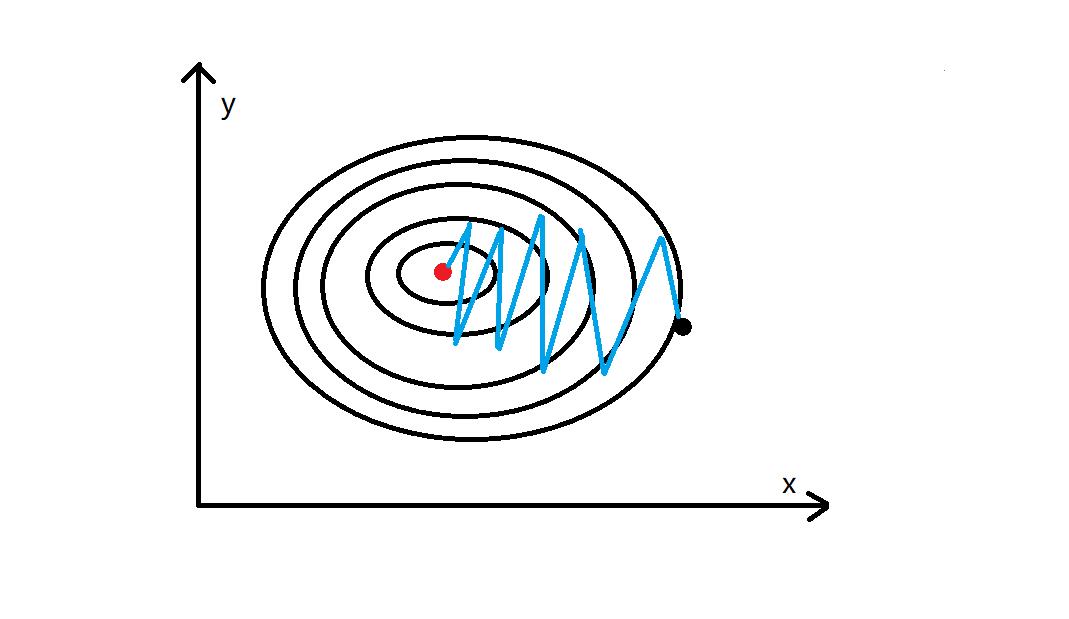
2.2 三种基本版梯度下降法
目前主要分为三种同源的梯度下降法,他们之前的区别在于一次迭代所需要的样本的数量
(1)标准梯度下降法(GD, Gradient Descent):每次迭代计算,使用所有的样本。
θ=θ−η⋅∇θJ(θ)
每迭代一步,都要用到训练集的所有数据,每次计算出来的梯度求平均
η代表学习率LR
(2)随机梯度下降法(SGD, Stochastic Gradient Descent),每次迭代计算,使用有限个随机样本。
θ=θ−η⋅∇θJ(θ;x(i);y(i))
通过每个样本来迭代更新一次,以损失很小的一部分精确度和增加一定数量的迭代次数为代价,换取了总体的优化效率的提升。增加的迭代次数远远小于样本的数量。
(3)批量梯度下降法(BGD, Batch Gradient Descent),每次迭代,所有样本中的一组样本。
θ=θ−η⋅∇θJ(θ;x(i:i+n);y(i:i+n))
为了避免SGD和标准梯度下降中存在的问题,对每个批次中的n个训练样本,这种方法只执行一次更新。【每次更新全部梯度的平均值】
第3章 加强版梯度下降法:带一阶动量的梯度
动量优化方法是在梯度下降法的基础上进行的改变,具有加速梯度下降的作用。
一般有标准动量优化方法Momentum、NAG(Nesterov accelerated gradient)动量优化方法。
3.1 Momentum
Momentum是模拟物理里动量的概念,积累之前的梯度(称为动量)来替代真正的梯度,并作为当的梯度。即在正确梯度方向上加速,并且抑制波动方向张的波动大小,在后期本次计算出来的梯度会很小,以至于无法跳出局部极值,Momentum方法也可以帮助跳出局部极值。
3.2 Nesterov accelerated gradient (NAG)
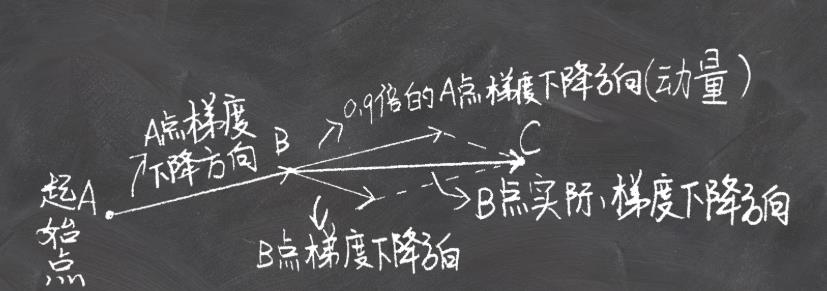
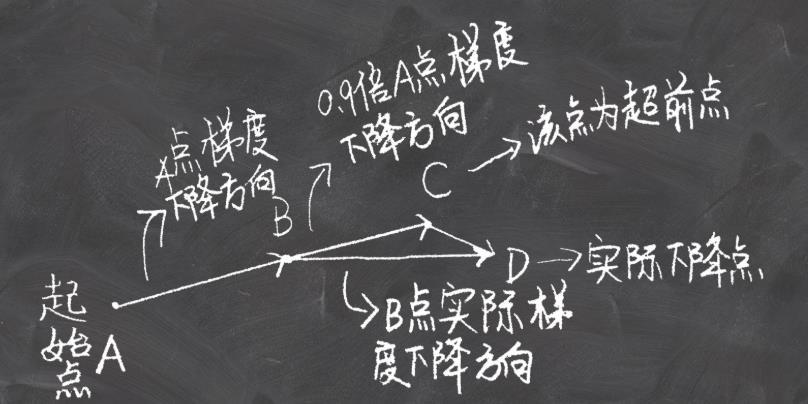
NAG方法收敛速度明显加快。波动也小了很多。
第4章 自适应学习率梯度下降法:学习率与自身的梯度自相关
前面的一系列优化算法有一个共同的特点,就是对于每一个参数都用相同的学习率进行更新。
但是在实际应用中各个参数的重要性肯定是不一样的,所以我们对于不同的参数要动态的采取不同的学习率,让目标函数更快的收敛。
4.1 Adagrad自适应梯度:历史平均
adagrad方法是将每一个参数的每一次迭代的梯度取平方累加再开方,用基础学习率除以这个数,来做学习率的动态更新。
这样一来,每一个参数的学习率就与他们自身的梯度有关系了,那么每一个参数的学习率就不一样了!也就是所谓的自适应学习率。
Adagrad的一大优势时可以避免手动调节学习率,比如设置初始的缺省学习率为0.01,然后就不管它,另其在学习的过程中自己变化。当然它也有缺点,就是它计算时要在分母上计算梯度平方的和,由于所有的参数平方【上述公式推导中并没有写出来是梯度的平方,感觉应该是上文的公式推导忘了写】必为正数,这样就造成在训练的过程中,分母累积的和会越来越大。这样学习到后来的阶段,网络的更新能力会越来越弱,能学到的更多知识的能力也越来越弱,因为学习率会变得极其小【就会提前停止学习】,为了解决这样的问题又提出了Adadelta算法。
4.2 Adadelta:平滑平均
Adagrad会累加之前所有的梯度平方,而Adadelta只累加固定大小的项【其实就是相当于指数滑动平均,只用了前多少步的梯度平方平均值】,并且也不直接存储这些项,仅仅是近似计算对应的平均值【这也就是指数滑动平均的优点】
第5章 带二阶动态的梯度下降法
5.1 RMSprop
RMSProp算法的全称叫 Root Mean Square Prop,
在上面的Momentum优化算法中,虽然初步解决了优化中摆动幅度大的问题。所谓的摆动幅度就是在优化中经过更新之后参数的变化范围,如下图所示,蓝色的为Momentum优化算法所走的路线,绿色的为RMSProp优化算法所走的路线。
为了进一步优化损失函数在更新中存在摆动幅度过大的问题,并且进一步加快函数的收敛速度,RMSProp算法对权重 W 和偏置 B 的梯度使用了微分平方加权平均数。

5.2 Adam
Adam = Adaptive + Momentum,顾名思义Adam集成了SGD的一阶动量和RMSProp的二阶动量。
SGD可以使用类似于物理中的动量来累积梯度,RMSProp可以使得收敛速度更快同时使得波动的幅度更小。Adam把它们的优点结合起来,以取得的更好的表现效果。
第6章 不同优化算法的直观比较
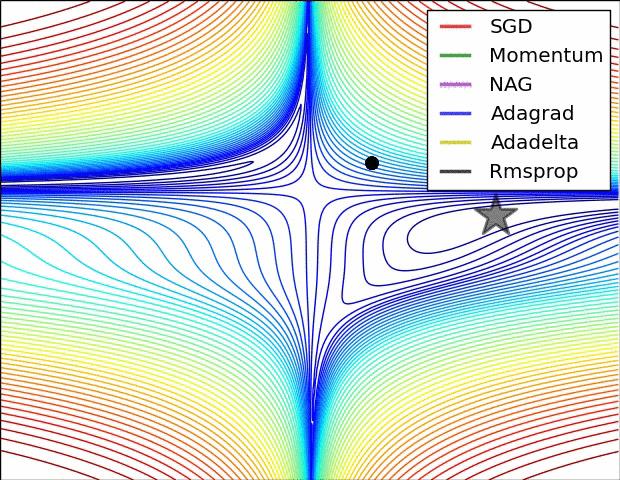
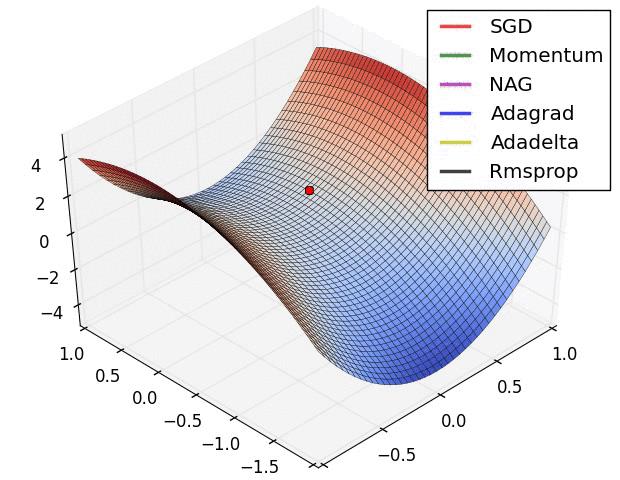
图 3 中,我们可以看到不同算法在损失面等高线图中的学习过程,它们均同同一点出发,但沿着不同路径达到最小值点。其中 Adagrad、Adadelta、RMSprop 从最开始就找到了正确的方向并快速收敛;SGD 找到了正确方向但收敛速度很慢;SGD-M 和 NAG 最初都偏离了航道,但也能最终纠正到正确方向,SGD-M 偏离的惯性比 NAG 更大。
图 4 展现了不同算法在鞍点处的表现。这里,SGD、SGD-M、NAG 都受到了鞍点的严重影响,尽管后两者最终还是逃离了鞍点;而 Adagrad、RMSprop、Adadelta 都很快找到了正确的方向。
不同算法,主要区别在于:
- 是否能够跳出极小值
- 收敛速度
提速又可以归纳为以下几个方面:
- 使用动量momentum来保持前进方向(velocity);
- 为每一维参数设定不同的学习率:进;在梯度连续性强的方向上加速前
- 用历史迭代的平均值归一化学习率:突出稀有的梯度。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120589554
以上是关于[人工智能-深度学习-15]:神经网络基础 - 常见优化器Optimizer及其算法 - 梯度下降法系列的主要内容,如果未能解决你的问题,请参考以下文章