POJ2398计算几何叉积判断点在线段左/右侧
Posted hesorchen
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了POJ2398计算几何叉积判断点在线段左/右侧相关的知识,希望对你有一定的参考价值。
题目
二维平面中有一个矩形,放入n块隔板,将矩形分成n+1个区域,隔板保证不相交且两端点在矩形的两条横向线段中。形如下图:
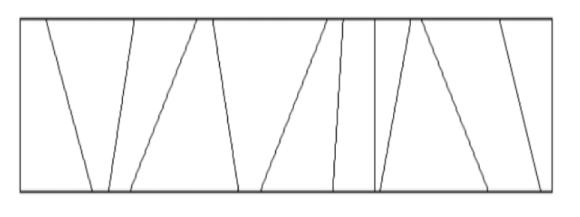
给出m个点,求包含t个点的区域数量。
求解思路
可以用叉积判断一个点在线段的左侧还是右侧。
O A ⃗ × O B ⃗ = ∣ O A ∣ × ∣ O B ∣ × sin θ \\vec{OA} \\times \\vec{OB}=|OA|\\times|OB|\\times \\sin\\theta OA×OB=∣OA∣×∣OB∣×sinθ
叉积为负,说明 θ 大 于 π \\theta 大于\\pi θ大于π
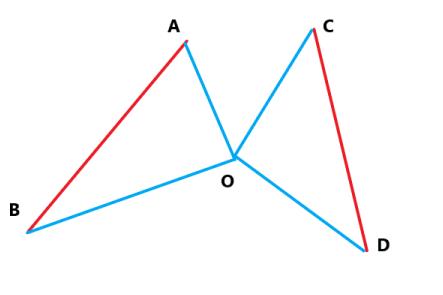
如果 O A ⃗ × O B ⃗ > 0 \\vec{OA} \\times \\vec{OB} >0 OA×OB>0 并且 O C ⃗ × O D ⃗ < 0 \\vec{OC} \\times \\vec{OD}<0 OC×OD<0,说明点O在区域ABCD内。
代码
#include <iostream>
#include <map>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e4 + 5;
struct node
{
int u, d;
bool operator<(const node temp) const
{
return u < temp.u;
}
} s[N];
int tong[N];
int ans[N];
int n, m, sx, sy, ex, ey;
typedef struct Point
{
double x, y;
} Vector;
bool check(Vector A, Vector B)
{
if (A.x * B.y - A.y * B.x <= 0)
return 0;
return 1;
}
void solve()
{
memset(tong, 0, sizeof tong);
memset(ans, 0, sizeof ans);
scanf("%d %d %d %d %d", &m, &sx, &sy, &ex, &ey);
for (int i = 1; i <= n; i++)
scanf("%d %d", &s[i].u, &s[i].d);
sort(s + 1, s + 1 + n);
s[n + 1].u = s[n + 1].d = ex;
for (int i = 1; i <= m; i++)
{
int x, y;
scanf("%d %d", &x, &y);
for (int j = 1; j <= n + 1; j++)
{
Vector A, B, C, D;
A.x = s[j - 1].u - x;
A.y = sy - y;
B.x = s[j - 1].d - x;
B.y = ey - y;
C.x = s[j].u - x;
C.y = sy - y;
D.x = s[j].d - x;
D.y = ey - y;
if (check(A, B) && !check(C, D))
{
tong[j]++;
break;
}
}
}
for (int i = 1; i <= n + 1; i++)
{
if (tong[i])
ans[tong[i]]++;
}
printf("Box\\n");
for (int i = 1; i <= n + 1; i++)
if (ans[i])
printf("%d: %d\\n", i, ans[i]);
}
int main()
{
while (scanf("%d", &n) && n)
solve();
return 0;
}
以上是关于POJ2398计算几何叉积判断点在线段左/右侧的主要内容,如果未能解决你的问题,请参考以下文章