8.剑指Offer --- 英文版新增面试题

Posted 2021-10-21 enlyhua

第8章 英文版新增面试题

8.1 数组

面试题51：数组中重复的数字
	题目：在一个长度为n的数组里的所有数字都在0到n-1的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出
数组中任意一个重复的数字。例如，输入长度为7的数组{2,3,1,0,2,5,3}，那么对应的输出是重复数字的2或者3.
	
	解法一：先把输入的数组排序，从排序的数组中找出重复的数字。排序长度为n的数组需要 O(nlogn)的时间。

	解法二：还可以利用哈希表来解决。

	解法三：现在让我们重排这个数组。从头到尾依次扫描这个数组中的每个数字。当扫描到下标为i的数字时，首先比较这个数字(用m表示)是不是等于i。如果是，
接着扫描下一个数字。如果不是，再拿它和第m个数字进行比较。如果它和第m个数字相等，就找到了一个重复的数字(该数字在下标为i和m的位置都出现了)。如果它和
第m个数字不相等，就把第i个数字和第m个数字交换，把m放到属于它的位置。接下来重复这个比较，交换的过程，直到我们发现一个重复的数字。
	
	以数组 {2,3,1,0,2,5,3} 为例。数组的第0个数字是2，与它的下标不相等，于是把它和下标为2的数字1交换。交换后的数组是{1,3,2,0,2,5,3}。此时第0个
数字是1，仍然与它的下标不相等，继续把它和下标为1的数字3交换，得到数组{3,1,2,0,2,5,3}。接下来继续交换第0个数字3和第3个数字0，得到数组
{0,1,2,3,2,5,3}。此时第0个数值为0，接着扫描下一个数字。接下来的几个数字中，下标为1，2，3的三个数字分别为1，2，3，它们的下标和数值都相等，因此不需要
任何操作。接下来扫描到下标为4的数字2，由于它的数值和下标不相等，再比较它和下标为2的数字，注意到此时数组中下标为2的数字也是2，也就是数字2在下标2和下标
4的两个位置都出现了，因此找到一个重复的数字。

bool duplicate(int numbers[], int length, int* duplication)
{
	if (numbers == null || length <= 0)
		return false;

	for (int i = 0; i < length; i++) {
		if(numbers[i] < 0 || numbers[i] > length - 1) {
			return false;
		}
	}

	for (int i = 0; i < length; i++) {
		while (numbers[i] != i) {
			if (numbers[i] == numbers[numbers[i]]) {
				*duplication = numbers[i];
				return true;
			}

			//交换 numbers[i] 和 numbers[numbers[i]]
			int temp = numbers[i];
			numbers[i] = numbers[temp];
			numbers[temp] = temp;
		}
	}

	return false
}
	尽管代码中有两层循环，但每个数字最多只要交换两次就能找到属于它自己的位置，因此总的时间复杂度是O(n)。所有操作都是在输入数组上进行的，
空间复杂度为O(1)。


面试题52：构建乘积数组
	题目：给定一个数组 A[0,1,...,n-1]，请构建一个数组B[0,1,...,n-1]，其中B中的元素B[i]=A[0]*A[1],...,*A[i+1],...,*A[n-1]。
不能使用除法。
	
void multiply(const vector<double>& array1, vector<double>& array2)
{
	int length1 = array1.size();
	int length2 = array2.size();

	if (length1 == length2 && length2 > 1) {
		array2[0] = 1;
		for (int i = 1; i < length1; i++) {
			array2[i] = array2[i - 1] * array1[i -1];
		}

		double temp = 1;
		for (int i = length1 - 2; i >= 0; i++) {
			temp *= array1[i+1];
			array2[i] = temp;
		}
	}
}	
	
	时间复杂度是O(n)。


8.2 字符串
	题目：请实现一个函数用来匹配包含 "." 和 "*"的正则表达式。模式中的字符"."表示任意一个字符，而"*"表示它前面的字符可以出现任意次(包含0次)。
在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串'aaa' 与模式 'a.a' 和 'ab*ac*a'匹配，但与 'aa.a' 及 'ab*a'均不匹配。
	

bool match(char* str, cahr* pattern)
{
	if (str == null || pattern == null)
		return false;

	return matchCore(str, pattern);
}	

bool matchCore(char* str, char* pattern)
{
	if (*str == '\\0' ** *pattern == '\\0') 
		return true;

	if (*str != '\\0' && *pattern == '\\0') 
		return false;

	if (*(pattern + 1) == '*') {
		if (*pattern == *str || (*pattern == '.' && *str != '\\0')) {
			return matchCore(str + 1, pattern + 2) || matchCore(str + 1, pattern) || matchCore(str, pattern + 2);
		} else {
			return matchCore(str, pattern + 2);
		}
	}

	if (*str == *pattern || (*pattern == '.' && *str != '\\0')) {
		return matchCore(str + 1, pattern + 1);
	}

	return false;
}


面试题54：表示数值的字符串
	题目：请实现一个函数来判断字符串是否表示数值(包括整数和小数)。例如，字符串"+100"，"5e2"，"-123"，"3.1416"，及 "-1E-16" 都表示数值，
但 "12e"，"1a3.14"，"1.2.3"，"+-5"及"12e+5.4"都不是。
	
	表示数值的字符串遵循下面的模式：
[sign] integral-digits [. [fractional-digits] ] [ e|E [sign]exponential-digits]
	
	a) 数值前面可能有一个表示正负的'-'或者'+'；
	b) 接下来是若干个0~9的数位表示数值的整数部分(在某些小数里可能没有数值的整数部分)；
	c) 如果是小数，那么在小数点后面可能会有若干个0~9的数位表示小数部分；
	d) 如果用科学计数法表示，接下来是一个'e'或者'E'，以及紧跟着的一个整数(可以有正负)表示指数。

bool isNumberice(char* string)
{
	if (string == null)
		return false;

	if (*string == '+' || *string == '-') 
		++string;

	if (*string == '\\0')
		return false;

	bool numeric = true;

	scanDigits(&string);
	if (*string != '\\0') {
		if (*string == '.') {
			++string;
			scanDigits(&string);

			if (*string == 'e' || *string == 'E') 
				numeric = isExponential(&string);
		} else if (*string == 'e' || *string == 'E') {
			numeric = isExponential(&string);
		} else {
			numeric = false;
		}
	}

	return numeric && *string =- '\\0';
}

//用来扫描字符串中0到9的数字
void scanDigits(char** string)
{
	while (**string != '\\0' && **string >= '0' && **string <= '9') {
		++(**string);
	}
}

//用来匹配科学记数法表示的数值的结尾部分。结尾部分的第一个字符是 'e' 或者 'E'，接下来可能有一个正负号，再紧跟着是若干0到9的数位。
bool isExponential(char** string)
{
	if (**string != 'e' && **string != 'E') {
		return false;
	}

	++(**string);

	if (**string == '+' || **string == '-') {
		++(**string);
	}

	if (**string == \\0) {
		return false;
	}

	scanDigits(string);

	return (**string == \\0) ? true : false;
}


面试题55：字符流中第一个不重复的字符
	题目：请实现一个函数用来找出字符流中第一个只出现一次的字符。例如，当从字符流中只读出前两个字符'go'时，第一个只出现一次的字符是'g'。当从
该字符流中读出前六字符'google'时，第一个只出现一次的字符是'l'。


class CharStatistics
{
	public:
		CharStatistics(): index(0)
		{	
			//初始化为-1
			for (int i = 0; i < 256; i++) {
				occurrence[i] = -1;
			}
		}

		void Insert(char ch)
		{
			if (occurrence[ch] == -1) {
				occurrence[ch] = index;

				//再次读到，更新为-2
			} else if (occurrence[ch] >= 0) {
				occurrence[ch] = -2;
			} 

			index++;
		}

		//当我们需要找到目前为止从字符流里读出的所有字符中的第一个不重复的字符时，我们只需要扫描整个数组，并从中找出最小的大于等于0的值对应的字符。
		char FirstAppearingOnce()
		{
			char ch = '\\0';
			int minIndex = numeric_limites<int>::max();

			for (int i = 0; i < 256; i++) {
				if (occurrence[i] >= 0 && occurrence[i] < minIndex) {
					ch = (char)i;
					minIndex = occurrence[i];
				}

				return ch;
			}
		}

	private:
		int occurrence[256];
		int index;
};


8.3 链表

面试题56：链表中环的入口节点
	题目：一个链表中有环，如何找出环的入口结点？例如，在图8.3的链表中，环的入口结点是结点3.

	分析：
		先定义两个指针p1和p2指向链表的头结点。如果链表中的环有n个结点，指针p1先在链表上向前移动n步，然后两个指针以相同的速度向前移动。当第二个指针
	指向环的入口结点时，第一个指针以及围绕着环走了一圈回到了入口结点。

		在有环的链表中找到环的入口结点的步骤：
			1.指针p1和p2在初始化时都指向链表的头结点；
			2.由于环中有4个节点，指针p1先在链表上先前移动4步；
			3.指针p1和p2以相同的速度在链表上移动，直到它们相遇。它们相遇的结点就是环的入口。

		剩下的问题就是如何得到环中结点的数目：
			可以用一块一慢指针。如果两个指针相遇，表明链表中存在环。两个指针相遇的结点一定是在环中。可以从这个结点出发，一遍继续向前移动一边计数，
		当再次回到这个结点的时候，就可以得到环中结点数了。

//在链表中有环的情况下找到一快一慢两个指针相遇的结点。如果不存在环，那么返回null
ListNode* MeetingNode(ListNode* pHead)
{
	if (pHead == null) {
		return null;
	}

	ListNode* pSlow = pHead->m_pNext;
	if (pSlow == null) {
		return null;
	}

	ListNode* pFast = pSlow->m_pNext;
	while (pFast != null && pSlow != null) {
		if (pFast == pSlow) {
			return pFast;
		}

		pSlow = pSlow->m_pNext;

		pFast = pFast->m_pNext;
		if (pFast != null) {
			pFast = pFast->m_pNext;
		}
	}

	return null;
}

//找到环中任意一个结点之后，就能得出环中的结点数目，并找到环的入口结点。
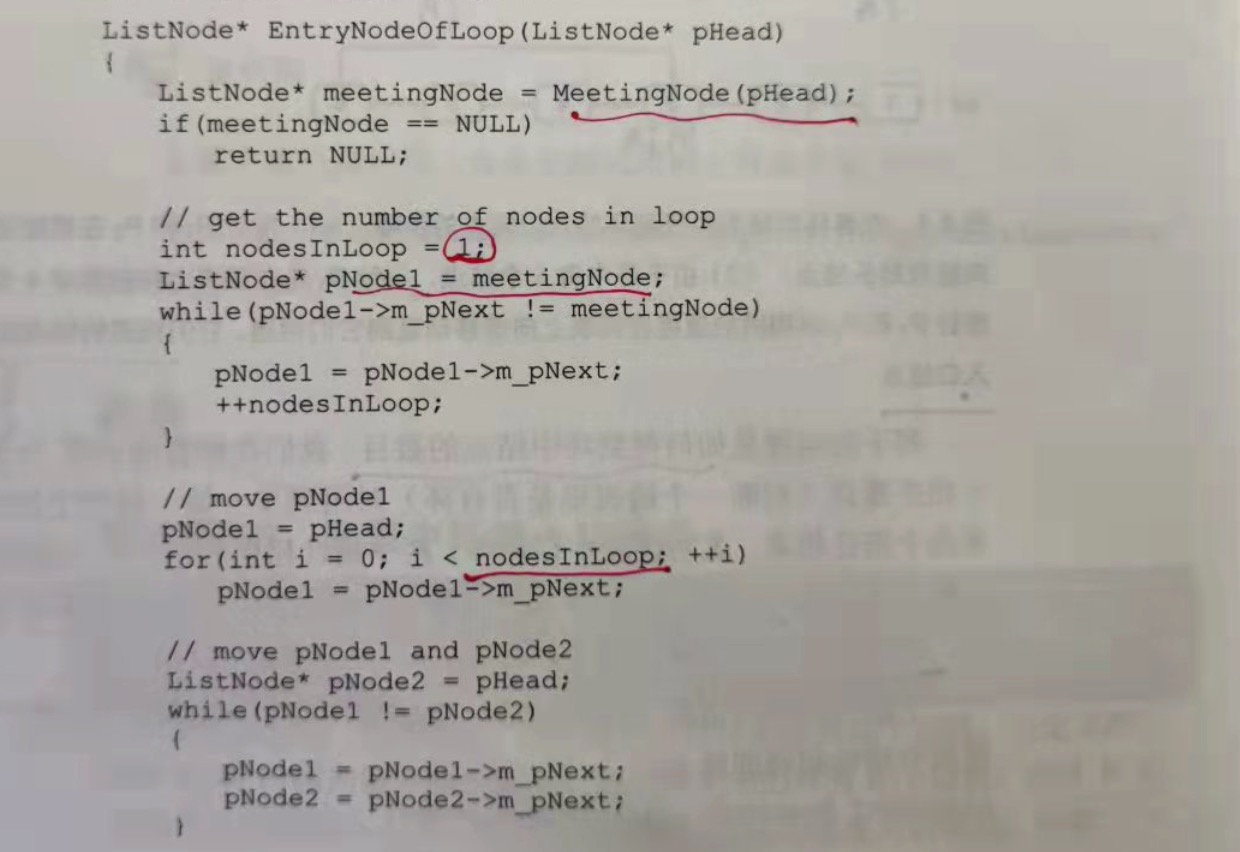
ListNode* EntryNodeOfLoop(ListNode* pHead)
{
	ListNode* meetingNode = MeetingNode(pHead);
	if (meetingNode == null) 
		return null;

	//计算环中的结点数
	int nodesInLoop = 1;
	ListNode* pNode1 = meetingNode;
	while (pNode->m_pNext != meetingNode) {
		pNode1 = pNode1->m_pNext;
		nodesInLoop++;
	}

	//pNode1 先移动 n 步
	pNode1 = pHead;
	for (int i = 0; i < nodesInLoop; i++) {
		pNode1 = pNode1->m_pNext;
	}

	//找p1和p2相遇的点
	ListNode* pNode2 = pHead;
	while (pNode1 != pNode2) {
		pNode1 = pNode1->m_pNext;
		pNode2 = pNode2->m_pNext;
	}

	return pNode1;
}


面试题57：删除链表中重复的结点
	题目：在一个排序的链表中，如何删除重复的结点？
	1 -> 2 -> 3 -> 3 -> 4 -> 4 -> 5
删除重复结点后：
	1 -> 2 -> 5

	分析：
		第一步是要确定被删除的参数，头结点也有可能与后面的结点重复，也就是说头结点也可能被删除。因此删除函数应该声明为 
	void deleteDuplication(ListNode** pHead)，而不是 void deleteDuplication(ListNode* pHead)。

		接下来我们遍历整个链表。如果当前结点(代码中的pNode)的值与下一个结点的值相同，那么它就是重复的结点，都可以被删除。为了保证删除之后的链表
	仍然是相连的没有断开，我们要把当前结点的前一个结点(代码中的pPreNode)和后面比当前结点的值要大的结点相连。我们要确保pPreNode要始终与下一个没有
	重复的结点相连在一起。

void deleteDuplication(ListNode** pHead)
{
	if (pHead == null || *pHead == null)
		return;

	ListNode* pPreNode = null;
	ListNode* pNode = *pHead;

	while (pNode != null) {
		ListNode* pNext = pNode->m_pNext;
		bool needDelete = false;

		if (pNext != null && pNext->m_nValue == pNode->m_nValue) 
			needDelete = true;

		if (!needDelete) {
			pPreNode = pNode;
			pNode = pNode->m_pNext;
		} else {
			int value = pNode->m_nValue;
			ListNode* pToBeDel = pNode;

			while (pToBeDel != null && pToBeDel->m_nValue == value) {
				pNext = pToBeDel->m_pNext;
				delete pToBeDel;
				pToBeDel = null;
				pToBeDel = pNext;
			}

			if (pPreNode == null) {
				*pHead = pNext;
			} esle {
				pPreNode->m_pNext = pNext;
			}

			pNode = pNext;
		}
	}
}


8.4 树
面试题58：二叉树的下一个结点
	题目：给定一颗二叉树和其中的一个结点，如何找出中序遍历顺序的下一个结点？树中的结点除了有两个分别指向左右子结点的指针以外，还有一个指向父结点的指针。

BinaryTreeNode* GetNext(BinaryTreeNode* pNode)
{
	if (pNode == null)
		return null;

	BinaryTreeNode* pNext = null;
	if (pNode->m_pRight != null) {
		BinaryTreeNode* pRight = pNode->m_pRight;
		while (pRight->m_pLeft != null) {
			pRight = pRight->m_pLeft;
		}

		pNext = pRight;
	} else if (pNode->m_pParent != null) {
		BinaryTreeNode* pCurrent = pNode;
		BinaryTreeNode* pParent = pNode->m_pParent;
		while (pParent != null && pCurrent == pParent->m_pRight) {
			pCurrent = pParent;
			pParent = pParent->m_pParent;
		}

		pNext = pParent;
	}

	return pNext;
}


面试题59：对称的二叉树
	题目：请实现一个函数，用来判断一颗二叉树是不是对称的。如果一颗二叉树和它的镜像是一样的，那么它是对称的。

bool isSymmetrical(BinaryTreeNode* pRoot)
{
	return isSymmetrical(pRoot, pRoot);
}

bool isSymmetrical(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{
	if (pRoot1 == null && pRoot2 == null)
		return true;

	if (pRoot1 == null || pRoot2 == null)
		return false;

	if (pRoot1->m_nValue != pRoot2->m_nValue) 
		return false;

	return isSymmetrical(pRoot1->m_pLeft, pRoot2->m_pRight) && isSymmetrical(pRoot1->m_pRight, pRoot2->m_pLeft);
}


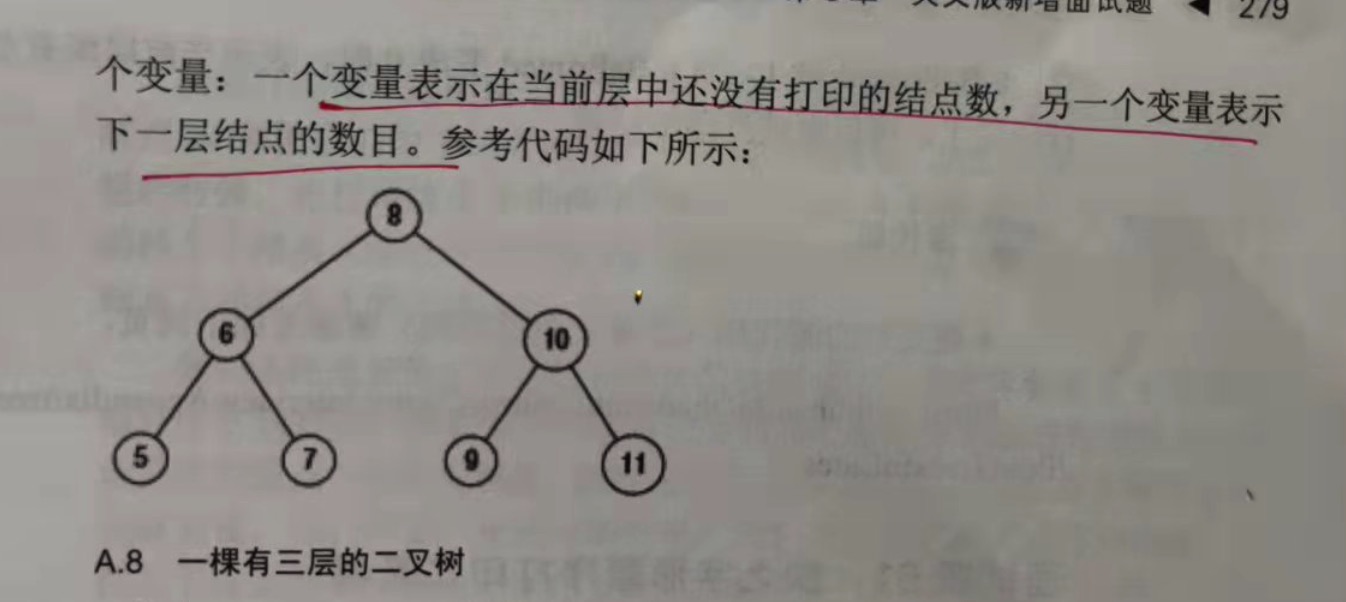
面试题60：把二叉树打印成多行
	题目：从上到下按层打印二叉树，同一层的结点按照从左到右的顺序打印，每一层打印到一行。

	分析：
		用一个队列来保存将要打印的结点。我们需要2个变量：一个变量表示在当前层中还没有打印的结点数，另外一个变量表示下一层结点的数目。

void Print(BinaryTreeNode* pRoot)
{
	if (pRoot == null)
		return ;

	std::queue<BinaryTreeNode*> nodes;
	nodes.push(pRoot);

	//下一层的结点数
	int nextLevel = 0;
	//当层中还没有打印的结点
	int toBePrinted = 1;

	while (!nodes.empty()) {
		BinaryTreeNode* pNode = nodes.front();
		printf("%d ", pNode->m_nValue);

		//把子节点加入到队列中
		if (pNode->m_pLeft != null) {
			nodes.push(pNode->m_pLeft);
			++nextLevel;
		}

		if (pNode->m_pRight != null) {
			nodes.push(pNode->m_pRight);
			++nextLevel;
		}

		nodes.pop();
		--toBePrinted;

		if (toBePrinted == 0) {
			printf("\\n");
			toBePrinted = nextLevel;
			nextLevel = 0;
		}
	}
}
	
	在上述代码中，变量 toBePrinted 表示在当前层中还没有打印的结点数，而变量 nextLevel 表示下一层的结点数。如果一个结点有子节点，我们把一个
子节点加入到队列中，同时把变量 nextLevel 加1。每当我们打印一个结点，toBePrinted 减1.当 toBePrinted 变成0时，表示当前层所有结点已经打印完了，
可以继续打印下一层。


面试题61：按之自行顺序打印二叉树
	题目：请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右往左的顺序打印，第三行再按照从左到右的顺序打印，其他行
以此类推。
	
	分析：
		按之字形打印二叉树需要两个栈。我们在打印某一行结点的时候，把下一层的子结点保存到相应的栈里。如果当前打印的是奇数层，则先保存左子节点再保存
	右子结点到第一个栈里；如果打印的是偶数层，则先保存右子结点再保存左子节点到第二个栈里。

void Print(BinaryTreeNode* pRoot)
{
	if (pRoot == null)
		return;

	std::stack<BinaryTreeNode*> levels[2];
	int current = 0;
	int next = 1;

	levels[current].push(pRoot);

	while (!levels[0].empty() || !levels[1].empty()) {
		BinaryTreeNode* pNode = levels[current].top();
		levels[current].pop();

		printf("%d ", pNode->m_nValue);

		if (current == 0) {
			if (pRoot->m_pLeft != null) {
				levels[next].push(pNode->m_pLeft);
			}

			if (pNode->m_pRight != null) {
				levels[next].push(pNode->m_pRight);
			}
		} else {
			if (pNode->m_pRight != null) {
				levels[next].push(pNode->m_pRight);
			}

			if (pNode->m_pLeft != null) {
				levels[next].push(pNode->m_pLeft);
			}
		}

		if (levels[current].empty()) {
			printf("\\n");
			current = 1 - current;
			next = 1 - next;
		}
	}
}
	
	上述代码定义了两个栈levels[0]和levels[1]。当打印一个栈里的结点时，它的子节点保存到另外一个栈中。当一层所有的节点都打印完了，交换这两个栈并
继续打印下一层。


面试题62：序列化二叉树
	题目：请实现两个函数，分别用来序列化和反序列化二叉树。

//这个二叉树序列化的算法
void Serialize(BinaryTreeNode* pRoot, ostream& stream)
{
	if (pRoot == null) {
		stream << "$,";
		return;
	}

	stream << pRoot->m_nValue << ',';
	Serialize(pRoot->m_pLeft, stream);
	Serialize(pRoot->m_pRight, stream);
}

void Deserialize(BinaryTreeNode** pRoot, istream& stream)
{
	int number;

	if (ReadStream(stream, &number)) {
		*pRoot = new BinaryTreeNode();
		(*pRoot)->m_nValue = number;
		(*pRoot)->m_pLeft = null;
		(*pRoot)->m_pRight = null;

		Deserialize(&((*pRoot)->m_pLeft), stream);
		Deserialize(&((*pRoot)->m_pRight), stream);
	}
}


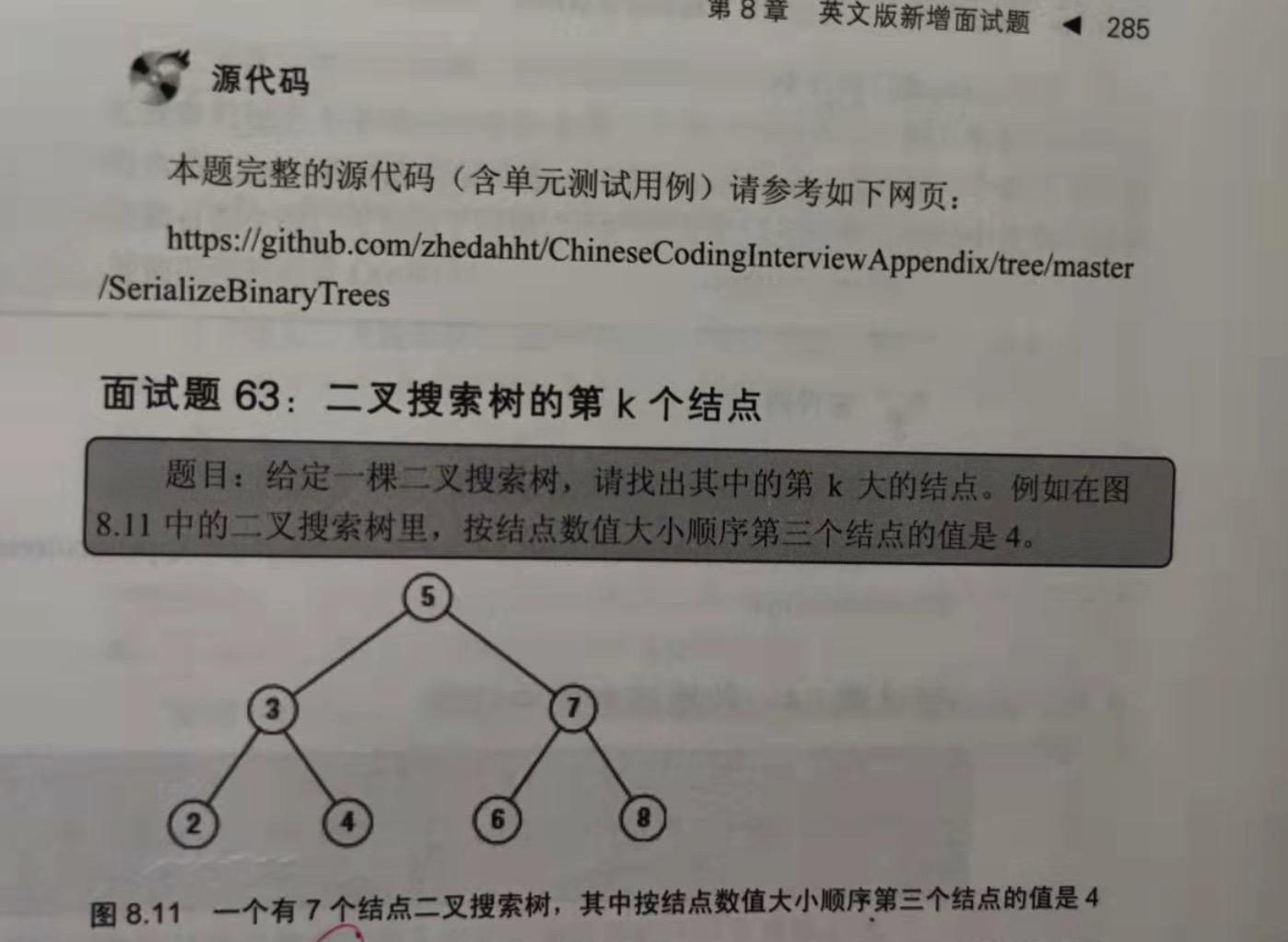
面试题63：二叉搜索树的第k个结点
	题目：给定一颗二叉搜索树，请找出其中的第k大的结点。

	分析：
		只要用中序遍历一颗二叉搜索树，就很容易找出它的第k大结点。

BinaryTreeNode* KthNode(BinaryTreeNode* pRoot, unsigned int k)
{
	if (pRoot == null || k == 0)
		return null;

	return KthNodeCore(pRoot, k);
}

BinaryTreeNode* KthNodeCore(BinaryTreeNode* pRoot, unsigned int& k)
{
	BinaryTreeNode* target = null;

	if (pRoot->m_pLeft != null) {
		target = KthNodeCore(pRoot->m_pLeft, k);
	}

	if (target == null) {
		if (k == 1) {
			target = pRoot;
		}

		k--;
	}

	if (target == null && pRoot->m_pRight != null) {
		target = KthNodeCore(pRoot->m_pRight, k);
	}

	return target;
}


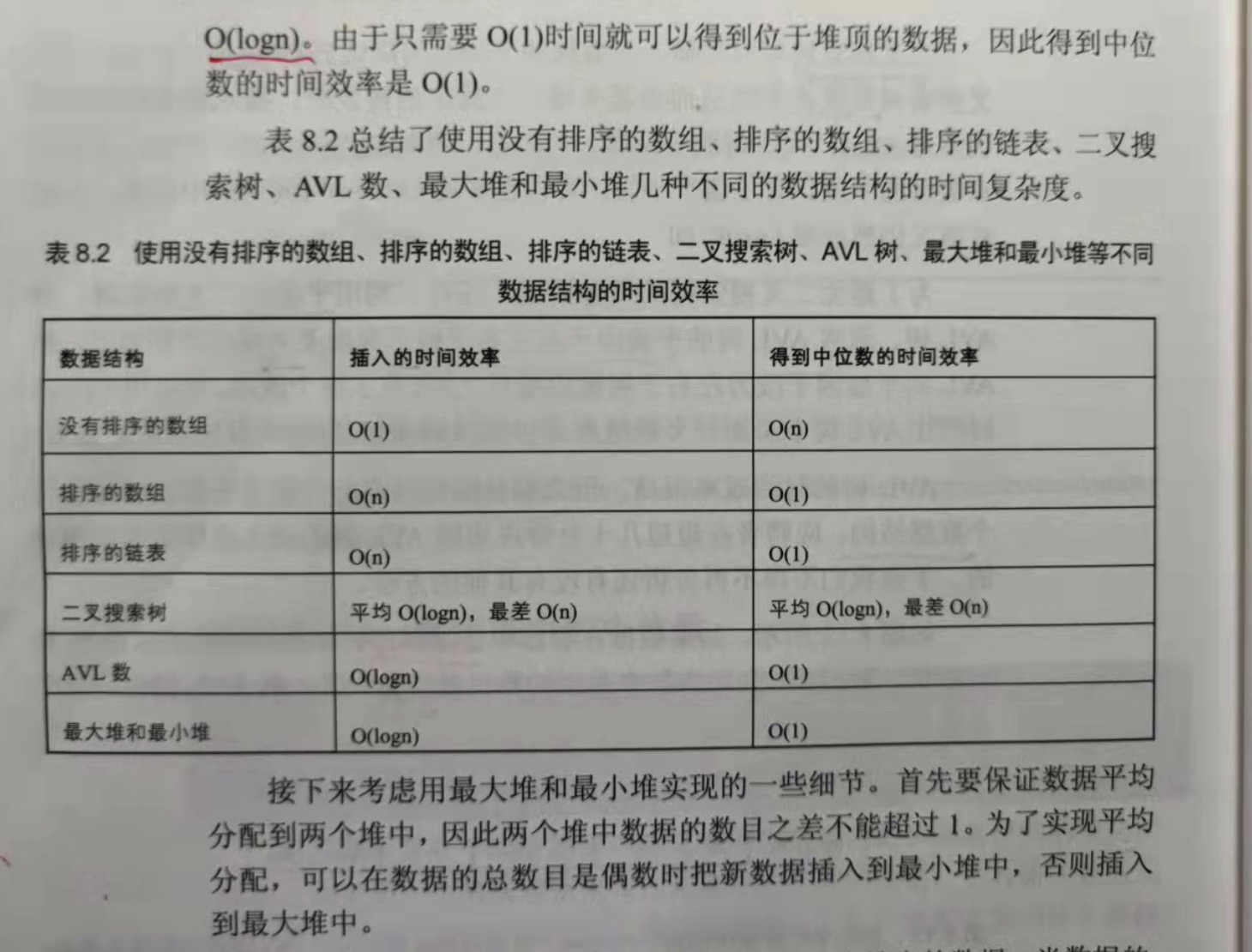
面试题64：数据流总的中位数
	题目：如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，
那么中位数就是所有数值排序之后中间两个数的平均值。
	

template<typename T> class DynamicArray
{
	public:
		void Insert(T num)
		{
			if ( ( (min.size() + max.size()) & 1 ) == 0 ) {
				if (max.size() > 0 && num < max[0]) {
					max.push_back(num);
					push_heap(max.begin(), max.end(), less<T>());

					num = max[0];

					pop_heap(max.begin(), max.end(), less<T>());
					max.pop_back();
				}

				min.push_back(num);
				push_heap(min.begin(), min.end(), gtreater<T>()));
			} else {
				if (min.size() > 0 && min[0] < num) {
					min.push_back(num);
					push_heap(min.begin(), min.end(), greater<T>());

					num = min[0];

					pop_heap(min.begin(), min.end(), greater<T>());
					min.pop_back();
				}

				max.push_back(num);
				push_heap(max.begin(), max.end(), less<T>());
			}
		}

		T GetMedian()
		{
			int size = min.size() + max.size();
			if (size == 0) {
				throw exception("No numbers are available");
			}

			T median = 0;
			if ( (size & 1) == 1 ) {
				median = min[0];
			} else {
				median = (min[0] + max[0]) / 2;
			}

			return median;
		}

	private:
		vector<T> min;
		vector<T> max;
};


8.5 栈和队列

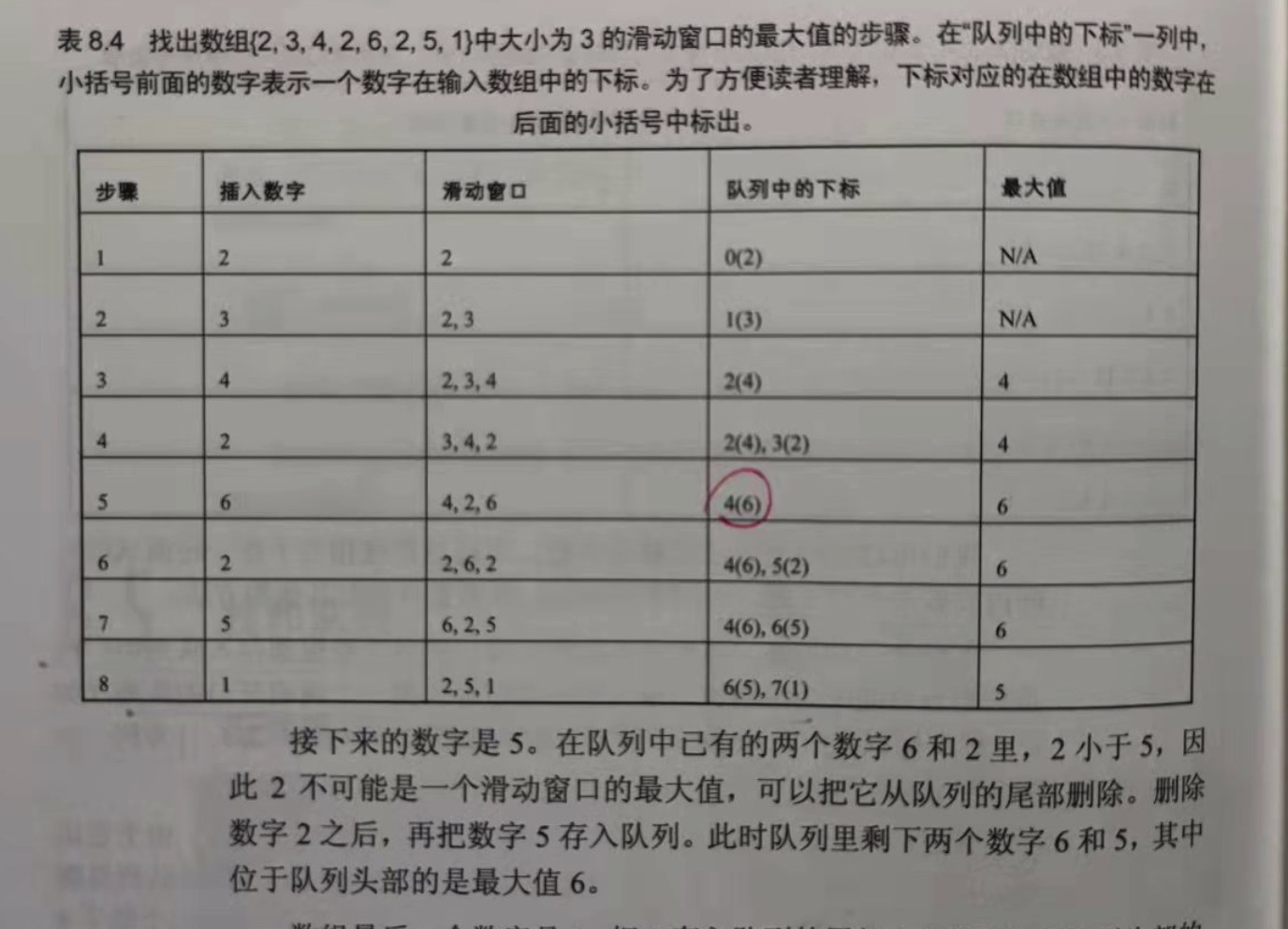
面试题65：滑动窗口的最大值
	题目：给定一个数组和滑动窗口的大小，请找出所有滑动窗口里的最大值。例如，如果输入数组 {2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个
滑动窗口，它们的最大值分别为{4,4,6,6,6,5}。
	
	分析：
		实际上一个滑动窗口可以看成一个队列。当滑动窗口滑动时，处于窗口的第一个数字被删除，同时在窗口的末尾添加一个新的数字。这符合队列的先进先出
	的特性。如果能从队列中找出它的最大数，这个问题也解决了。

vector<int> maxInWindows(const vector<int>& num, unsigned int sieze)
{
	vector<int> maxInWindows;
	if (num.size() >= size && size >= 1) {
		//index双端队列
		deque<int> index;

		for (unsigned int i = 0; i < size; i++) {
			while (!index.empty() && num[i] >= num[index.back()]) {
				index.pop_back();
			}

			index.push_back(i);
		}

		for (unsigned int i = size; i < num.size(); i++) {
			maxInWindows.push_back(num[index.front()]);

			while (!index.empty() && num[i] >= num[index.back()]) {
				index.pop_back();
			}

			if (!index.empty() && index.front() <= (int)(i - size)) {
				index.pop_front();
			}

			index.push_back(i);
		}

		maxInWindows.push_back(num[index.front()]);
	}

	return maxInWindows;
}
	
	上述代码中，index 是一个两端开口的队列，用来保存有可能是滑动窗口最大值的数字的下标。在存入一个数字的下标之前，首先要判断队列已有数字是否小于
待存入的数字。如果已有的数字小于待存入的数字，这些数字已经不可能是滑动窗口的最大值，因此它们将会依次从队列的尾部删除(调用函数 pop_back)。同时，
如果队列头部的数字已经从窗口里滑出，滑出的数字也需要从队列的头部删除(调用函数 pop_front)。由于队列的头部和尾部都有可能删除数字，这也是需要两端
开口队列的原因。


8.6 回溯法

面试题66：矩阵中的路径
	题目：请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中任意一格开始，每一步可以在矩阵中左，右，上，
下移动一个。如果一条路径经过了矩阵的某一格，那么该路径不能再次进入该格子。如下3*4的矩阵中包含一条字符串"bcced"的路径。但矩阵中不包含字符串"abcb"
的路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子后，路径不能再次进入这个格子了。

a b c e
s f c s
a d e e
	
	分析：
		这是一个可以用回溯法解决的典型题。由于回溯法的递归特性，路径可以被看成一个栈。

bool hasPath(char* matrix, int rows, int cols, char* str)
{
	if (matrix == null || rows < 1 || cols < 1 || str == null)
		return false;

	bool *visited = new bool[rows * cols];
	memset(visited, 0, rows * cols);

	int pathLength = 0;
	for (int row = 0; row < rows; row++) {
		for (int col = 0; col < cols; col++) {
			if (hasPathCore(matrix, rows, cols, row, col, str, pathLength, visited)) 
				return true;
		}
	}

	delete[] visited;

	return false;
}

bool hasPathCore(cahr* matrix, int rows, int cols, int row, int col, char* str, int& pathLength, bool* visited)
{
	if (str[pathLength] == '\\0')
		return true;

	bool hasPath = false;

	if (row  >= 0 && row < rows && col >= 0 && col < cols && matrix[row * cols + col] == str[pathLength] && !visited[row * cols + col]) {
		pathLength++;
		visited[row * cols + col] = true;

		hasPath = hasPathCore(matrix, rows, cols, row, col - 1, str, pathLength, visited) || 
				hasPathCore(matrix, rows, cols, row - 1, col, str, pathLength, visited) ||
				hasPathCore(matrix, rows, cols, row, col + 1, str, pathLength, visited) ||
				hasPathCore(matrix, rows, cols, row + 1, col, str, pathLength, visited);

		if (!hasPath) {
			pathLength--;
			visited[row * cols + col] = false;
		} 
	}

	return hasPath;
}


面试题67：机器人的运动范围
	题目：地上有一个m行n列的方格。一个机器人从坐标(0,0)的格子开始移动，它每一次可以向左，右，上，下移动一格，但不能进入行坐标和列坐标的数位之和大于
k的格子。例如，当k为18时，机器人能够进入方格(35,37)，因为 3+5+3+7=18。但它不能进入方格(35,38)，因为3+5+3+8=19。请问该机器人能够达到多少个格子？
	
int movingCount(int threshold, int rows, int cols)
{
	bool* visited = new bool[rows * cols];
	for (int i = 0; i < rows * cols; i++) {
		visited[i] = false;
	}

	int count = movingCountCore(threshold, rows, cols, 0, 0, visited);

	delete[] visited;

	return count;
}

int movingCountCore(int threshold, int rows, int cols, int row, int col, bool* visited)
{
	int count = 0;

	if (check(threshold, rows, cols, row, col, visited)) {
		visited[row * cols + col] = true;

		count = 1 + movingCountCore(threshold, rows, cols, row - 1, col, visited) + 
			    movingCountCore(threshold, rows, cols, row, col - 1, visited) + 
			    movingCountCore(threshold, rows, cols, row + 1, col, visited) + 
			    movingCountCore(threshold, rows, cols, row, col + 1, visited);
	}

	return count;
}

//check 判断机器人能否进入坐标为(row, col)的方格，而函数 getDigiSum 用来得到一个数字的数位之和。
bool check(int threshold, int rows, int cols, int row, int col, bool* visited)
{
	if (row >= 0 && row < rows && col >= 0 && col < cols && getDigitSum(row) + getDigitSum(col) <= threshold && !visited[row * cols + col])
		return true;

	return false;
}

int getDigitSum(int numbers)
{
	int sum = 0;

	while (number > 0) {
		sum += number % 10;
		number /= 10;
	}

	return sum;
}