The math behind dynamics of TCP BBR

Posted 2021-10-21 dog250

引

BBR中有很多诸如1.25，0.75，0.89，0.77之类的魔数字，它们是调教出来的经验值呢，还是可以用数学推导发出来呢？

这些问题在结果导向的当今非常无聊，但也勉强仅图一乐吧。对我自己而言，除了兴趣还有一些执念。
我不相信背后没有数学解释的东西，一开始我看不上BBR，就是因为它没有数学模型，类似AIMD，response function那样优美的数学模型，没有Reno/CUBIC中 $t=\alpha \sqrt{\frac{\beta }{p}}$这样的公式。

后来经neal在内的BBR Development groups大佬们的指点，加入一些自己的思考，发现BBR的确没有统一的数学模型，但在零散的每个细节背后都有严谨的数学，这让人感到舒服且兴奋。国庆节的清早，就把这些写写。

Startup状态gain的确定

Startup状态的gain在历史上有两个值，分别为2.89和2.77，它们的差别在于：

• 从cwnd算出pacing rate，则为2.89，这也是原始的理想结论。
• 从pacing rate算出cwnd，则为2.77，这是更加合理的最新结论。
  关于该话题，引述2018年和neal在BBR邮件讨论组里的交流：
  
  下面挨个看。

2.77的推导
设$f(x)$和$g(x)$分别为BBR在Startup状态的pacing rate函数和cwnd函数，$P_{init}$和$W_{init}$分别为初始pacing rate和初始cwnd，根据慢启动原理：

$f(x)=P_{init}\times 2^x$
$g(x)=W_{init}\times 2^x$

计算简化起见，设$P_{init}=W_{init}=1$.
cwnd与BDP是等计量的，BDP显然是pacing rate在一个区间的积分：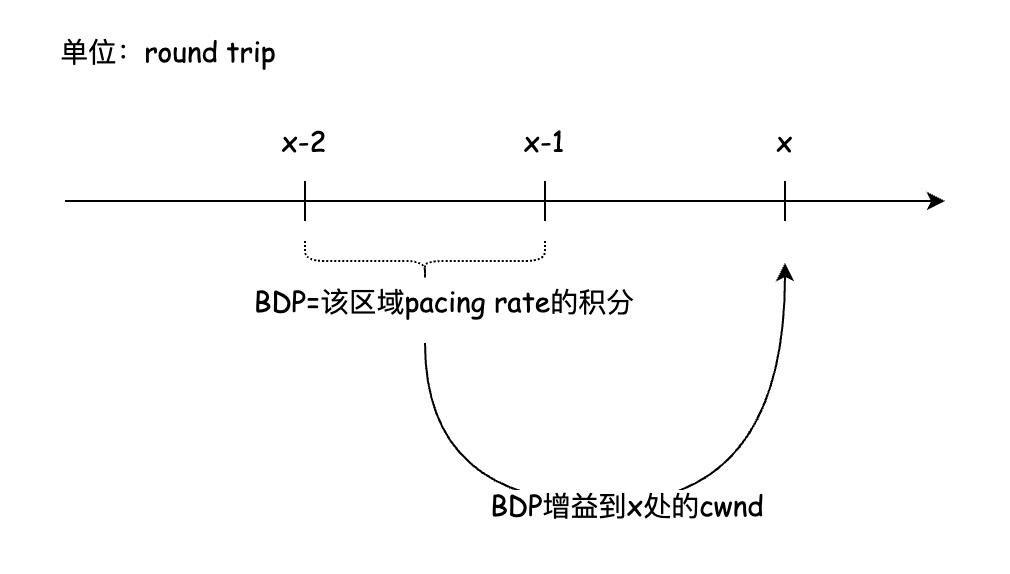
如上图，显然有：

$BD{P}_{x-2}^{x-1}={\int }_{x-2}^{x-1}f(x)={\int }_{x-2}^{x-1}{2}^{x}dx=\frac{2^x}{4\ln 2}$

根据cwnd函数，则有：

$W_x=g(x)=2^x$

若$W_x$是在$BD{P}_{x-2}^{x-1}$的基础上通过乘以一个gain而来，设gain为$g$，则：

$W_x=g\times BD{P}_{x-2}^{x-1}=g\times \frac{2^x}{4\ln 2}=2^x$

解出$g$：

$g=4\ln 2\approx 2.77$

2.89的推导
预设和2.77的推导一致，图示不一样：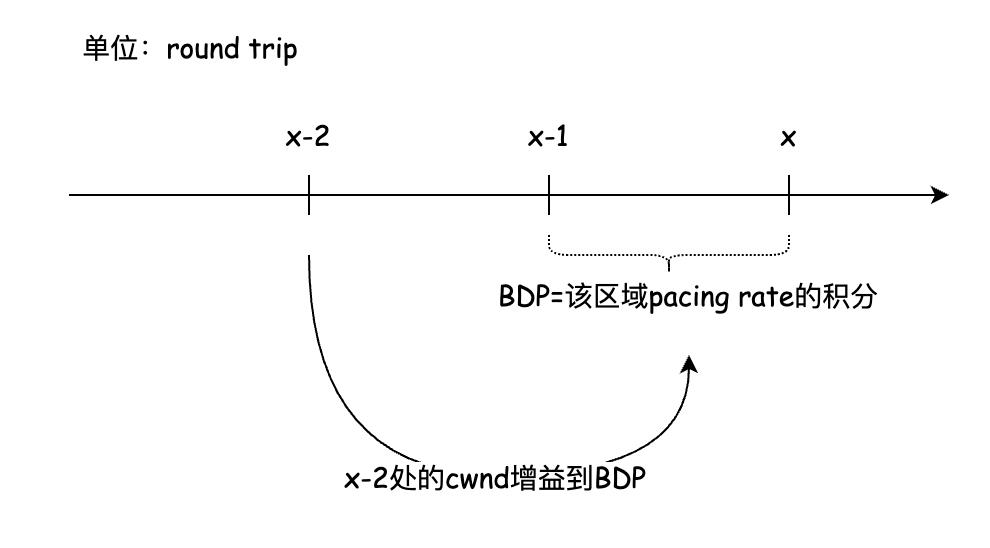

如上图，显然有：

$BD{P}_{x-1}^x={\int }_{x-1}^{x}f(x)dx=\frac{2^x}{2\ln 2}$

若$BD{P}_{x-1}^x$是在$W_{x-2}$的基础上通过乘以一个gain而来，设gain为$g$，则：

$BD{P}_{x-1}^x=\frac{2^x}{2\ln 2}=g\times g(x-2)=g\times \frac{2^x}{4}$

解出$g$：

$g=\frac{2}{\ln 2}\approx 2.89$

Drain状态gain的确定

详见下面“ProbeBW状态drain阶段的另一种可能(关于drain-to-target)”小节。

ProbeBW状态使用minRTT界定cycle phase的原因

当需要计时，有minRTT和packet-timed RTT可供使用，而BBR在ProbeBW状态采用了minRTT而不是packet-timed RTT，原因如下：

• probe同步问题
  感谢neal的解释：

  For what it’s worth, the motivation for using wall clock time rather than packet-timed round trips for triggering the end of a cycle phase was to avoid entrainment. We originally tried using packet-timed round trips, but noticed that this caused entrainment: flows aligned their phases based on the dynamics of the bottleneck queue; in turn this caused some flows to repeatedly probe for bandwidth at the same time as other flows, causing each flow in the synchronized ensemble to fail to realize that its fair share was higher. We found better bandwidth convergence by avoiding entrainment by explicitly randomizing the initial phase of the flows and then using wall clock time to trigger the progress through the bandwidth probing cycle.

  使用packet-timed RTT的问题在于会发生所谓的Entrainment，这将导致几个流同时进入probe阶段，之后又同时进行drain，从而破坏BBR在ProbeBW状态固有的公平收敛性。同步probe会让BBR造成误判，事实上并没有发生拥塞，只是大家一起probe导致的暂时假性拥塞。

  和简谐振动同步一样，probe同步也是有害的，详细解释为什么多个流会对齐它们的phase start时间不是本文的目的，只能直观上感受一下。

  多条流显然是在同一个buffer中相互作用的系统，它们之间的交互是probe同步的原因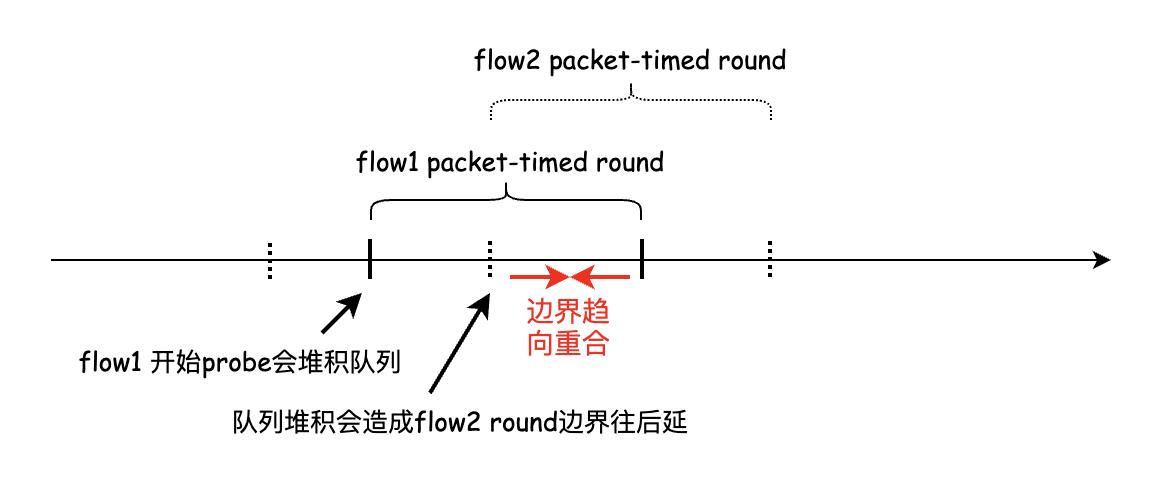：和荡秋千时为了让秋千快速停下来需要随机摇晃一样，随机化是破解同步的利器。我前段时间尝试以固定时间执行ProbeBW，也是有probe同步的风险的，解除这个风险有好几个方案：

  • 随机化每一个cycle phase的顺序。
  • 每一个cycle phase的时间在小时间范围随机化。
  • 小范围随机化cruise phase的数量。

  以上的随机方案可以叠加实施。

• 高丢包问题
  显然，packet-timed RTT大于等于minRTT的，使用更久的packet-timed RTT坚持probe可能会造成很高的丢包，比如在已经开始排队的系统中。下面是一个描述该场景的tcptrace图示：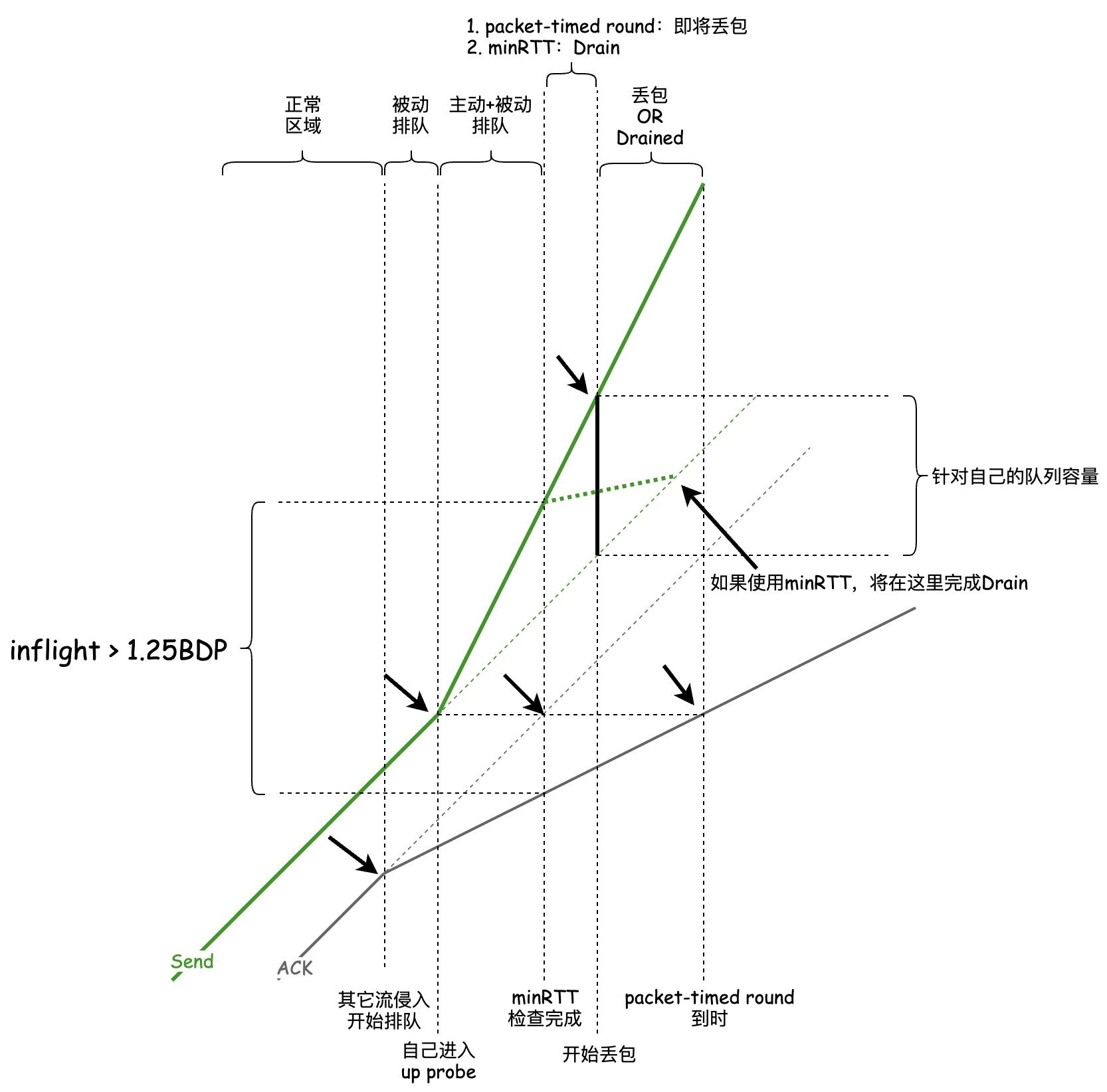
  凡事要分析两面性，纵然使用packet-timed round可能会出现probe同步以及高丢包，但它的好处是，packet-timed RTT可以天然识别排队。比如，通过packet-timed RTT和minRTT的比较，在识别出排队时，便可以跳过probe阶段了，因此此时的probe将会加剧拥塞。

  所以说，ProbeBW状态完全可以根据实际情况进行触发式自适应：

  • 触发式probe：在采集到minRTT或者RTT小到一定程度是马上进行probe。
  • 周期性probe：在时间段$T$内，至少保证要probe一次，以防饿死
  • probe和cruise阶段使用minRTT周期计数。
  • drain阶段使用packet-timed RTT周期计数(见最后一节)。

ProbeBW状态probe阶段BBR如何公平收敛

设一条流的带宽为$B$，probe增益为$g$，理想情况下，在probe之前和其它流完全共享整个带宽，设为1，带宽利用率为100%，则其它流的带宽为$1-B$.
当该流probe时，分两种情况：

• 有空余带宽加进来，该流理所当然获得 g × B g\\times B The magic behind array length property

  Discovering the Computer Science Behind Postgres Indexes

  Man's Best Friend: The Science Behind the Dog and Human Relationship

  The Architectural Principles Behind Vrbo’s GraphQL Implementation

  Analyzing The Papers Behind Facebook's Computer Vision Approach

  How Browsers Work: Behind the scenes of modern web browsers