C/C++ 编程中最常用的算法 - 穷举搜索

Posted 2021-10-21 cpp_learner

算法中，最常用的应该就是穷举搜索算法了吧，也许你已经使用过了，只是自己不知到而已！

---

讲述一道题目，你就会知道什么是穷举算法了！

我国古代数学家张丘建在《算经》一书中曾提出过著名的“百钱买百鸡”问题，该问题叙述如下：
鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一；百钱买百鸡，则翁、母、雏各几何？
上题的意思是公鸡一只五块钱，母鸡一只三块钱，小鸡三只一块钱，现在要用一百块钱买一百只鸡，问公鸡、母鸡、小鸡各多少只？

题目已经给出了，看着题目，你能想到的最简单的解决办法是什么？
是不是将全部结果都判断一次，然后超出符合条件的就可以了！

所以代码如下：

int main(void) {
	int fChook = 0;			// 公鸡数量
	int mChook = 0;			// 母鸡数量
	int litleChook = 0;		// 小鸡数量
	
	int count1 = 0;		// 统计循环次数

	for (fChook = 0; fChook <= 20; fChook++) {
		for (mChook = 0; mChook <= 33; mChook++) {
			for (litleChook = 3; litleChook <= 99; litleChook += 3) {
				count1++;
				if ((fChook * 5 + mChook * 3 + litleChook / 3) == 100 && (fChook + mChook + litleChook) == 100) {
					cout << "公鸡：" << fChook << "，母鸡：" << mChook << "，小鸡：" << litleChook << endl;
				}			
			}
		}
	}

	//cout << "未优化循环次数：" << count1 << endl;
	return 0;
}

为什么第一个for循环判断条件是小于等于20？
因为一只公鸡5元钱，5乘以20就刚好等于100元了，所以公鸡的数量不能超过20只。

为什么第二个for循环判断条件是小于等于33？
因为一只母鸡3元钱，3乘以33等于99元，所以母鸡的数量不能超过33只。

为什么第三个for循环判断条件是小于等于99？
小鸡三只1元钱，99除以3等于33元，且99只小鸡已经是顶峰了，因为不能单独买一只小鸡。

运行截图：

可以看到，不管怎么算都是正确的！

上面的代码，就是穷举搜索算法！

穷举法（枚举法）的基本思想是：

1. 列举出所有可能的情况，逐个判断有哪些是符合问题所要求的条件，从而得到问题的全部解答。
2. 它利用计算机运算速度快、精确度高的特点，对要解决问题的所有可能情况，一个不漏地进行检查，从中找出符合要求的答案。

用穷举算法解决问题，通常可以从两个方面进行分析：
（1）问题所涉及的情况：问题所涉及的情况有哪些，情况的种数必须可以确定。把它描述出来。应用穷举时对问题所涉及的有限种情形必须一一列举，既不能重复，也不能遗漏。重复列举直接引发增解，影响解的准确性；而列举的遗漏可能导致问题解的遗漏。
（2）答案需要满足的条件：分析出来的这些情况，需要满足什么条件，才成为问题的答案，把这些条件描述出来。

那他这样到底循环判定了多少次呢？还是上面那一套代码，将注释那行代码解开注释，再一次运行：

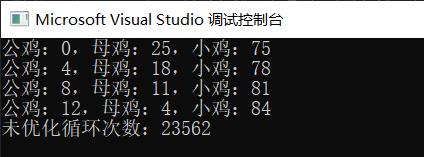
天呐！运行了两万多次，要不是我点的CUP还可以，这不得卡死？
不行，这代码绝对不行，我们来看看还有没有可以优化的地方！

这当然有！

就是当公鸡达到一定数量时，母鸡就无需判断那么多次了；当母鸡达到一定数量时，小鸡就无需判断那么多次了！
接着这个思路，我们来写优化代码。

优化后的代码如下：

int main(void) {
	int fChook = 0;			// 公鸡数量
	int mChook = 0;			// 母鸡数量
	int litleChook = 0;		// 小鸡数量

	int count1 = 0;
	int count2 = 0;

	for (fChook = 0; fChook <= 20; fChook++) {
		for (mChook = 0; mChook <= 33; mChook++) {
			for (litleChook = 3; litleChook <= 99; litleChook += 3) {
				count1++;
				if ((fChook * 5 + mChook * 3 + litleChook / 3) == 100 && (fChook + mChook + litleChook) == 100) {
					cout << "公鸡：" << fChook << "，母鸡：" << mChook << "，小鸡：" << litleChook << endl;
				}			
			}
		}
	}

	cout << endl << "-----------------华丽的分割线------------------" << endl << endl;

	/* 通过钱的总数控制 */
	for (fChook = 0; fChook <= 20; fChook++) {
		for (mChook = 0; mChook <= (100 - fChook * 5) / 3; mChook++) {
			for (litleChook = 3; litleChook <= (100 - (fChook * 5 + mChook * 3)) * 3; litleChook += 3) {
				count2++;
				if ((fChook * 5 + mChook * 3 + litleChook / 3) == 100 && (fChook + mChook + litleChook) == 100) {
					cout << "公鸡：" << fChook << "，母鸡：" << mChook << "，小鸡：" << litleChook << endl;
				}
			}
		}
	}

	cout << endl << "未优化循环次数：" << count1 << "，优化后循环次数：" << count2  << endl;

	return 0;
}

代码中，我是通过钱来控制剩下两个for循环的判断条件的。
第二个for循环，(100 - fChook * 5) / 3，先拿一百块钱减去当前公鸡数量所花费的钱，剩下的钱再除以一只母鸡的价格，那么就可以得到母鸡最多可以买多少只了。
第三个for循环也是一样的思路，一百元减去当前公鸡数量所花费的钱和母鸡数量所花费的钱，剩下来的钱，再乘以三(小鸡一只三元)，就可以得到小鸡还可以再买多少只了！

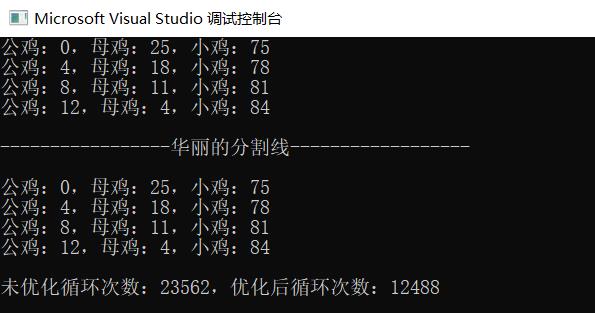
看到没有，优化后循环次数是一万两千多次，这效率瞬间提升了一半，这不得起飞？

当然，因该也还有其它的优化思路，这就得大家发动脑筋思考啦！

所以，大家懂了吧，即使是遍历全部结果，也还是有优化的空间的，这穷举算法也是不错的！（用最简单的办法，找出所需要的结果）

---

学会了这个用法，我们来做一道简单的练习题。

有 20 枚硬币，可能包括 4 种类型：1 元、5 角、1 角和 5 分。
已知 20 枚硬币的总价值为 10 元，求各种硬币的数量。

例如：4、11、5、0 就是一种方案。而 8、2、10、 0 是另一个可能的方案，显然方案并不是唯一的，请编写程序求出类似这样的不同的方案一共有多少种？
（1）编程思路。
直接对四种类型的硬币的个数进行穷举。其中，1 元最多 10 枚、5 角最多 20 枚、1 角最多 20 枚、5 分最多 20 枚。

开始写代码吧：
如果以元为单位，则 5 角、1 角、5 分会化成浮点型数据，容易计算出错。可以将 1元、5 角、1 角、5 分变成 100 分、50 分、10 分和 5 分，从而全部采用整型数据处理！

做法和思路跟上面类似，我就直接将代码列举出来了！

#include <iostream>
#include <string>

using namespace std;

int main(void) {
	int a100 = 0;	// 1元的硬币数量
	int a50 = 0;	// 5角的硬币数量
	int a10 = 0;	// 1角的硬币数量
	int a5 = 0;		// 5分的硬币数量
	int count = 0;	// 记录可行的方案总数

	int count1 = 0;
	int count3 = 0;

	for (a100 = 0; a100 <= 10; a100++) {
		for (a50 = 0; a50 <= 20; a50++) {
			for (a10 = 0; a10 <= 20; a10++) {
				for (a5 = 0; a5 <= 20; a5++) {
					count1++;
					if ((a100 * 100 + a50 * 50 + a10 * 10 + a5 * 5) == 1000 && (a100 + a50 + a10 + a5) == 20) {
						cout << "1元硬币：" << a100 << "枚， 5角硬币：" << a50 << "枚， 1角硬币：" << a10 << "枚， 5分硬币：" << a5 << "枚！" << endl;
						count++;
					}
				}// a5 end.
			}// a10 end.
		}// a50 end.
	}// a100 end.

	cout << "一共有：" << count << "种组合！" << endl;
	count = 0;


	cout << endl << "-----------------华丽的分割线------------------" << endl << endl;

	/* 通过硬币数量控制 */
	for (a100 = 0; a100 <= 10; a100++) {
		for (a50 = 0; a50 <= (20 - a100); a50++) {
			for (a10 = 0; a10 <= (20 - a100 - a50); a10++) {
				for (a5 = 0; a5 <= (20 - a100 - a50 - a10); a5++) {
					count3++;
					if ((a100 * 100 + a50 * 50 + a10 * 10 + a5 * 5) == 1000 && (a100 + a50 + a10 + a5) == 20) {
						cout << "1元硬币：" << a100 << "枚， 5角硬币：" << a50 << "枚， 1角硬币：" << a10 << "枚， 5分硬币：" << a5 << "枚！" << endl;
						count++;
					}
				}// a5 end.
			}// a10 end.
		}// a50 end.
	}// a100 end.


	cout << "一共有：" << count << "种组合！" << endl;

	cout << endl << "未优化循环次数：" << count1 << "，优化后循环次数：" << count3 << endl;

	return 0;
}

---

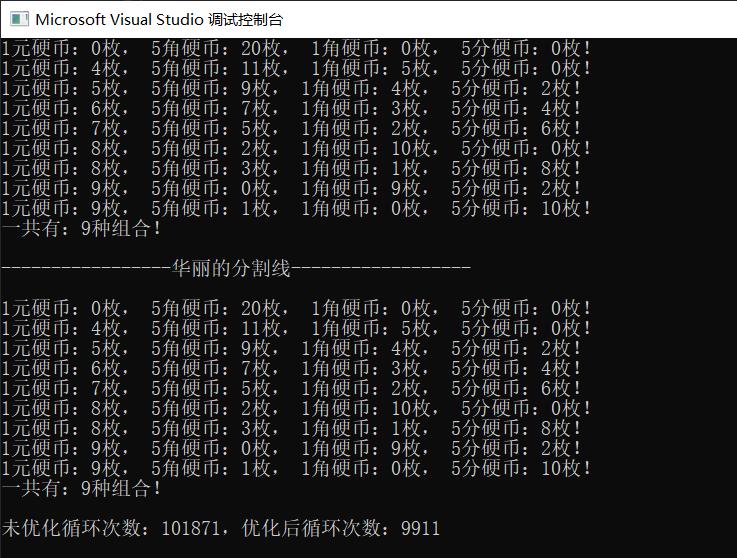
总结：

其实这个穷举搜索算法大家都会使用，重点是理解它的思路和过程；知道怎么去优化就可以的了！