原码反码补码&浮点类型的存储

Posted 2021-10-21 TangguTae

原码、反码、补码

原码就是人最直观的理解，对于有符号数，其最高位为符号位。例如对于8位有符号整数，[0000 1001]表示十进制下的7，而[1000 1001]表示的是十进制下的-7。

为什么要引入补码的概念呢？

计算机内存里面都是二进制的形式存储的，如果在计算机中如果用原码来表示一个数的话，在进行运算的时候还需要识别其符号位。在计算机中其实没有用来实现减法的逻辑门，它是通过加法来实现的。因为任何减法比如X - Y都可以表示为X + (-Y)。

为了方便计算机直接进行运算，引入补码。

例如-2+3=1；

-2的原码：1000 0010，补码1111 1110

3的原码： 0000 0011，补码0000 0011

如果用原码计算，逐位相加，得到的结果1000 0101，表示的是-5，所以是错的

采用补码的话，得到的补码结果是0000 0001，原码为0000 0001，值为1，是正确的结果。

补码 = 原码取反 （符号位不变）+ 1；

-2的补码：1000 0010取反得到1111 0010，然后+1, 得到补码1111 0011

正数的原码、反码、补码都是它本身

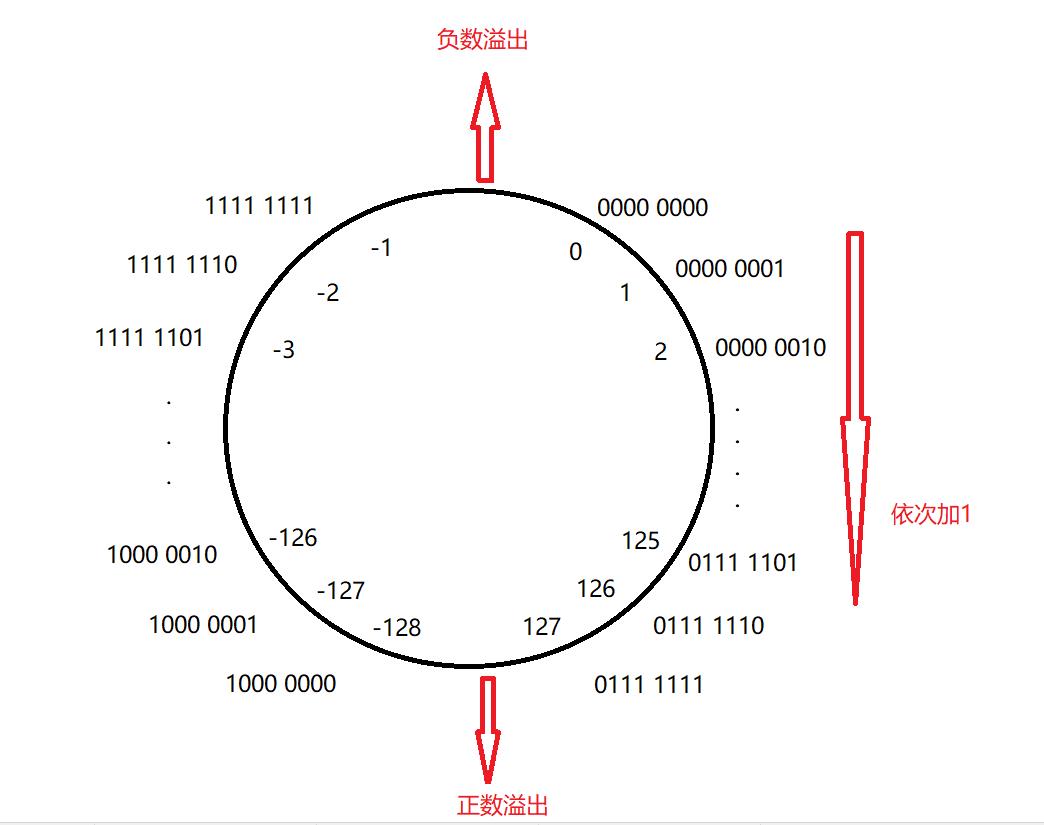
对于8位有符号数，他的范围是[-128 127]，即1000 0000~0111 1111（补码）。

很多人会有疑问，为什么不是1111 1111（原码）即-127（补码1000 0001）

-127-1=-128？怎么得到的

在计算机内用补码进行计算 -127-1=1000 0001+1111 1111（符号位也要相加）

得出来的结果1 1000 0000，有一个溢出位，为了方便理解，此时可以看做成符号位，则他的原码为1 1000 0000所以为-128。事实上规定的是1000 0000是8位下最小的整数值。不要纠结是怎么来的。

如果-128继续减1等于多少呢？

用补码计算，1000 0000+1111 1111 = 0111 1111 这个值就是8有符号数的最大值127。

所以得到：最小值 = 最大值+1；也可以说成最大值 = 最小值-1；

下图是8位二进制有符号数补码变化轮盘。

 

浮点类型存储

	int n = 13;
	float *pFloat = (float *)&n;
	printf("n的值为：%d\\n", n);
	printf("*pFloat的值为：%f\\n", *pFloat);
	*pFloat = 13.0;
	printf("n的值为：%d\\n", n);
	printf("*pFloat的值为：%f\\n", *pFloat);

上述代码的最终输出结果为

n的值为：13
*pFloat的值为：0.000000
n的值为：1095761920
*pFloat的值为：13.000000

为什么加粗的地方是这个值？

根据IEEE二进制浮点数算术标准（IEEE 754）

一个浮点数value = sign*exponent*fraction；

其中sign为符号位，exponent为指数偏移，fraction为分数值。

为了简化表达，定义任何一个二进制浮点数V = (-1)^S*M*2^E;其中S为0时V为正数，为1时V为负数；M表示有效位数字，范围[1,2)；2^E为指数位；

假设10进制下的5.0写成二进制下为101.0，写成上面的形式则为1.01*2^2，指数偏移E相当于小数点需要偏移几位，所以S = 0；M=1.01；E=2；

下图为32位单精度浮点存储模型：

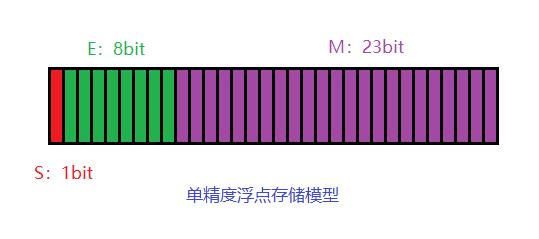
注意E为无符号数，则他的范围是0-255，而在科学计数法里面E的值可以为负数，所以实际上需要加入一个偏移量，取中间值127。上述例子的E=2，则实际值为129，二进制为1000 0001。例如十进制0.5，二进制下为0.1，则转换为上述形式1.0*2^(-1)，S=0;E=-1;M=1.0；实际的E为126, 二进制下为0111 1110。

E全为0的时候表示接近于0；E全为1的时候表示正无穷或者负无穷。

计算机存储M的时候只存储小数点后面的值，默认小数点前的数为1；

---

回答上面的问题

为什么13转化为浮点数变成了0.000000，13在32位int下表示为0x0000000D

0000 0000 0000 0000 0000 0000 0000 1101

对应S=0，E=0000 0000，M=000 0000 0000 0000 0000 1101

S=0，E全为0，表示非常接近0的正数，所以用小数表示就为0.000000；

而通过*pFloat=13.0，使得这块类存空间存储的是浮点类型的值；二进制1101.0；转化为(-1)^0*1.101*2^3，S=0，E=3，M=1.101，E实际上是130。

最终32位存储的结果为：0 1000 0010 101 0000 0000 0000 0000 0000

对应32位整型的值为1095761920。

对于64位双精度浮点类型S：1bit，E：11bit，M：52bit