量子计算学习:从经典计算机到量子计算机
Posted Zccccccc_tz
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了量子计算学习:从经典计算机到量子计算机相关的知识,希望对你有一定的参考价值。
读博做的是量子计算相关方向,现在先学习一波。
经典计算机
| - | 数学方式 | 经典计算机 |
|---|---|---|
| 数据 | 用一串比特(0/1)表示 | 利用电压值的大小来区分(0/1) |
| 操作 | 布尔函数(将所有操作分解为not、or、and) | 用晶体管进行操作(与门、非门、或门) |
| 读取 | 测量比特状态 | 测量电压 |
可以发现,经典计算机是通过电压值通过逻辑门的变换规律,进行数据计算。
量子计算
量子计算与经典区别
由于量子的特点,量子计算和经典计算机有着挺多的区别,在有些地方很不合直觉。
- 经典计算的结果具有确定性,而量子计算的结果具有不确定性(概率性)。
- 量子计算具有非局域性(其中一个现象为量子纠缠),这是量子中最反常的现象。简单来讲就是多量子比特态不可以被单个量子态表示,例如贝尔态。(在后面会经常提到)
下面将从量子计算中的数据、操作、读取分别介绍量子计算。
量子计算中的数据:qubit
单量子态
和经典计算机相同的是,量子计算机也是用比特来表示数据,不过这个单比特用二维的形式表示:
[
α
β
]
\\left[\\begin{matrix}\\alpha \\\\ \\beta\\\\\\end{matrix}\\right]
[αβ]
称为qubit,其中的
α
、
β
\\alpha 、\\beta
α、β均为复数。
那么这里的 α 、 β \\alpha 、\\beta α、β有什么含义吗?
实际上他们模平方分别表示了被观测为0、1的概率,所以我们也可以得到他们的约束条件:
α
2
+
β
2
=
1
\\alpha^2+\\beta^2=1
α2+β2=1(这一点在量子计算的读取上也会提起),任意量子比特均需要满足这一条件。
为了方便表示qubit的状态以及表示qubit的操作,采用狄拉克 (Dirac)符号。
狄拉克 (Dirac)符号
也叫做bra-ket 符号,有以下三种情况:
- ket符号:形如 ∣ 0 > = [ 1 0 ] |0> = \\left[\\begin{matrix}1 \\\\0\\\\\\end{matrix}\\right] ∣0>=[10]、 ∣ 1 > = [ 0 1 ] |1> = \\left[\\begin{matrix}0 \\\\1\\\\\\end{matrix}\\right] ∣1>=[01],又称为左矢。
- bra符号:形如 < 0 ∣ <0| <0∣、 < 1 ∣ <1| <1∣,又称为右矢。
- bar-ket符号:形如 < 0 ∣ 1 > <0|1> <0∣1>。
bra、bra-ket符号的意义会被提到,这里先讲述ket符号。
有了ket符号,我们可以将
[
α
β
]
\\left[\\begin{matrix}\\alpha \\\\ \\beta\\\\\\end{matrix}\\right]
[αβ](
α
[
1
0
]
+
β
[
0
1
]
\\alpha \\left[\\begin{matrix}1 \\\\0\\\\\\end{matrix}\\right] + \\beta \\left[\\begin{matrix}0 \\\\1\\\\\\end{matrix}\\right]
α[10]+β[01])表示为
α
∣
0
>
+
β
∣
1
>
\\alpha |0>+\\beta|1>
α∣0>+β∣1>,表现在二维空间上,则为将矢量分解为两个方向上的和,如图:
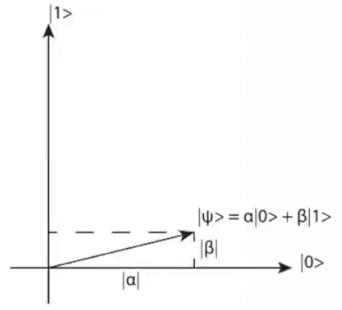
block sphere用于表示单量子比特
block sphere是一个单位二维球面,每一对对应点对应相互正交态矢。布洛赫球面的北极和南极通常分别对应于电子的自旋向上态和自旋向下态标准基矢的0态和1态,反过来也符合
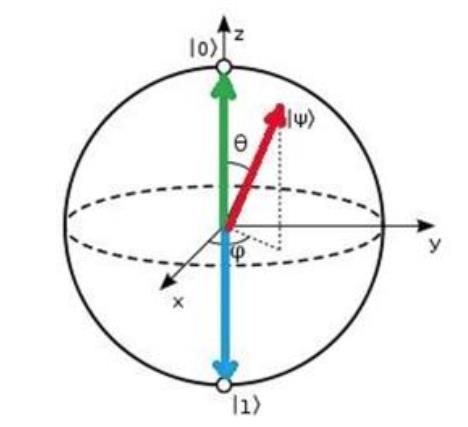
所有的单量子态分布在单位球面上,利用bloch sphere可以更加直观的看到单量子比特通过量子们后的变化,实际为旋转操作(分别绕xyz轴进行旋转)。
根据bloch sphere模型,我们也可以将单量子比特表示为:
e
i
γ
(
c
o
s
θ
2
)
∣
0
>
+
s
i
n
θ
2
)
e
i
φ
∣
1
>
e^{i\\gamma}(cos\\frac{\\theta}{2})|0>+sin\\frac{\\theta}{2})e^{i\\varphi}|1>
eiγ(cos2θ)∣0>+sin2θ)eiφ∣1>
多量子态
前面提到,单量子态为一个二维向量,那么直觉就可以告诉我们多量子态应该是一个 2 n 2^n 2n维的向量,那么如何用数学方式表达?
这里引入了张量积
⊗
\\otimes
⊗ ,用于提升维度,具体运算如下:
[
α
1
β
1
]
⊗
[
α
2
β
2
]
=
[
α
1
[
α
2
β
2
]
β
1
[
α
2
β
2
]
]
=
[
α
1
α
2
α
1
β
2
β
1
α
2
β
1
β
2
]
\\left[\\begin{matrix}\\alpha_1 \\\\ \\beta_1 \\\\ \\end{matrix}\\right] \\otimes \\left[\\begin{matrix}\\alpha_2 \\\\ \\beta_2\\\\\\end{matrix}\\right]= \\left[\\begin{matrix}\\alpha_1 \\left[\\begin{matrix}\\alpha_2 \\\\ \\beta_2\\\\\\end{matrix}\\right]\\\\ \\beta_1 \\left[\\begin{matrix}\\alpha_2 \\\\ \\beta_2\\\\\\end{matrix}\\right]\\\\ \\end{matrix}\\right]= \\left[\\begin{matrix}\\alpha_1\\alpha_2\\\\ \\alpha_1\\beta_2\\\\ \\beta_1 \\alpha_2\\\\ \\beta_1\\beta_2 \\\\ \\end{matrix}\\right]
[α1β1]⊗[α2β2]=⎣⎢⎢⎡α1[α2β2]β1[α2β2]⎦⎥⎥⎤=⎣⎢⎢⎡α1α2α1β2β1α2β1β2⎦⎥⎥⎤
同理我们可以通过张量积的方式构建三量子态。
量子纠缠
可以简单地用数学符号表示:
∃
∣
φ
>
\\exists|\\varphi>
∃∣φ>满足
∣
φ
>
≠
∣
φ
1
>
⊗
∣
φ
2
>
|\\varphi> \\neq |\\varphi_1>\\otimes |\\varphi_2>
∣φ>=∣φ1>⊗∣φ2>。
对应的文字表述则为:存在四维矢量,该矢量不能用两个2维矢量的进行表示。
最常见的就是贝尔态:
∣
φ
+
>
=
1
2
(
∣
00
>
+
∣
11
>
)
|\\varphi^+>=\\frac{1}{\\sqrt{2}}(|00>+|11>)
∣φ+>=21(∣00>+∣11>)、
∣
φ
−
>
=
1
2
(
∣
00
>
−
∣
11
>
)
|\\varphi^->=\\frac{1}{\\sqrt{2}}(|00>-|11>)
∣φ−>=