二叉树类问题框架
Posted 看,未来
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树类问题框架相关的知识,希望对你有一定的参考价值。

前言
花些时间,把这段时间刷的题目分门别类的记录一下基础框架,留待后来人。
每个人的路不同,对我来说,不见得要把大部分时间投入到算法当中,我还是更喜欢系统框架搭建以及底层原理这种大开大合的功法吧。
系列开头先来个最简单的二叉树,使用此框架的前提是:你能把实际问题抽象成为二叉树问题。题目也好,现实问题也罢,都是会有“伪装”的。
解决方案
void traverse(TreeNode* head){
if(head == nullptr){
return;
}
//前序遍历
traverse(head->left);
//中序遍历
traverse(head->right);
//后序遍历
}
应用示例
二叉树最大路径和
后序遍历、
int ans;
int max_lenth(TreeNode* head){
if(head == NULL){
return 0;
}
ans += max(max_length(head->left),max_length(head->right) ) ;
return ans;
}
这是一个后续遍历写法。
前、中序遍历还原二叉树
前序遍历、
//通过前序遍历和中序遍历还原二叉树
TreeNode* rebuild_tree(TreeNode* head,
vector<int> vec1, int preb, int pree,
vector<int> vec2, int mids, int mide)
{
if(mids == mide){
return nullptr;
}
head = new TreeNode(vec1[preb]);
//在中序遍历队列之中将左右分开
int i = mids;
for(;i<mide;i++){
if(vec2[i] == vec1[preb]){
break;
}
}
//做一个赋值构造函数
head->left = rebuild_tree(vec1, pres, i-1, vec2, mids, i-1);
head->right = rebuild_tree(vec1, i+1, pree, vec2, i+1, mid2);
return head;
}
判断两棵二叉树完全相同
前序遍历、
bool isSameTree(TreeNode* root1, TreeNode* root2){
if(root1 == root2){return true;}
if(root1 == nullptr || root2 == nullptr){return false;}
if(root1->val != root->val){return false;}
return isSameTree(root1->left, root2->left) && isSameTree(root1->right, root2->right);
//这个 && 很巧妙哦
}
判断BST的合法性
对于这道题,我想说,不是把握了框架想出了解法,而是把握了框架看懂了代码。。。
反正你让我想,我就只会前序遍历全读到数组里然后判断。。。
#include<iostream>
int ans;
class TreeNode {
public:
TreeNode(int val) {
this->val = val;
left = NULL;
right = NULL;
}
public:
int val;
TreeNode* left;
TreeNode* right;
};
bool isValidBST(TreeNode* root, int max, int min) {
if (root == nullptr) { return true; }
std::cout << root->val << ' ' << max << ' ' << min << std::endl;
if (root->val <= min) { return false; }
if (root->val >= max) { return false; }
return isValidBST(root->left,root->val,min) && isValidBST(root->right, max,root->val);
}
bool isValidBST(TreeNode* root) {
return isValidBST(root, INT_MAX, INT_MIN);
}
int main() {
TreeNode* a = new TreeNode(1);
TreeNode* b = new TreeNode(2);
TreeNode* c = new TreeNode(3);
TreeNode* d = new TreeNode(4);
TreeNode* e = new TreeNode(5);
TreeNode* f = new TreeNode(6);
TreeNode* g = new TreeNode(7);
d->left = b;
b->left = a;
b->right = new TreeNode(0);
d->right = f;
f->left = e;
f->right = g;
std::cout << isValidBST(d);
return 0;
}
BST 遍历框架
相比于二叉树,二叉搜索树的遍历可以做一些优化,没必要每个节点都去转一圈。
void BST(TreeNode* root, int target){
if(root == nullptr){return;}
if(root->val == target){
//dosomething
}
if(root->val > target){
BST(root->left, target);
}
else{
BST(root->left, target);
}
}
完全二叉树的节点数量
满二叉树的节点数量有公式,直接算。
int full_tree(TreeNode* root){
int h = 0;
while(root != null){
root = root->left;
++h;
}
return pow(2, h)-1;
}
普通二叉树就比较尴尬了:
int commen_tree(TreeNode* root){
if(root == null){
return 0;
}
return 1 + commen_tree(root->left) + commen_tree(root->right);
}
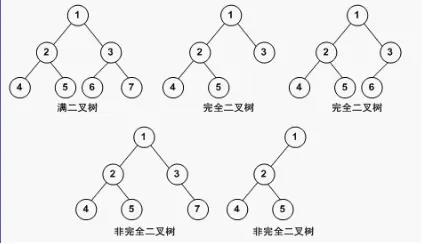
一棵完全二叉树,只有三种可能嘛,要么是一棵满二叉树(图一),要么是一堆满二叉树的结合(图二),要么是两个节点的斜树加上一堆的满二叉树结合(图三)。
所以嘛,直接拆:
int count_node(TreeNode* root){
TreeNode* l = root, r = root;
while(l != nullptr && r != nullptr){
l = l->left;
r = r->right;
hl++;
}
//如果左右子树高度相同
if(l == nullptr && r == nullptr){
return full_tree(root);
}
else{ //那就是不相同咯
return 1+count_node(root->left)+count_node(root->right);
}
}
二叉树节点公共祖先问题
这个嘛,画个图,很自然就想到了后序遍历。
不过这也只是第一步啦,要把节点层层递交上去,所以在遍历的时候有以下几种情况:
1、某节点的所有子节点没有符合条件的
2、某节点就是那俩节点的祖先节点
3、某节点是其中一个节点的祖先节点
情况一很简单,向上递交 null。
情况二其实没那么简单,向上递交,然后呢?情况二本来是可以用两个节点来判断的,但是递交之后,只有一个节点是有值的,另一个节点注定是空。那就和情况三一样了。
所以情况三的处理间接也就是帮情况二在善后了。那么,情况三,将有值的节点递交上去,直到第一层,就OK啦。
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
if(root == nullptr || root == p || root ==q){
return root;
}
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if(left && right){
return root;
}
if(!left && !right){
return nullptr;
}
return right == nullptr?left:right;
}
以上是关于二叉树类问题框架的主要内容,如果未能解决你的问题,请参考以下文章