矩阵乘法AB=C的四种解释
Posted ^_^|
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵乘法AB=C的四种解释相关的知识,希望对你有一定的参考价值。
A * B = C的四种解释
(1) row * col = C[i,j]
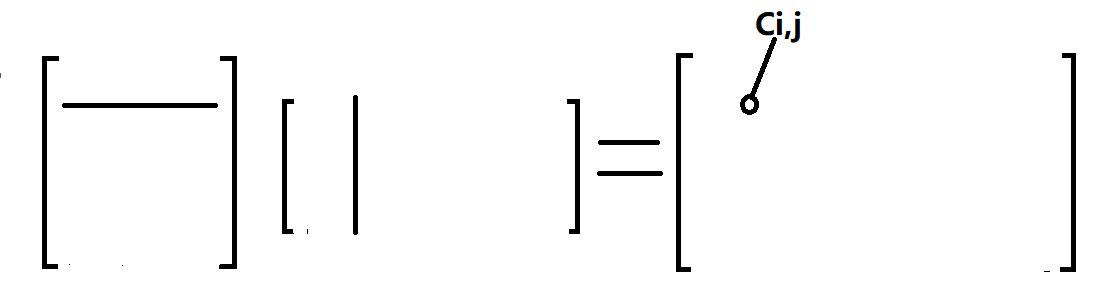
C i , j = ∑ k = 1 n ( a i , k ∗ b k , j ) C_i,_j = \\sum_{k=1}^n(a_i,_k*b_k,j) Ci,j=k=1∑n(ai,k∗bk,j)
(2) A*col(B) = col(C)
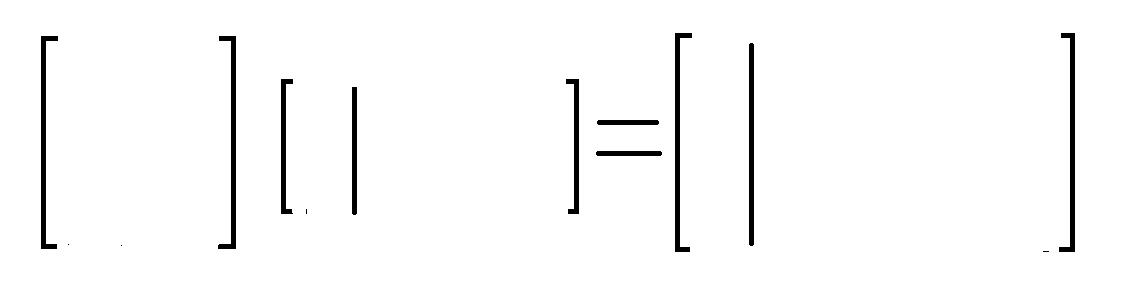
C
的
每
一
列
=
A
∗
(
B
的
对
应
列
)
,
即
C
的
每
一
列
为
A
的
各
列
的
线
性
组
合
C的每一列=A*(B的对应列),即C的每一列为A的各列的线性组合
C的每一列=A∗(B的对应列),即C的每一列为A的各列的线性组合
(3) row(A)*B = row(C)
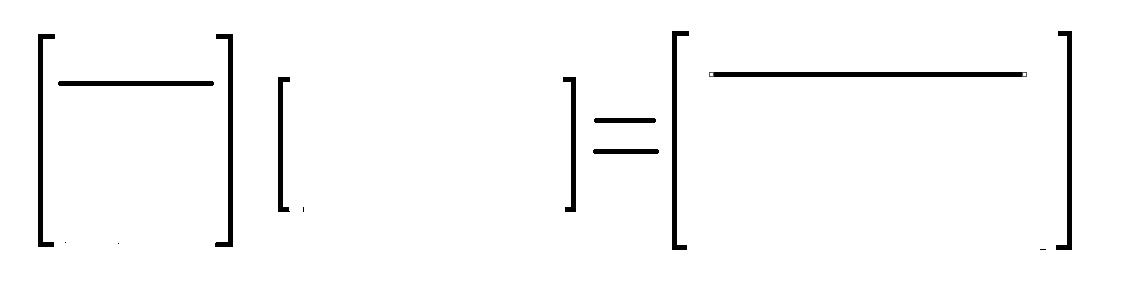
C
的
每
一
行
=
(
A
的
对
应
行
)
∗
B
,
即
C
的
每
一
行
为
A
的
各
列
的
线
性
组
合
C的每一行=(A的对应行)*B,即C的每一行为A的各列的线性组合
C的每一行=(A的对应行)∗B,即C的每一行为A的各列的线性组合
(4) col(A)*row(B)
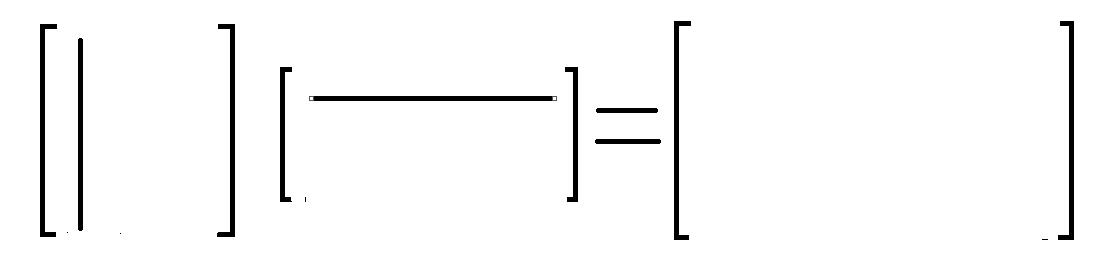
C
=
∑
k
=
1
n
(
c
o
l
k
(
A
)
∗
r
o
w
k
(
B
)
)
C = \\sum_{k=1}^n(col_k(A)*row_k(B))
C=k=1∑n(colk(A)∗rowk(B))
以上是关于矩阵乘法AB=C的四种解释的主要内容,如果未能解决你的问题,请参考以下文章