第2章 关系1
Posted 可能自洽
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第2章 关系1相关的知识,希望对你有一定的参考价值。
一、n元有序组与笛卡尔积
例 证明 A × ( B ∩ C ) = ( A × B ) ∩ ( A × C ) A\\times \\left( B\\cap C\\right) =\\left( A\\times B\\right) \\cap \\left( A\\times C\\right) A×(B∩C)=(A×B)∩(A×C)
取 ( x , y ) ∈ A × ( B ∪ C ) ⇔ x ∈ A , 且 y ∈ B ∪ C ⇔ x ∈ A , 且 y ∈ B 或 y ∈ C ⇔ ( x , y ) ∈ A × B , 或 ( x , y ) ∈ A × C ⇔ ( x , y ) ∈ ( A × B ) ∪ ( A × C ) ⇒ A × ( B ∪ C ) = ( A × B ) ∪ ( A × C ) \\begin{aligned} &取 (x, y) \\in A \\times(B \\cup C)\\\\ &\\Leftrightarrow x \\in A, \\text { 且 } y \\in B \\cup C\\\\ &\\Leftrightarrow x \\in \\boldsymbol{A} \\text {, 且 } y \\in B 或y \\in C\\\\ &\\Leftrightarrow(x, y) \\in A \\times B , 或 (x,y) \\in A \\times C\\\\ &\\Leftrightarrow(x, y) \\in(A \\times B) \\cup(A \\times C)\\\\ &\\Rightarrow A \\times(B \\cup C)=(A \\times B)\\cup(A \\times C) \\end{aligned} 取(x,y)∈A×(B∪C)⇔x∈A, 且 y∈B∪C⇔x∈A, 且 y∈B或y∈C⇔(x,y)∈A×B,或(x,y)∈A×C⇔(x,y)∈(A×B)∪(A×C)⇒A×(B∪C)=(A×B)∪(A×C)
二、关系的基本概念
例 正整数集合 I + I^{+} I+上的“>”关系可定义为
>
=
{
(
x
,
y
)
∣
x
,
y
∈
I
+
,
x
大于
y
}
>=\\left\\{(x, y) \\mid x, y \\in I^{+}, x \\text { 大于 } y\\right\\}
>={(x,y)∣x,y∈I+,x 大于 y}
于是
(
3
,
2
)
∈
>
,
(
2
,
3
)
∉
>
(3,2) \\in>,(2,3) \\notin>
(3,2)∈>,(2,3)∈/>
D
(
>
)
=
I
+
−
{
1
}
,
C
(
>
)
=
I
+
D(>)=I^{+}-\\{1\\}, C(>)=I^{+}
D(>)=I+−{1},C(>)=I+
例 在正整数集 I + I^{+} I+上定义整除关系“ ∣ \\mid ∣”如下
∣
=
{
(
x
,
y
)
∣
x
,
y
∈
I
+
,
x
整除
y
}
\\mid=\\left\\{(x, y) \\mid x, y \\in I^{+}, x \\text { 整除 } y\\right\\}
∣={(x,y)∣x,y∈I+,x 整除 y}
于是
(
2
,
10
)
∈
∣
,
(
2
,
3
)
∉
∣
(2,10) \\in \\mid,(2,3) \\notin \\mid
(2,10)∈∣,(2,3)∈/∣
D
(
∣
)
=
C
(
∣
)
=
I
+
D(\\mid)=C(\\mid)=I^{+}
D(∣)=C(∣)=I+
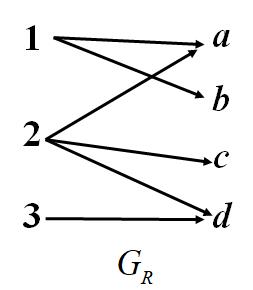
例 令A={1,2,3},B={a,b,c,d},定义关系R={(1,a),(1,b),(2,a),(2,c),(2,d),(3,d)},则该关系R的关系图和关系矩阵分别为
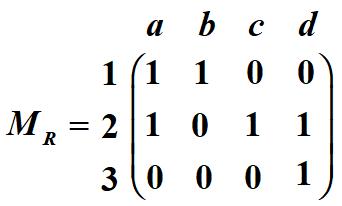
例 令A={1,2,3,4}, 定义关系R= {(1,1),(1,2),(1,3),(2,4),(4,3),(3,1)}给出R的关系图和关系矩阵
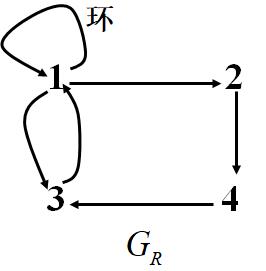
P=
11
→
12
→
24
→
43
→
\\overrightarrow{11} \\overrightarrow{12} \\overrightarrow{24} \\overrightarrow{43}
11122443称为1到3的通路,边数4称为P的长,如果
G
R
G_{R}
GR中x到y有通路,则称G中x可达y
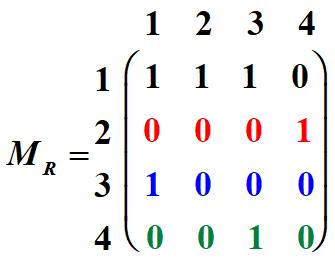
例 令A={1,2,3,4,n}, 定义关系R= {(1,2),(2,3),(3,4),(4,5),(n-1,n),(n,1)},给出R的关系图和关系矩阵
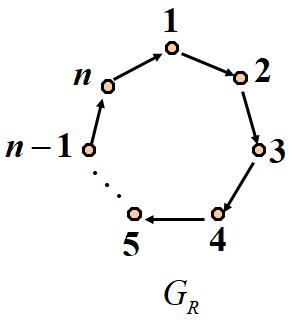
任意两个结点都是相互可达的
1到5有长是4的通路
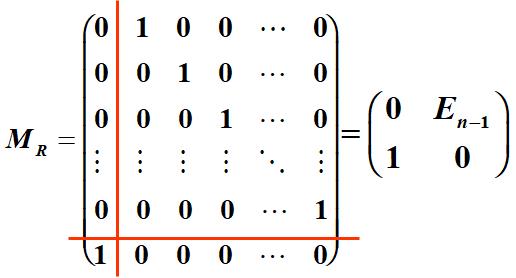
例 设6个程序 p 1 , p 2 , . . . , p 6 p_{1},p_{2},...,p_{6} p1,p2,...,p6,之间的调用关系如下: p 1 R p 2 , p 3 R p 4 , p 4 R p 5 , p 5 R p 2 , p 2 R p 6 , p 3 R p 1 p_{1}Rp_{2},p_{3}Rp_{4},p_{4}Rp_{5},p_{5}Rp_{2},p_{2}Rp_{6},p_{3}Rp_{1} p1Rp2,p3Rp4,p4Rp5,p5Rp2,p2Rp6,p3Rp1给出它们的三种表示
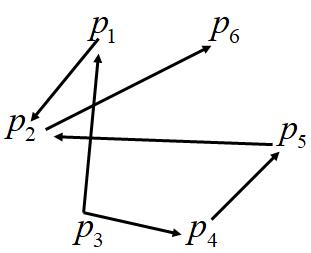
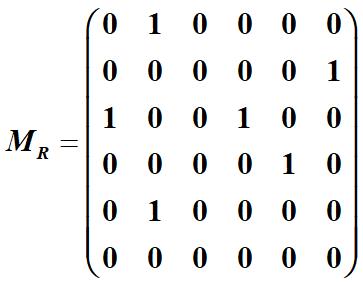
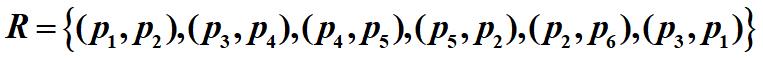
如何判断程序有没有死锁或程序之间有无递归调用等问题就可用该关系来解决
例 设集合X,Y,|X|= m,|Y|= n,问从X到Y有多少不同的二元关系?
注意到X到Y的一个关系就是
X
×
Y
X \\times Y
X×Y的一个子集,于是X到Y的关系的个数就是
X
×
Y
X \\times Y
X×Y的子集个数
但
X
×
Y
X \\times Y
X×Y的所有子集构成了集合
X
×
Y
X \\times Y
X×Y的幂集,于是X到Y的关系个数就是幂集
2
X
×
Y
2^{X \\times Y}
2X×Y的元素个数,
∣
2
X
×
Y
∣
=
2
∣
X
×
Y
∣
=
2
∣
X
∣
×
∣
Y
∣
=
2
m
n
\\left|2^{X \\times Y}\\right| = 2^{|X \\times Y|}=2^{|X| \\times | Y \\mid}=2^{m n}
∣∣2X×Y