python高级算法与数据结构:使用treap实现双索引2

Posted 2021-10-20 tyler_download

上一节我们看到treap结构能对两组数据进行索引，其中一组数据能实现完全排序，另一组数据能实现部分排序，对后者而言就是，我们能快速获取其最大值或最小值。当treap结构出现问题是，我们通过右旋转或是左旋转来进行调整。

有个难点在于，往treap中插入一个元素时，需要保证不破坏对原来两种数据的索引效用。因此插入元素时要执行两个步骤，首先根据元素的第一组数据（在上节例子中就是字符串）以二叉树的方式进行插入，完成后，节点的第二部分数据可能会违背堆的性质，于是我们就需要两种旋转操作来进行调整，具体例子如下：

如上图，左边是要插入的节点，右边是已经形成的treap结构。如果左边节点要出入，那么根据字符串排序，它会成为Bacon的右孩子节点，一旦插入后，根据节点的优先级数值就会违背小堆特性，如下图所示：

从上图看到，Beer节点对应的优先级20小于父节点Bacon，而且它又是父节点的右孩子，因此要进行左旋转，得到结果如下：

如上图，调整一次后，节点可能还不能满足小堆性质，例如Beer的数值就要小于其父节点，同时由于它是左孩子，因此需要进行右旋转，执行后结果如下：

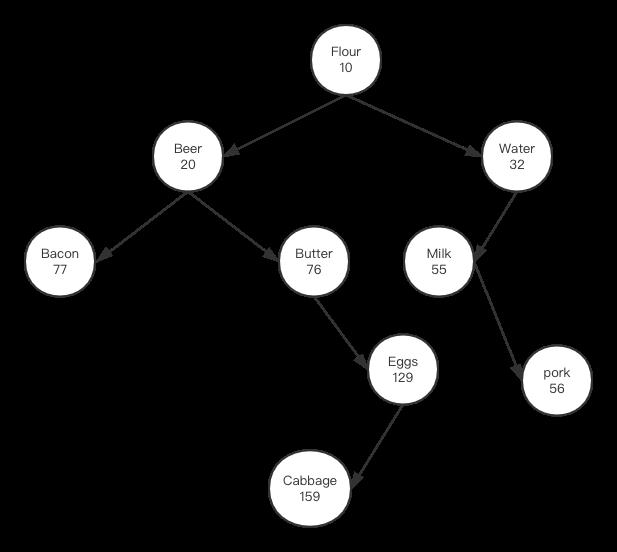
如上图所示，执行到这一步之后所有节点都满足两个条件，他们根据字符串进行了二叉树排序，然后对应的数值都能满足小堆排序，由此插入操作对应代码实现如下：

    def insert(self, key: str, priority: int):
        node: Node = self.root
        parent: Node = None
        new_node = Node(key, priority)

        pdb.set_trace()

        while node is not None:  # 先根据key进行二叉树插入
            parent = node
            if node.key > key:
                node = node.left
            else:
                node = node.right

        if parent is None:
            self.root = new_node
            return
        elif key <= parent.key:
            parent.left = new_node
        else:
            parent.right = new_node
        new_node.parent = parent

        while new_node.parent is not None and new_node.priority < new_node.parent.priority:
            # 持续判断是否违反小堆性质
            if new_node == new_node.parent.left:  # 如果是左孩子那么执行右旋转
                self.right_rotate(new_node)
            else:  # 如果是右孩子则进行左旋转
                self.left_rotate(new_node)

        if new_node.parent is None:
            self.root = new_node

我们构造一个treap结构，然后调用上面代码插入Beer节点试试看：

def setup_treap_insert():
    flour: Node = Node("Flour", 10)
    butter: Node = Node("Butter", 76)
    water: Node = Node("Water", 32)
    bacon: Node = Node("Bacon", 77)
    eggs: Node = Node("Eggs", 129)
    milk: Node = Node("Milk", 55)
    cabbage: Node = Node("Cabbage", 159)
    pork : Node = Node("Pork", 56)

    flour.left = butter
    flour.right = water

    butter.left = bacon
    butter.right = eggs

    water.left = milk

    eggs.left = cabbage

    milk.right = pork

    return flour

root = setup_treap_insert()
treap = Treap()
treap.root = root
treap.insert("Beer", 20)
print_treap(root)

上面代码运行后所得结果如下：

(Flour, 10) parent: None left: (Beer, 20) right: (Water, 32)
(Beer, 20) parent: (Flour, 10) left: (Bacon, 77) right: (Butter, 76)
(Bacon, 77) parent: (Beer, 20) left: None right: None
(Butter, 76) parent: (Beer, 20) left: None right: (Eggs, 129)
(Eggs, 129) parent: (Butter, 76) left: (Cabbage, 159) right: None
(Cabbage, 159) parent: (Eggs, 129) left: None right: None
(Water, 32) parent: (Flour, 10) left: (Milk, 55) right: None
(Milk, 55) parent: (Water, 32) left: None right: (Pork, 56)
(Pork, 56) parent: (Milk, 55) left: None right: None

从输出结果看，它跟我们前面分析完全一致。接下来我们看看节点的删除操作。删除某个节点时，我们给被删除的节点赋予一个很大值，然后对其不断进行push_down操作，直到它成为叶子节点后，将它与treap断开连接，假设我们要把Butter节点删除，我们先将它的值设置为无穷大：

如上图，要删除Butter节点，先把它的值设置为无穷大后，执行push_down操作，执行一次push_down后结果如下：
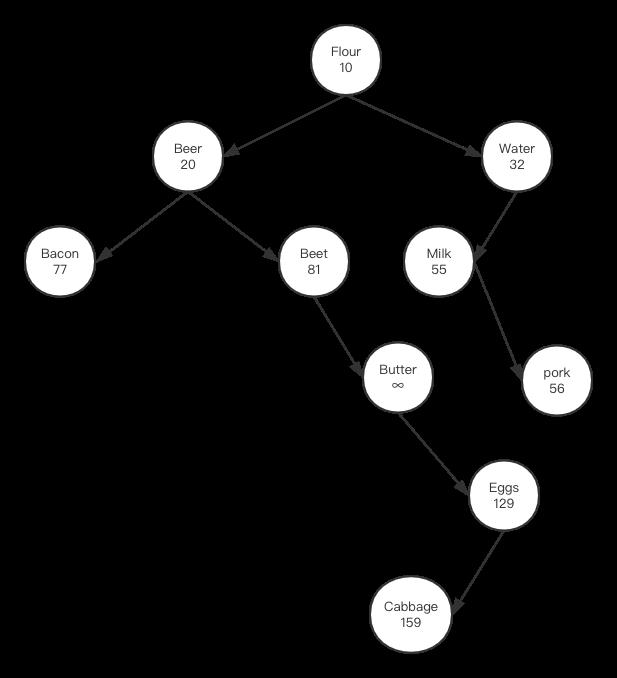此时它还不是叶子节点，因此需要再次执行push_down,结果如下：

此时它依然不是叶子节点，因此再次执行push_down，得到结果如下：

执行到这一步后，我们看到它已经成为叶子节点，此时将它和父节点断开，那就相当于把它从treap结构中删除，我们看看相应代码实现：

    def remove(self, key):
        node = self.search(key)  #查找包含给定字符串的节点
        if node is None:
            return False

        if node.is_root() and node.is_leaf(): #如果只有一个节点那么将treap设置为空
            self.root = None
            return True

        while not node.is_leaf():#把当前节点优先级设置为无穷大,因此要把左右孩子中优先级较小的那个进行旋转
            if node.left is not None and (node.right is None or node.left.priority < node.right.priority):
                self.right_rotate(node.left)
            else:
                self.left_rotate(node.right)

            if node.parent.is_root():
                self.root = node.parent

        if node.parent.left is node:
            node.parent.left = None
        else:
            node.parent.right = None

        return True

我们构造一个treap，然后调用上面代码删除一个节点试试：

def setup_treap_remove():
    flour: Node = Node("Flour", 10)
    beer: Node = Node("Beer", 20)
    butter: Node = Node("Butter", 76)
    water: Node = Node("Water", 32)
    eggs: Node = Node("Eggs", 129)
    milk: Node = Node("Milk", 55)
    cabbage: Node = Node("Cabbage", 159)
    pork: Node = Node("Pork", 56)
    beet : Node = Node("Beet", 81)

    flour.left = beer
    flour.right = water
    beer.right = butter
    water.left = milk

    butter.left = beet
    butter.right = eggs
    eggs.left = cabbage

    milk.right = pork

    return flour
root = setup_treap_remove()
treap = Treap()
treap.root = root
treap.remove("Butter")
print_treap(root)

代码运行后，所得结果如下：

(Flour, 10) parent: None left: (Beer, 20) right: (Water, 32)
(Beer, 20) parent: (Flour, 10) left: None right: (Beet, 81)
(Beet, 81) parent: (Beer, 20) left: None right: (Eggs, 129)
(Eggs, 129) parent: (Beet, 81) left: (Cabbage, 159) right: None
(Cabbage, 159) parent: (Eggs, 129) left: None right: None
(Water, 32) parent: (Flour, 10) left: (Milk, 55) right: None
(Milk, 55) parent: (Water, 32) left: None right: (Pork, 56)
(Pork, 56) parent: (Milk, 55) left: None right: None

从打印的结果看，与我们上面分析的结果是一致的。以上实现的treap结构和操作有一个问题，那就是容易产生左右子树不平衡，后面我们再看如何处理这个问题。Treap结构可以提供不少方便的接口，例如top, peek, update等，相关接口实现如下：

    def top(self):
        if self.root is None:
            return None

        key = self.root.key
        self.remove(key)
        return key

其他接口的实现相对简单，就是update要复杂一些，更新节点时可以先把节点remove掉，然后修改节点里面的内容，接着再调用insert把节点插入即可，完整代码请查看https://github.com/wycl16514/python-.git，更多详细精彩内容请点击这里