void swap(int* left, int* right)
{
	int tmp = *left;
	*left = *right;
	*right = tmp;

}

void BubbleSort(int arr[], int n)
{
	for (int i = 0; i < n - 1; i++)//总共进行n-1趟
	{
		for (int j = 0; j < n - 1 - i; j++)//每一趟进行n-1-i的比较
		{
			if (arr[j] > arr[j + 1])
			{
				swap(&arr[j], &arr[j + 1]);
			}
		}
	}
}

冒泡排序的总结：

1. 时间复杂度： O(N^2) 。

2. 空间复杂度：O(1) ，冒泡排序不需要开额外的空间。3.

稳定性：稳定

快速排序

基本思想：

快速排序是 Hoare 于 1962 年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

将区间按照基准值划分为左右两半部分的常见方式有：

1. hoare版本

2. 挖坑法

3. 前后指针版本

1.hoare版本

先找基准值，一般是以最左边的值作为基准值，找出基准值后，在设两个指针left和righ，

1.首先从right所指位置从后往前找到第一个比基准值小的值，

2.再从left所指位置往后搜索找到第一个大于基准值的值。

3在将left指向的值和right指向的值进行交换，重复以上三个步骤直到left==right为止。

注意：如果是以left为基准值，必须让right先走，不然最后相遇的位置不一定比基准值小。

为什么相遇的位置一定会比基准值小？

代码：

void swap(int* left, int* right)
{
	int tmp = *left;
	*left = *right;
	*right = tmp;

}


int Partition1(int arr[], int left, int right)
{

	int key = left;	//设定基准值的位置
	while (left < right)
	{
		//right找出比基准值小的值
		// 8,4,5,2,5,1,5,2 
		while (left < right && arr[right] >= arr[key])
		{
			right--;
		}
		//left找出比基准值大的值
		while (left < right && arr[left] <=arr[key])
		{
			left++;
		}

		swap(&arr[left], &arr[right]);
	}
	//最后交换基准值和相遇位置的值
	swap(&arr[key], &arr[left]);
	return left;
}

当我们排完一序后，position的左边全小于position位置的值，position的右边值全大于position位置的值，所以此时的position位置的值，就是在它在有序序列中的位置，我们只需要对它的左边和右边进行如上述的排序，找到值在有序序列中相对应的位置，所以这时候我们需要用递归的方式进行对每个左右序列进行排序，直到left>=right即结束排序。

上诉过程代码如下：

void QuickSort(int arr[], int start, int end)
{
	if (start >= end)
	{
		return;
	}
	int position = Partition1(arr, start, end);
	QuickSort(arr, start, position - 1);
	QuickSort(arr, position + 1, end);
	
}

2.挖坑法

其中上面的hoare版本（position1函数），也可以用挖坑法或者前后指针的方法来替代hoare版本。下面我将分别讲一下挖坑法和前后指针的具体过程和代码实现。如果三个版本中一定要掌握一个，推荐掌握挖坑法，因为它的逻辑较容易理解。

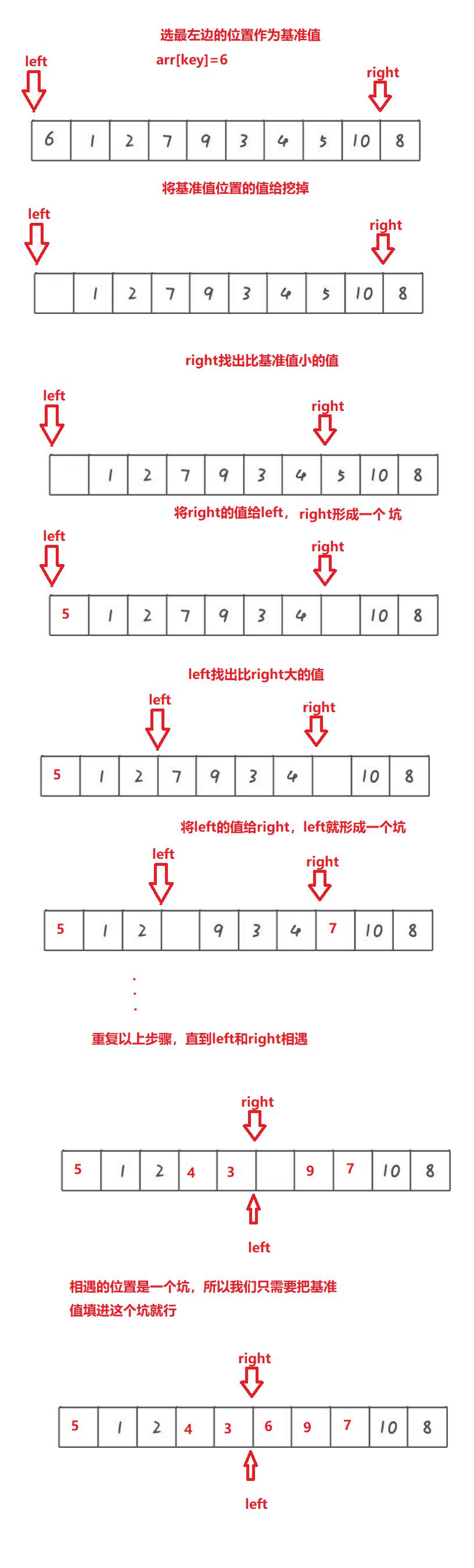
代码：

int Partition(int arr[], int left, int right)
{
	int key = arr[left];//将key先作为一个坑
	while (left < right)
	{ 
        //right找出比key小的值
		while (left < right && arr[right] >= key)
		{
			right--;
		}
        //将right的值填充到坑中，right形成一个坑
		arr[left] = arr[right];
         //left找出比key大的值
		while (left < right && arr[left] <= key)
		{
			left++;
		}
       
        //将left的值填充到坑中，left形成一个坑
		arr[right] = arr[left];
	}
     //最后将key填充到相遇的坑位中
	arr[left] = key;
	return left;
}

3 .前后指针法

以最左边的值作为key值，然后创建prev和cur，prev首先指向序列的第一个值，cur指向的是序列第二个值，让cur走，找出比key小的值，找到了比key小的值，则pre就走一步，然后cur与prev进行交换，重复以上步骤，直到cur遍历完序列，最后将prev与key进行交换即可。

代码：

int Partition3(int arr[], int left, int right)
{
	int key = left;
	int prev = left;//以最左边设为prev
	int cur = left + 1;//最左边第二个值设为prev
	while (cur <= right)
	{
		//如果cur小于key且++完后的prev不等于cur
		//才进去交换
		if (arr[cur] < arr[key] && ++prev != cur)
		{
			swap(&arr[cur], &arr[prev]);
		}
		cur++;
	}
	//最后key和prev才交换
	swap(&arr[key], &arr[prev]);
	return prev;
}

快排优化

快排什么时候最快呢？

当每趟排完序之后，基准值位于序列的最中间的时候，此时的快排是最快的，因为没趟排序left和right遍历的总共的数据为n，所以每趟的排序为的时间复杂度为O(n),当每次基准值都位于序列的最中间的时候，相当于每趟排序都把序列分为2份，当子序列只剩下1的时候，排序结束。所以时间复杂度为O(log2n)(log2是以2为底)，总的时间复杂度为O(nlog2n).

快排什么时候最慢呢？

当序列有序（升序或逆序）的时候，每趟排序的基准值都得放在最前或最后，此时的快排是最慢的。此时快排的效率为O(n^2),

优化一：三数取中

在每趟排序中，为了防止最坏的情况的出现，我们可以采用三数取中的方式解决这个问题，三数取中是拿出left和right，再加上序列中最中间的值mid，然后再将这三个数进行比较，拿这三个值中的第二大的值作为基准值，这样我们就可以避免最坏的情况出现。

取出第二大的值：

//三数取中的函数
int MiddleNum(int arr[], int left, int right)
{
	int mid = (left + right) / 2;
	if (arr[mid] > arr[left])
	{
		if (arr[mid] < arr[right])
		{
			return mid;
		}
		else if (arr[left] > arr[right])
		{
			return left;
		}
		else {
			return right;
		}
	}
	else {
		if (arr[mid] > arr[right])
		{
			return mid;
		}
		else if (arr[right] > arr[left])
			return left;
		else {
			return right;
		}
	}
}

int Partition2(int arr[], int left, int right)
{
	int mid = MiddleNum(arr, left, right);
	swap(&arr[left], &arr[mid]);
	int key = arr[left];
	while (left < right)
	{
		while (left < right && arr[right] >= key)
		{
			right--;
		}
		arr[left] = arr[right];
		while (left < right && arr[left] <= key)
		{
			left++;
		}
		arr[right] = arr[left];
	}
	arr[left] = key;
	return left;
}

优化二：小区间优化

在进行快速排序的时候，我们发现越到后面的排序中，小区间只剩下少量的值，但是递归次数也会很多，为了减少递归次数，所以我们可以将最后的小区间只剩下有限个值进行插入排序（10个值，20个值等等），这样就可以减少我们后面的递归。

优化代码如下：

void QuickSort(int arr[], int start, int end)
{
	if (start >= end)
	{
		return;
	}

	//小区间只剩下10个值就进行插入排序
	if (end - start > 10)
	{
		int position = Partition3(arr, start, end);
		QuickSort(arr, start, position - 1);
		QuickSort(arr, position + 1, end);
	}
	else
	{
		InsertSort(arr + start, end - start + 1);
	}
}