算法——八皇后问题（递归回溯实现）

Posted 2021-10-19 高、远

【1】代码：

package algorithm.queen;

import java.io.OptionalDataException;

public class Queen {

    private static final int max = 8;
    //用一维数组储存每一次成功的皇后位置
    /**
     * arr的下标表示第几行，里面储存的数据是第几列
     */
    private static int[] arr = new int[max];
    //计数，看最后有多少种结果
    private static int sum = 0;

    public static void main(String[] args) {
        queen(0);
        System.out.println();
        System.out.println();
        System.out.println();
        System.out.println(sum);
    }

    //递归回溯
    public static void queen(int n) {
        if (n == max) {//n = max的时候相当于 第max个皇后已经放好了，正在放置第max+1个皇后,直接return就行
            //没找到一种 ，即n == max的时候就将刚才找到的这一种打印出来
            prin();
            //每找到一种就++
            sum++;
            //一种排法已经找完，直接return
            return;
        }
        //第n行的每一列都要试一下
        for (int i = 0; i < max; i++) {
            arr[n] = i;
            //如果检验成功
            if (isValid(n)) {
                //回溯
                queen(n + 1);
            }
            //如果冲突就回到就继续循环试试下一列
        }
        //如果这个皇后将这一行的所有列都检验玩了都找不到合适的位置放置，就回溯到上一个皇后的位置
        return;
    }

    //打印结果：
    public static void prin() {
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }

    //检查位置是否正确
    //跟前面的所有行进行检验
    public static boolean isValid(int n) {
        for (int i = 0; i < n; i++) {
            //不合法
            if (arr[n] == arr[i] || Math.abs(i - n) == Math.abs(arr[i] - arr[n])) {
                return false;
            }
        }
        return true;
    }
}

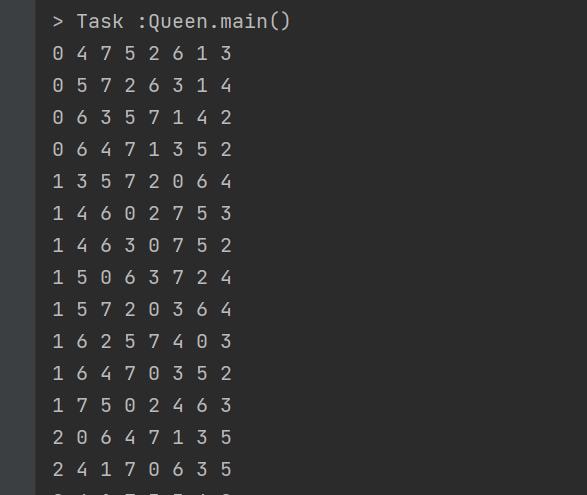
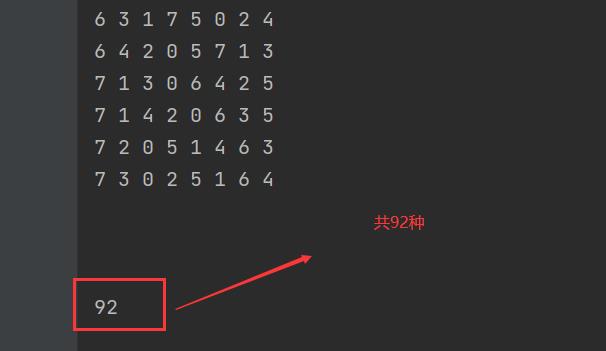
【2】运行结果：