余弦相似性和相关
Posted 飞凡可期
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了余弦相似性和相关相关的知识,希望对你有一定的参考价值。
person相关
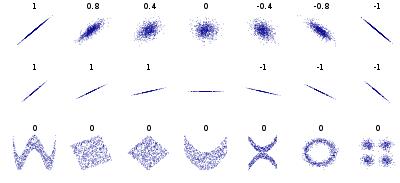
首先的概念是相关性是衡量线性关系,而非“非线性”关系。如上图,二维平面点集合
- 第一行可以发现是围绕直线的(x,y)点,比如(1,1.1) 和(1.1,1)几乎为1,反之最右侧的是(-1,1.1) (-1.1,1),在直观上,他们两队坐标是各自相关的,却是-1和1差距,在两个极端。但实际还是一回事儿,反应了两个变量x,y的"线性相关"程度。—同向增长,反向增长。 介于中间的0.8/0.4这些点则是弱线性相关,增长反向不总一致或反向。0处则是完全无规律。
- 第二行,发现相关方向和斜率无关(线的方向),也即同向增长并不意味着同比增长。
- 第三行,非线性相关的比如w曲线,圆形等。相关和都是0,反应非线性关系,相关性这个简单的标量衡量不了。
cosine相关
将x轴点比如[1,2,3,4],y轴点[0.1,0.2,0.3,0.4]各作为多维矢量,则cosine相关正好是x,y矢量的张角cos值,恰好也在-1,1之间。
- 这反应了相关从多维空间中就是反应两个矢量方向的相对路径,是同向、反向还是正交等等。
- 这也解释了为啥是反应线性关系,而非非线性。因为两个多维矢量,无论多么高维度,线与线的相对关系也只是共一个多维平面的“角度”关系,远不能表达曲面,纠缠等复杂信息。。。也完全没有幅度、接近程度的度量信息。。。逼近都在-1,1范围,更像是归一化的“相位“特性。
数学上,person和cosine二者是等价的。理解上差异只是一个代数、一个几何角度。
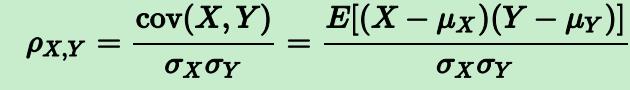
XY两个分布的相关性。
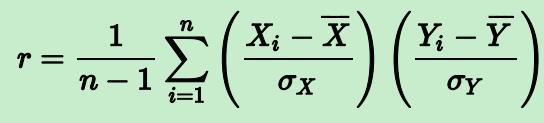
通过样本抽样点归一化的有偏估计来得。
- 注意点是:r相关性值在不同领域的差异天差地别,决不能武断认为0.9相关性就是高。这和高斯分布、置信区间的5%,10%概率不同。典型的许多社会科学0.9已经是很高相关性了,但在自然科学中比如仪器的震动相关性0.9也不算什么。

- 常用的距离度量是1-rou,[0,2]; 1时候是相关性0(线性正交)。
实际问题:相邻包的信道相关性
- 问题:采集相邻20ms间隔的两个包,取同样判断的CFR, OFDM制式,各30个子载波。
- 问:现在发现有的邻包相关系数下降厉害比如0.9落到0.2?
- 分析: 默认前一包{Xi}序列,后一个包{Yi}序列,随着频域展开。XY相关反应各个频点上随时间的变法关系?
- 那么问题来了,现在发现由于同步算法、或者终端频偏原因,其实频域点未必是对齐的。这个0.2相关性能代表实际时间上相关吗?
- 答案:不能。因为标量相关(person或者cos)只反映线性关系。你的频域错开破坏了对齐性,比如{0.1,0.2,0.3}和{1,2,3}是高相关的,0.9999999;而错位{0.2,0.3,0.1}和{1,2,3}呢,相关性只有0.78了。显然这不能判定两个序列不相关,尤其当它足够长的时候。
- 相关性局限性很明显。所以需要考虑变换域后对齐后做相关。或者替换更高维度的相关度量。
多说两句
假设检验
假设完全不相关,然后检测样本的相似度!很好理解,非垂直序列,便认为不能摆脱相关性!反证明相关,, 或者验证无关的方法。
- 验证0假设是否为真,即相关系数rou是否等
于 0, 。 - 在给定自信水平下,构建围绕rou的置信空间。
随机采样方法–显著性检验
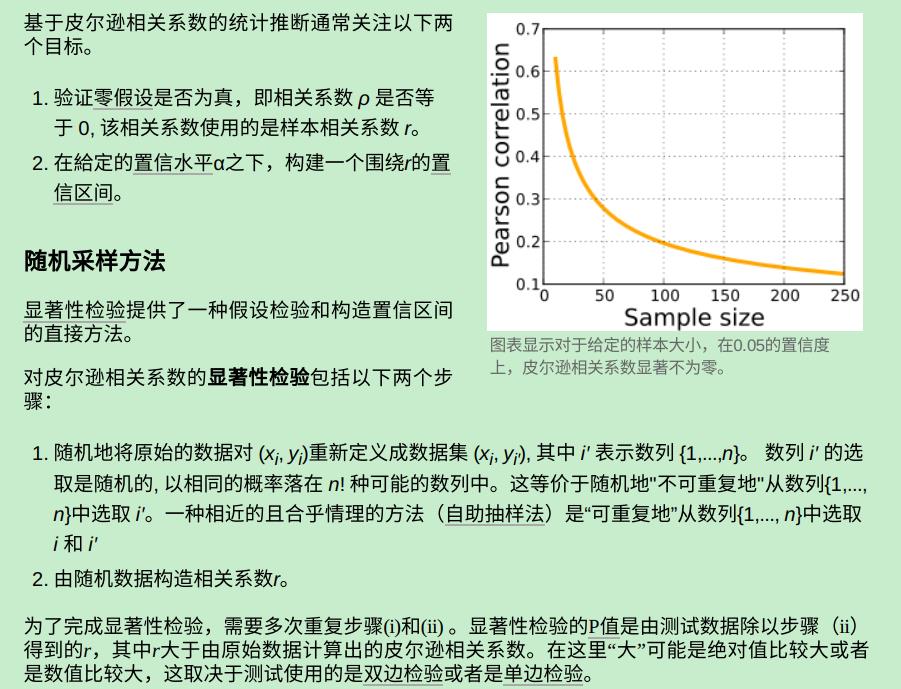
随机采样构造序列,针对序列计算相关rou,通过测试数据除以rou得到显著性水平P,得到相关程度。。。和假设检验相反,证真的。假设检验是证伪的(反例证明相关),这里直接显著性大小。。。通过分布来确定比如5%的置信的区间范围。
以上是关于余弦相似性和相关的主要内容,如果未能解决你的问题,请参考以下文章