LeetCode 007 数与位系列
Posted Al_tair
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LeetCode 007 数与位系列相关的知识,希望对你有一定的参考价值。
数与位(二)
大家好!我是小笙!数与位(一)系列落下帷幕,开始新的征程数与位(二)!大家一起加油呀!!
数与位(二)系列题型如下
数与位系列二
数与位(258,171,357)
258. 各位相加
给定一个非负整数 num,反复将各个位上的数字相加,直到结果为一位数。
示例:
输入: 38
输出: 2
解释: 各位相加的过程为:3 + 8 = 11, 1 + 1 = 2。
由于 2 是一位数,所以返回 2。
进阶: 你可以不使用循环或者递归,且在 O(1) 时间复杂度内解决这个问题吗?
方法一:遍历(MyCode)
我想的是通过两层while来求得该解
第一个while我是用来判断是否运算到一位数
第二个while我是用来判断num的每位数是否已经累加完
class Solution {
public int addDigits(int num) {
int sum = 0;
while(num/10 != 0){
while(num != 0){
sum += num % 10;
num = num / 10;
}
num = sum;
sum = 0;
}
return num;
}
}
执行用时:1 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:35.3 MB, 在所有 Java 提交中击败了93.06%的用户
方法二:秒!(Other’sCode)
class Solution {
public int addDigits(int num) {
return (num - 1) % 9 + 1;
}
}
171. Excel 表列序号
给你一个字符串 columnTitle ,表示 Excel 表格中的列名称。返回该列名称对应的列序号。
例如,
A -> 1
B -> 2
C -> 3
…
Z -> 26
AA -> 27
AB -> 28
…
示例 1:
输入: columnTitle = “A” 输出: 1 示例 2:
输入: columnTitle = “AB” 输出: 28 示例 3:
输入: columnTitle = “ZY” 输出: 701 示例 4:
输入: columnTitle = “FXSHRXW” 输出: 2147483647
提示:
1 <= columnTitle.length <= 7
columnTitle 仅由大写英文组成
columnTitle 在范围 [“A”, “FXSHRXW”] 内
方法一:27进制(MyCode)
本质上就是27进制数,只不过每个数用字母替代
class Solution {
public int titleToNumber(String columnTitle) {
int n = columnTitle.length();
int sum = 0;
for(int i=0;i<=n-1;i++){
sum += (columnTitle.charAt(i)+1-'A')*Math.pow(26,n-1-i);
}
return sum;
}
}
执行用时:1 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:38.2 MB, 在所有 Java 提交中击败了83.84%的用户
357. 计算各个位数不同的数字个数
给定一个非负整数 n,计算各位数字都不同的数字 x 的个数,其中 0 ≤ x < 10n 。
示例:
输入: 2
输出: 91
解释: 答案应为除去 11,22,33,44,55,66,77,88,99 外,在 [0,100)区间内的所有数字。
方法一:暴力解法(MyCode)
我不确认我的代码一定正确
原因是时间复杂度太大,导致在运行最后一个测试案例的时候时间超时
但是我还是想把我的代码展现出来,也是尽力了
代码思路:
无非就是每传入一个数字检查它的重复性 时间复杂度O(n^3)
class Solution {
public int countNumbersWithUniqueDigits(int n) {
boolean bool = false;
int count = 0;
for(int i=0;i<Math.pow(10,n);i++){
bool = repeat(i);
if(bool == false){
count++;
}
}
return count;
}
public boolean repeat(int num){ // 计算数字的重复性
String s = String.valueOf(num);
int n = s.length();
if(n == 1) return false;
for(int i=0;i<n-1;i++){
for(int j=i+1;j<n;j++){
if(s.charAt(i) == s.charAt(j)){
return true;
}
}
}
return false;
}
}
方法二:DP(Other’sCode)
思路是别人的,但是代码都是自己完成的!
/**
别人的思路:
* 排列组合:n位有效数字 = 每一位都从 0~9 中选择,且不能以 0 开头
* 1位数字:0~9 10
* 2位数字:C10-2,且第一位不能是0 9 * 9
* 3位数字:C10-3,且第一位不能是0 9 * 9 * 8
* 4位数字:C10-4,且第一位不能是0 9 * 9 * 8 * 7
* ... ...
* 最后,总数 = 所有 小于 n 的位数个数相加
*/
class Solution {
public int countNumbersWithUniqueDigits(int n) {
if (n == 0) return 1;
int result = 10, next = 9 * 9;
for (int i = 2; i <= n; i++) {
result += next;
next *= 10 - i; // 记录下一个要乘的数字
}
return result;
}
}
简单数学题(29)
29. 两数相除
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。 返回被除数 dividend 除以除数 divisor 得到的商。
整数除法的结果应当截去(truncate)其小数部分,例如:truncate(8.345) = 8 以及 truncate(-2.7335) = -2
示例 1:
输入: dividend = 10, divisor = 3
输出: 3
解释: 10/3 = truncate(3.33333…) =truncate(3) = 3 示例 2:
输入: dividend = 7, divisor = -3
输出: -2
解释: 7/-3 = truncate(-2.33333…)= -2
提示:
被除数和除数均为 32 位有符号整数。 除数不为 0。 假设我们的环境只能存储 32 位有符号整数,其数值范围是 [−231, 231 − 1]。本题中,如果除法结果溢出,则返回 231 − 1。
方法一:加法代替(MyCode)
这个题目初看特别简单,难就难在边界的处理 - 2147483648
class Solution {
public int divide(int dividend, int divisor) {
if (dividend == -2147483648 && divisor == -1) return 2147483647; //只有这种情况会溢出
if (dividend == -2147483648 && divisor == 2) return -2147483648/2;
int num = dividend,num2 = divisor;
if(dividend > 0){
num = -1*dividend;
}
if(divisor > 0){
num2 = -1*divisor;
}
int count=0;
while(num <= num2){
count++;
num = num - num2;
}
if((dividend<0 && divisor>0) || (dividend>0 && divisor<0)){
return -1*count;
}else{
return count;
}
}
}
执行用时:2807 ms, 在所有 Java 提交中击败了5.00%的用户
内存消耗:35.4 MB, 在所有 Java 提交中击败70.56%的用户
方法二:二进制除法(Other’sCode)
class Solution {
public int divide(int dividend, int divisor) {
boolean sign = dividend > 0 ^ divisor > 0; // 符号标志位
long a = Math.abs((long) dividend);
long b = Math.abs((long) divisor);
long res = 0;
int digit = 0;
while (a >= b << digit) digit++;
while (a >= b) {
if (a >= b << digit) {
a -= b << digit;
res += (long) 1 << digit;
}
digit--;
}
res = sign ? -res : res;
// 限幅
if (res < Integer.MIN_VALUE) return Integer.MIN_VALUE;
if (res > Integer.MAX_VALUE) return Integer.MAX_VALUE;
return (int) res;
}
}
快速幂(50)
50. Pow(x, n)
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。
示例 1:
输入:x = 2.00000, n = 10 输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3 输出:9.26100
示例 3:
输入:x = 2.00000, n = -2 输出:0.25000 > 解释:2-2 = 1/22 = 1/4 = 0.25 /
提示:
-100.0 < x < 100.0
-231 <= n <= 231-1
-104 <= xn <= 104
MyCode
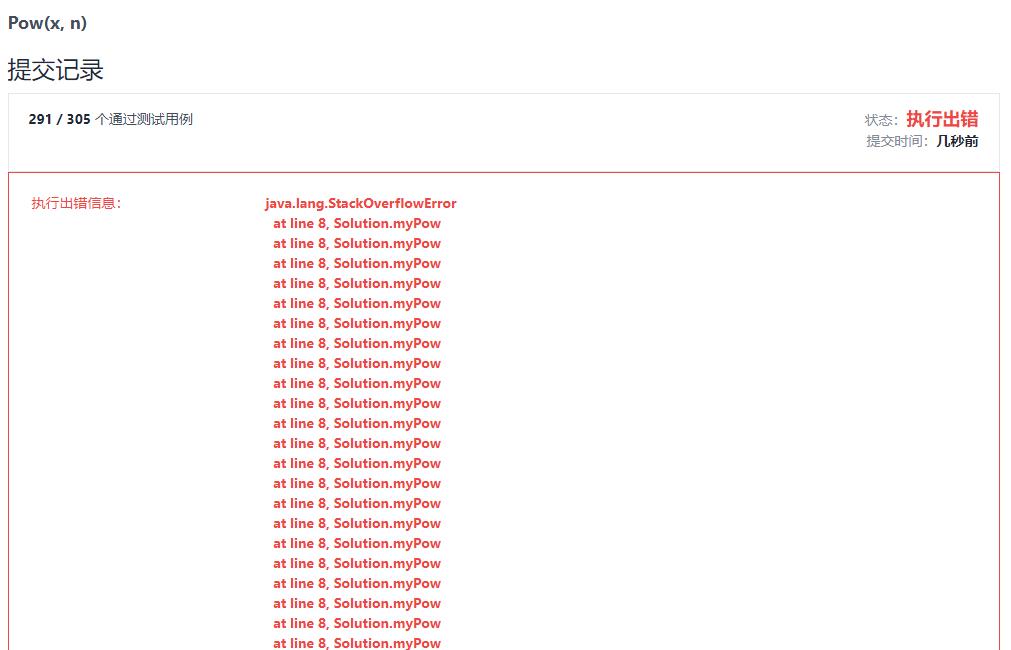
我提交了,但是由于递归导致栈溢出,但是我还是想把我的代码分享出来
测试也291/305 大部分是通过测验的正确与否未可知
class Solution {
public double myPow(double x, int n) {
if(x == 0.0) return 0.0;
if(n == 0) return 1.0;
double sum = 0.0;
if(x>0 && n>=1){
if(n == 1) return x;
return x*myPow(x,n-1);
}else if(x<0 && n>=1){
if(n == 1) return x;
return x*myPow(x,n-1);
}else if(x>0 && n<=-1){
if(n == -1) return 1/x;
sum = 1/x*myPow(x, n+1);
return sum;
}else{
if(n == -1) return 1/x;
sum = 1/x*myPow(x, n+1);
return sum;
}
}
}
然后想解决办法就是优化递归次数
方法二:快速幂 + 递归(Other’sCode)

class Solution {
public double myPow(double x, int n) {
long N = n; // 防止出现 -2147483648 的问题
return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N); // 分治 秒!
}
public double quickMul(double x, long N) {
if (N == 0) return 1.0;
double y = quickMul(x, N / 2);
return N % 2 == 0 ? y * y : y * y * x; // N 很关键,判断是否是被整除或者余数为1
}
}
以上是关于LeetCode 007 数与位系列的主要内容,如果未能解决你的问题,请参考以下文章