一线业务前端如何快速学习算法:直击本质与拆解大法
Posted Jtag特工
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一线业务前端如何快速学习算法:直击本质与拆解大法相关的知识,希望对你有一定的参考价值。
一线业务前端如何快速学习算法:直击本质与拆解大法
随着传说中的越来越卷的时代的到来,算法被用得越来越多。比起相对来说时间更可控的架构和工具等角色,一线业务前端业务压力大,琐碎任务多且急,要么是一个复杂动画只有一天开发时间,要么是跟视觉设计同学为几个像素调一下午,要么是突然线上有用户反馈有问题了必须马上解决,很难有大的整块时间去学习和练习算法。
但是,一线同学也有自己的优势。首先是动手能力强,也就是码代码的能力强,要不然早就被产品经理、运营、后端、设计、测试等同学喷死了;其次是定位与调试问题的能力强,要是只能写bug不能解bug还需要队友擦屁股,估计早被开除了吃不了一线这碗饭。
这样我们扬长避短,避免学习太多技术细节,只学算法最本质的理论,然后剩下的自己造轮子实操。

有同学会问,这样会不会陷入低水平重复之中啊?
答案是不会的。为什么?因为绝大多数复杂的问题没有简单的解法。
那么针对复杂问题我们造不动轮子,怎么办?
办法很简单,拆解大法。
第一步:我们把这个复杂问题,拆解成若干个简单的子问题和一个或多个较难的子问题。
第二步:将简单的子问题解决掉
第三步:将剩下的困难的子问题再拆解成简单子问题和较难的子问题,重复第二步。直至困难问题已经被拆解到足够小,我们就只用少量时间学习这最困难的一点就好了。
很多同学不信就这么简单,那么事实胜于雄辩,我们举例子。
原理:小的放左边,大的放右边
我们先来个一种排序方法原理的作为例子,这个原理实在是不能再简单了,叫做,把小的放左边,大的放右边。
我们把这个基本原理细化一下。
如果来一个新数,我们把它放到比它大的数的左边,或者放到比它小的数的右边,这个东西就是二叉搜索树。
如果指定一个数,我们把比它小的一坨放到左边,比它大的一坨放右边,这个东西就叫做快速排序。
然后我们就开始码代码。js的动态性非常适合写树、图之类复杂数据结构的代码,我们不用像C++还要学习STL容器之类的,直接上手就干。
左小右大的二叉树

要分左右,最简单的结构就是二叉树。每个节点有左右两个子节点的引用:
class TreeNode {
constructor(key) {
this.key = key;
this.leftChild = null;
this.rightChild = null;
}
}
然后,根据小的放左边,大的放右边的原则,我们就可以写出一个插入节点的函数出来。
原理非常简单,如果比当前的节点的key值小,就看节点的左孩子节点是不是为空,如果为空,就new一个新节点成为当前节点的左孩子节点。
如果左孩子已经有了,那就递归,去跟左孩子节点去做对比。
如果大于当前节点的key,就去看右节点,过程与左节点一样。
function insertNode(node, key) {
if (key < node.key) {
if (node.leftChild === null) {
node.leftChild = new TreeNode(key);
} else {
insertNode(node.leftChild, key);
}
} else {
if (node.rightChild === null) {
node.rightChild = new TreeNode(key);
} else {
insertNode(node.rightChild, key);
}
}
}
树高千尺总要有根么,那么我们就给根节点建个数据结构:
class BinarySearchTree {
constructor() {
this.root = null;
}
insert(key) {
if (this.root === null) {
this.root = new TreeNode(key);
} else {
insertNode(this.root, key);
}
}
}
然后我们就可以往里面加新节点了:
let bst1 = new BinarySearchTree();
bst1.insert(1);
bst1.insert(2);
bst1.insert(4);
要做排序怎么排?先读左边的小的,再读中间的,最后读右边的。这就是中序遍历么。为了体现访问者设计模式,我们传入处理key的函数对象。
function walkTree(node, func) {
if (node === null) {
return;
}
if (node.leftChild !== null) {
walkTree(node.leftChild, func);
}
if (node.key !== null) {
func(node.key);
}
if (node.rightChild !== null) {
walkTree(node.rightChild, func);
}
}
我们再给树类封装个walk函数:
class BinarySearchTree {
constructor() {
this.root = null;
}
insert(key) {
if (this.root === null) {
this.root = new TreeNode(key);
} else {
insertNode(this.root, key);
}
}
walk(func) {
walkTree(this.root, func);
}
}
我们传个console.log,就可以打印出排序好的值了:
bst1.walk(console.log);
排序搞完了,我们还想加个搜索功能,看看在这棵二叉排序树中有没有这个元素。
这也不费事,比当前大就往左找,比当前小就往右找。
function searchNode(node, key) {
if (node === null || node.key === null) {
return null;
}
if (node.key === key) {
return key;
}
if (key < node.key) {
return searchNode(node.leftChild, key);
} else {
return searchNode(node.rightChild, key);
}
}
到此为止,完全不用看书,我们也写出来可以工作的二叉排序树了。
如果你学过数据结构课程,你会发现,这其中唯一复杂的二叉排序树的删除元素我没讲。因为暂时还用不上。但是不讲的好处,就是大家在节省脑力的情况下开心地学会了二叉排序树。
如果你学过删除二叉排序树节点并且觉得还容易理解的话,这里有个小提示,可能问题比你想象中的还复杂一点,以至于2009年《算法导论》出第3版的时候,更新了前两版中所用的,跟大多数书中用的删除算法。
快速排序
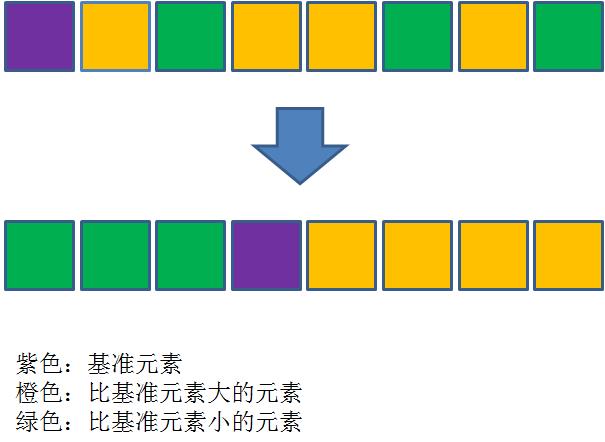
下面我们再来看左小右大按坨处理的方法,叫做快速排序。
我们先来个拆解大法,我们假设有个分堆函数叫做partition,我们传数组,起始位置和结束位置,它就把中间位置返回给我们。在中间位置之前的比中间值小,在中间位置之后的比中间值大。
于是快速排序就可以写成下面这样子,先分堆,然后针对左右两堆分别再去递归调用自身:
function qsort(list1, start, end) {
let middle = partition(list1, start, end);
if (middle - start > 1) {
qsort(list1, start, middle - 1);
}
if (end - middle > 1) {
qsort(list1, middle + 1, end);
}
}
下面我们就专心写partition函数。
怎么写?
原理还是,小的放左边,大的放右边。
最省事的方法自然是用个新的空数组放,小的从左放,大的从右放。
我们取一个值,比如最后一个数为中间数。然后从头开始比较每个数,如果比中间数大,就写到新数组的右边,然后右边指针向左移一格。如果比中间数小,就写到新数组的左边,然后左边指针向右移一格。
最后把新数组的值写回老数组,大功告成。
此时比起其它语言,js的优势就发挥出来了。新数组根本不用new,也不用算多长,用到哪个位置就直接写。
function partition(list1, start, end) {
//取最后一个值为比较基准
let middle_value = list1[end];
let list2 = [];
let left = start;
let right = end;
// end是中间数,所以不用作判断,最后写入即可
for (let i = start; i < end; i += 1) {
if (list1[i] > middle_value) {
list2[right] = list1[i];
right -= 1;
} else {
list2[left] = list1[i];
left += 1;
}
}
list2[left] = middle_value;
//将新数组结果复制到老数组里
for (let j = start; j <= end; j += 1) {
list1[j] = list2[j];
}
return left;
}
我们来写段代码测试下效果:
let list3 = [];
list3.push(3);
list3.push(100);
list3.push(8, 9, 10);
list3.push(13,12,7);
console.log(list3);
qsort(list3,0,list3.length-1);
console.log(list3);
输出如下:
[
3, 100, 8, 9,
10, 13, 12, 7
]
[
3, 7, 8, 9,
10, 12, 13, 100
]
更易读的版本:左右各用一个栈

上边的算法虽然更符合js的特点,但是Java等语言背景的同学看起来不太习惯。
我们可以写成更易理解的版本。
首先,partition函数后面要经常换版本,我们将其变成传入的参数:
function qsort2(list1, start, end, partition) {
let middle = partition(list1, start, end);
if (middle - start > 1) {
qsort(list1, start, middle - 1, partition);
}
if (end - middle > 1) {
qsort(list1, middle + 1, end, partition);
}
}
用一个数组看起来麻烦,那么我们搞两个:
let left = [];
let right = [];
for (let i = start; i < end; i += 1) {
if (list1[i] > middle_value) {
right.push(list1[i]);
} else {
left.push(list1[i]);
}
}
然后将两个数组以及中间值拼装在一起:
const list2 = left.concat(middle_value).concat(right);
完整的代码如下:
function partition1(list1, start, end) {
//取最后一个值为比较基准
let middle_value = list1[end];
let left = [];
let right = [];
for (let i = start; i < end; i += 1) {
if (list1[i] > middle_value) {
right.push(list1[i]);
} else {
left.push(list1[i]);
}
}
const len = left.length;
const list2 = left.concat(middle_value).concat(right);
for (let j = start; j <= end; j += 1) {
list1[j] = list2[j-start];
}
return start+len;
}
快速排序的第一次进化:错配的互换下
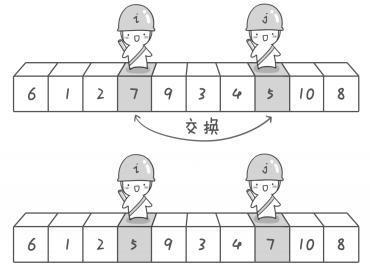
学会了快速排序之后,我们继续反思基本原理:小的放左边,大的放右边。
如果我们在左边数能找到一个大的,那么右边一定有一个小的放错堆的。我们把这两个一交换,就向完成前进了一步。
当然,如果左边找不到,右边也没有,那就是已经完成了。
所以这个问题拆解成这样:
- 先从左往右找比中间值大的。如果一直找到右界还没找到,就说明已经partition成功了。
- 如果找到了,记下来位置。再从右边开始往左找,直到找到一个不小于中间值的,再记下来。
- 交换刚才两个值的位置。交换完之后,交换的后的小值的左边,以及大值的右边都是好的。
- 现在以刚才交换后的小值的右边为左界,大值的右边为右界,重复第一步的判断。
我们大致写成这样:
while (left < right) {
while (list1[left] <= middle_value && left < right) {
left += 1;
}
while (list1[right] > middle_value && right > left) {
right -= 1;
}
if (left === right) {
break;
} else {
swap(list1, left, right);
}
}
现在我们又体会到将parition函数从qsort中拆解出来的好处,我们只需要把partition函数替换成新算法就可以了,qsort完全不需要改动。
我们现在就可以写partition的第2版了:
function partition2(list1, start, end) {
//取最后一个值为比较基准
let middle_value = list1[end];
let left = start;
let right = end;
while (left < right) {
while (list1[left] <= middle_value && left < right) {
left += 1;
}
while (list1[right] > middle_value && right > left) {
right -= 1;
}
if (left === right) {
break;
} else {
swap(list1, left, right);
}
}
return left;
}
其中,swap用于交换数组中的两个元素:
function swap(list1, pos1, pos2) {
let tmp = list1[pos1];
list1[pos1] = list1[pos2];
list1[pos2] = tmp;
}
写个用例简单测一下:
let list3 = [];
list3.push(3);
list3.push(100);
list3.push(8, 9, 10);
list3.push(13, 12, 7);
list3.push(25, 26, 27);
console.log(list3);
qsort2(list3, 0, list3.length - 1, partition2);
console.log(list3);
输出如下:
[
3, 100, 8, 9, 10,
13, 12, 7, 25, 26,
27
]
[
3, 7, 8, 9, 10,
12, 13, 25, 26, 27,
100
]
这一版比起上一版是要复杂一点了,毕竟这是图灵奖得主托尼-霍尔爵士发明的,写的时候可以多写几个用例测一测。但是这个思想还是容易理解的。
我们给qsort2加一行日志,打印出partition返回的中值在哪里。
function qsort2(list1, start, end, partition) {
let middle = partition(list1, start, end);
console.log(`start=${start},middle=${middle},end=${end}`);
if (middle - start > 1) {
qsort2(list1, start, middle - 1, partition);
}
if (end - middle > 0) {
qsort2(list1, middle, end, partition);
}
}
我们从最简单的两个元素的开始看:
list8 = [7,3];
qsort2(list8, 0, list8.length - 1, partition2);
console.log(list8);
输出如下:
start=0,middle=1,end=1
[ 3, 7 ]
中值是1,也就是说比1大的在2之后,小于等于1的,是0和1。
这样如果看起来还不清晰的话,我们可以把第一次partition2的原始值和划分后的结果打印出来,这样就更一目了然了:
function partition2(list1, start, end) {
console.log(`before partition ${list1.slice(start,end+1)}`);
//取最后一个值为比较基准
let middle_value = list1[end];
let left = start;
let right = end;
while (left < right) {
while (list1[left] <= middle_value && left < right) {
left += 1;
}
while (list1[right] > middle_value && right > left) {
right -= 1;
}
if (left === right) {
break;
} else {
swap(list1, left, right);
}
}
console.log(`after partition ${list1.slice(start,end+1)}`);
return left;
}
我们再看上面的2个元素的最小例子:
list8 = [7,3];
qsort2(list8, 0, list8.length - 1, partition2);
console.log(list8);
输出为:
before partition 7,3
after partition 3,7
[ 3, 7 ]
说明总共划分了一次,从[7,3]变成了[3,7].
我们再复杂一点,来个三个元素的:
list7 = [3, 7