算法 ——插入排序（直接插入排序，希尔排序）的基本思想和解析

Posted 2021-10-17 努力学习的少年

1.插入排序

插入排序的基本思想：

插入排序是一种最简单的的排序思想，它的思想是将一个数据插入到一个有序的数据列表，得到一个新的有序列表。

 插入排序类型于将我们完的扑克，将牌一张一张插入到我们的序列中，形成一个有序的序列。

 

 整形数组 9  1  2  5  7 4插入排序的过程。蓝色箭头指向的值为tmp值。紫色箭头是tmp插入的位置。

 

 

 

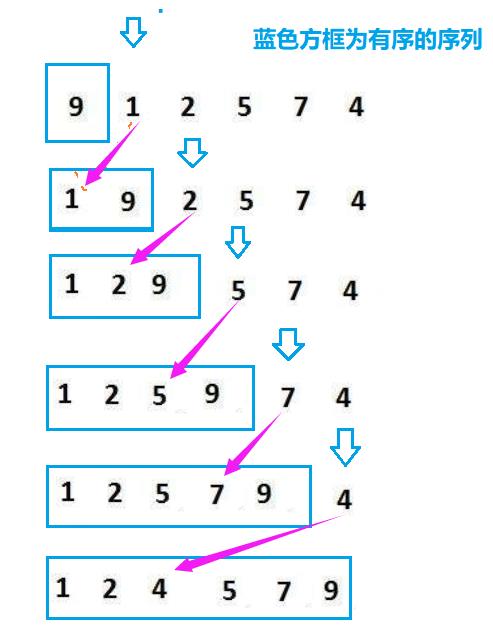
       插入排序 对应的代码：

void Insert(int arr[], int n)
{
	for (int i = 0; i < n; i++)//进行插入排序的次数
	{
		int end = i;//指向有序序列结尾的指针
		int tmp = arr[end];//蓝色箭头指向的值
		while (end - 1 >= 0 && arr[end - 1] > tmp)
		{
			arr[end] = arr[end - 1];//将数据后移
			end--;
		}
		arr[end] = tmp;//将数据插入到正确的位置上
	}
}

 插入排序的时间复杂度：

当一个序列是完全有序的时候，例如序列为1  2  3  4  5 .....，那么只需遍历一遍序列， 此时的插入排序时间复杂度为O(N)，所以当序列越接近有序的时候，时间复杂度就越接近O(N)；如果一个序列是完全逆序的时候，例如序列 5 4 3 2 1 .....,那么每次遍历的时候都需要将数据插入到前面时间复杂度为O(N^2），但由于时间复杂度是按最坏的情况去考虑的，所以插入排序的时间复杂度为O(N^2).

 2.希尔排序

   希尔排序又称“缩小增量排序”，它也是一种插入排序的方法，但在时间效率比直接插入排序要好很多。

它的基本思想是：先将整个待排序列分成若干子序列分别进行直接插入排序，待整个序列中记录”基本有序时“在对整个序列进行一次直接插入排序。

我们以数组中 9  1  2  5  7   4  8  6  3  5来看一下希尔排序是怎样的把这个数组排成一个有序的。

 

 

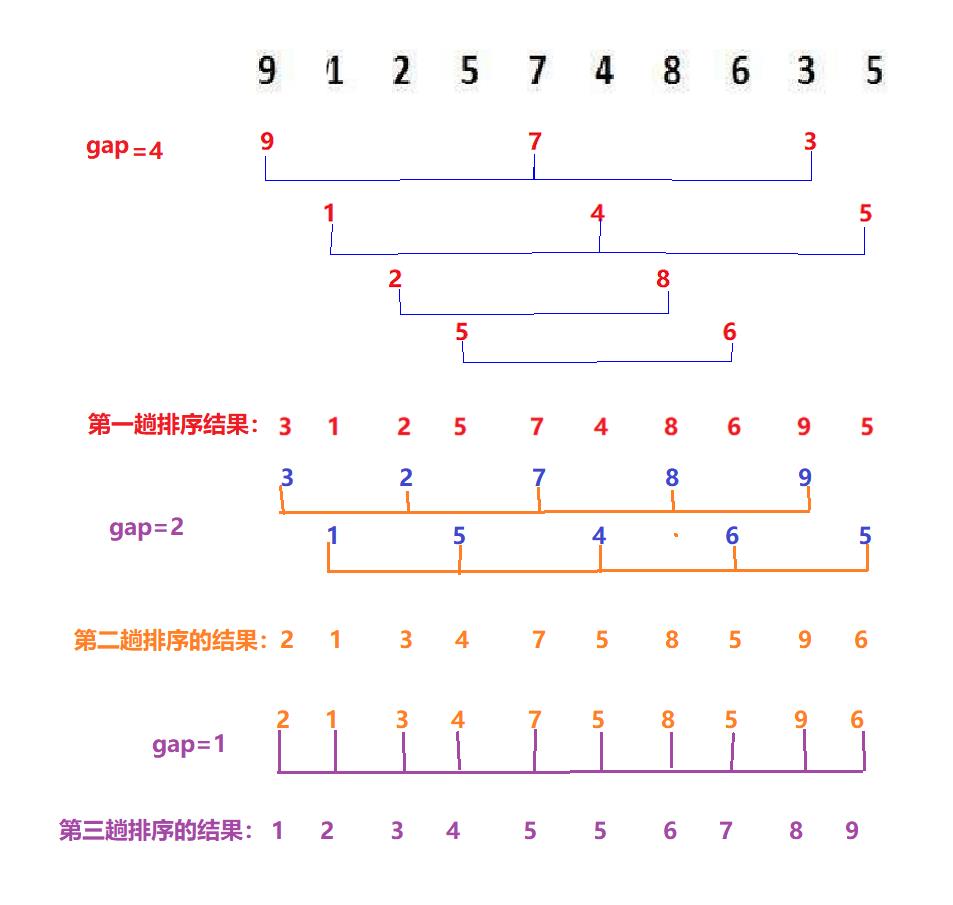
 其中的gap为每一趟中的子序列之间的间隔，对每一个子序列进行插入排序，当一趟排序完成后，就进行下一趟排序，gap就不断缩小，则序列也不断的接近有序，当gap减到为1时并且排序完成后则整个序列就为有序的。当gap很大时，则序列就排序的很快，当gap很小时，则排出的序列就接近有序。当gap为1时相当于插入排序，此时序列已经接近有序了，所以该插入排序的时间复杂度接近O(n). 

插入排序的代码：

//希尔排序
void ShellSort(int arr[], int n)
{
	  int gap = n ;//gap为个子序列的间隔
	  while (gap > 1)
	  {
		  gap = gap / 3 + 1;//不断缩小gap
	 
	 for (int i = 0; i < n - gap; i++)//进行每一趟的排序
	 {
		 int end = i;//每一趟中子序列的插入排序
		 //对子序列中数据进行插入排序
		 int tmp = arr[end + gap];
		 while (end >= 0 && arr[end] > tmp)
		 {
		    arr[end + gap] = arr[end];
			end -= gap;
		 }
	    arr[end + gap] = tmp;
	 }
	}
 }

希尔排序代码解析：

1.gap=gap/3+1,

每一趟的gap都不断缩小3倍，加上1是防止最后一趟的gap为0，因为最后第二趟gap为2时，则最后一趟除3为2/3就为0；

2.

         int end = i;
         int tmp = arr[end + gap];
         while (end >= 0 && arr[end] > tmp)
         {
            arr[end + gap] = arr[end];
            end -= gap;
         }
        arr[end + gap] = tmp;

为每一趟中的子序列的插入排序，子序列中的间隔为gap，移动都是往后挪动gap的位置。

对应下面子序列的插入过程。类型插入排序，只是每个数据的间隔变为gap。插入排序的gap为

 

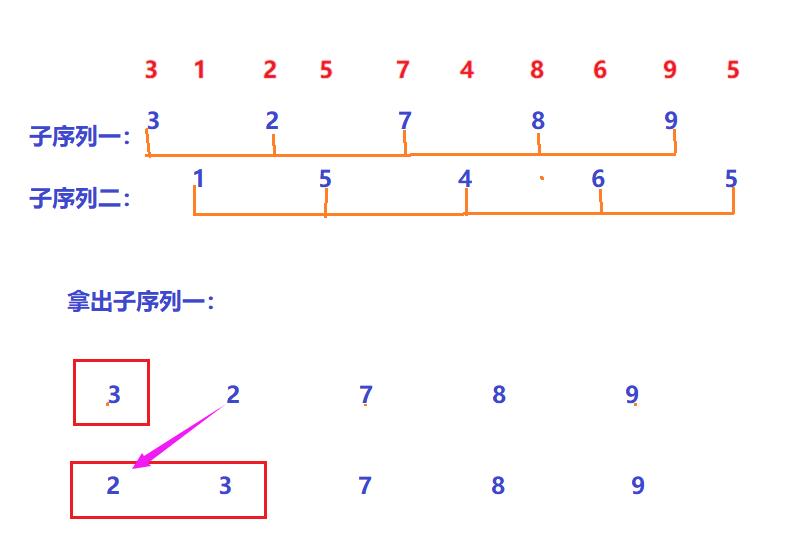
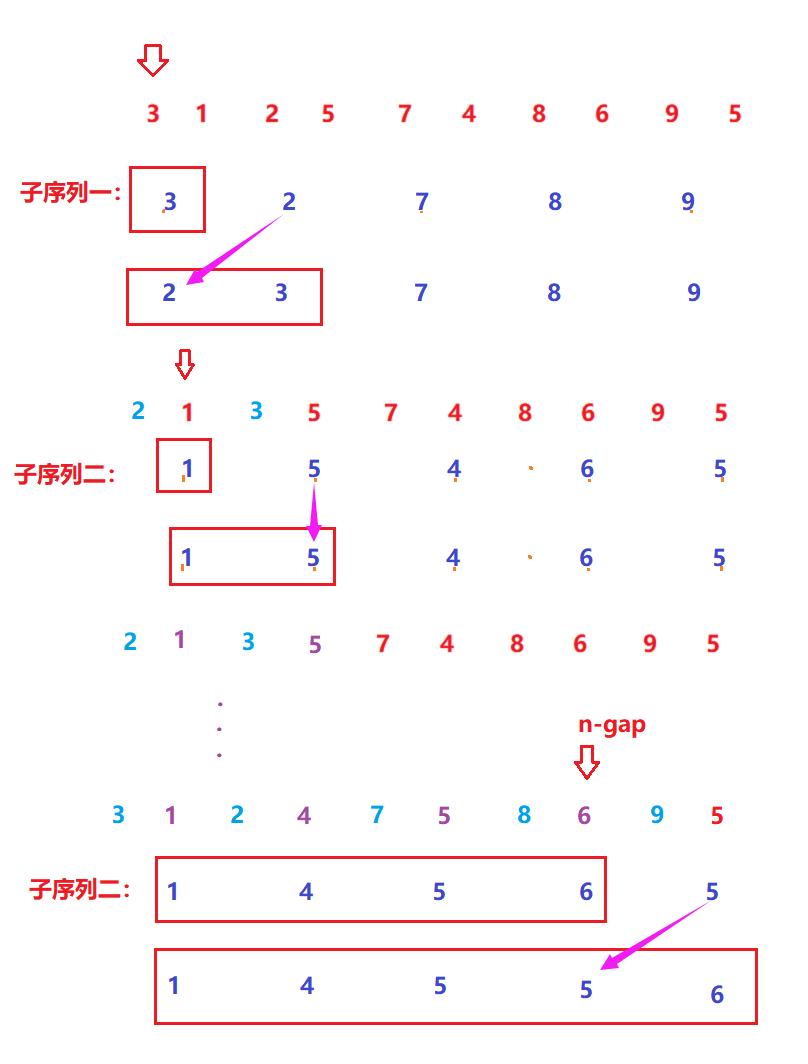
 3.for (int i = 0; i < n - gap; i++)

因为我们要对每个子序列中进行插入排序，使每个子序列都有序，这时我们遍历整个序列，当i指向哪一个值后，我们就浮现i相对应的子序列，在子序列中，我们将i后一位的值插入到有序的子序列中，当i到排n-gap后就终止。如下图所示。

 希尔排序的时间复杂度：

希尔排序中的分析是一个复杂的问题。因为它的时间复杂度是所取”增量“序列的函数，这涉及一些数学上尚未研究的难题，到目前为止尚未有人求得一种最好的增量序列，但大量的研究已经推出它的时间复杂度为O(n^(3/2) )

我们可以大概计算希尔排序最坏的时间复杂度：

先算for循环的时间复杂度，

当gap很大的时候，里面的while循环几乎不计为，所以for循环为O（N),

.......

当gap越来越小时，本来是插入排序的，但由于序列中已经接近有序，所以插入排序接近O（N）

再算 while (gap > 1)的时间复杂度

n/3/3/3/3...=1

3^x=n ,x是循环的次数，所以while的时间复杂度为O(log3 n)

所以希尔排序的最坏的时间复杂度大概是O(( log3 n) *n),相较于插入排序，这个算法算快的。