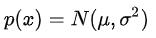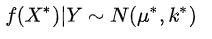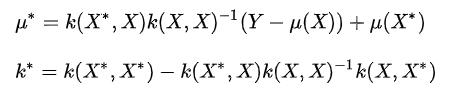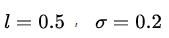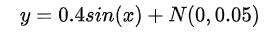机器学习笔记：高斯过程

Posted 2021-10-17 UQI-LIUWJ

1 高斯分布回顾

一维高斯分布 

        当维度上升到多维的时候（比如有限的p维），我们称之为高维高斯分布，记作：

        其中 μ是p维向量，表示每个维度的均值，Σ的第（i，j）项表示第i个维度和第j个维度之间的协方差

2 高斯过程

高斯过程可以看成是定义在连续域上的无限维高斯分布

用符号表示，有：

 2.1 高斯过程举例

以下图为例，假设横轴表示时间，纵轴表示体能值。

假设对于某一个物种而言，在任何时刻，体能值都满足正态分布（只不过不同的时间点，分布的均值和方差可能不同）

 

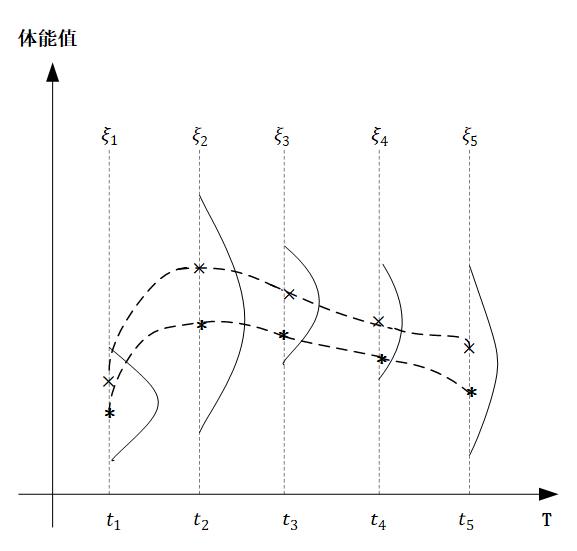
        我们在图中选取了5个点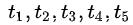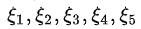，对应5个时刻的体能值，分别满足高斯分布

        不失一般性，我们有：任取一个时刻t，

        而图中的两条虚线是两个高斯过程的样本。也即我们取遍所有时刻的t，获得的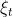连成的一条虚线 

 2.2 形式化语言描述高斯过程

我们和p维的高斯分布进行类比：

	p维高斯分布	高斯过程（无限维高斯分布）
均值		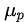关于时刻t的函数，m(t)
方差		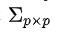核函数（协方差函数）k(s,t)，其中s和t分别代表任意两个时刻
表示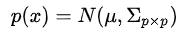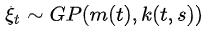

 2.3 径向基函数（RBF）

这是一种较为常见的核函数

 

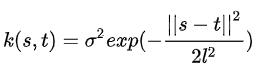
•  这里的σ和l是径向基函数的超参数，是可以提前设置好的

• s和t表示高斯过程连续域上的两个不同的时间点，两个点距离越大，两个分布之间的协方差值越小，相关性越小

2.3.1RBF代码

import numpy as np
def rbf(x):
    sigma=1
    l=1
    #设置两个rbf的超参数
    
    m=x.shape[0]

    k=np.zeros((m,m))
#初始化这个数据的径向基矩阵
    
    for i in range(m):
        for j in range(m):
            k[i][j]=np.exp(-np.sum((x[i]-x[j])**2)/2)
#这里为什么要sum呢？因为我某一个时刻，特征可能不止一个维度（就像这里我们每个时刻是两个维度）
    return(k)

a=np.array([[1,2],
           [3,4],
           [5,6]])

#三个时刻的数据，每个时刻有两维特征

rbf(a)
'''
array([[1.00000000e+00, 1.83156389e-02, 1.12535175e-07],
       [1.83156389e-02, 1.00000000e+00, 1.83156389e-02],
       [1.12535175e-07, 1.83156389e-02, 1.00000000e+00]])
'''
#这相当于一个3*3的协方差矩阵

3 高斯过程回归

这个过程可以看成先验概率+观测值——>后验概率的过程

先验概率：通过μ(t)和k(s,t)定义一个高斯过程

3.1 高维高斯分布的条件概率

高斯分布的联合概率，边缘概率和条件概率都仍然满足高斯分布

假设n维随机变量满足：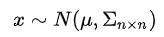

如果我们把这n维的随机变量分成两部分：p维的xa和q维的xb，（q+p=n），那么我们有：

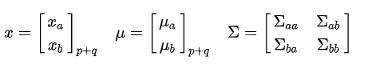
 其中 ,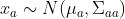

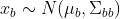
同时，条件概率也是高维高斯分布

 3.2 类比到高斯过程回归

        我们将均值向量换成均值函数，把协方差矩阵换成核函数，把高维高斯分布看成高斯过程（无限维高斯分布）

假设我们有观测值（X,Y），于是我们记其他的非观测点是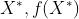

首先，联合分布是满足无限维高斯分布的

 与此同时，条件概率也满足无限维高斯分布（高斯过程）

类比前面的，我们现在有：

 

 

 3.3高斯过程实例

 下面我们来实际的进行代码演示

令：

【注：这里的μ(X)是Y的分布的均值，不是X的分布均值 】

中的 

 取四个观测值 X=[1,3,7,9] ，Y为

 我们在四个观测点的基础上，来求高斯过程的后验。

 在下面的具体程序实现中，由于绘图是离散化处理的，因此连续域上的均值函数以及核函数，我们使用一个 很大的 n 维均值向量以及n×n  协方差矩阵进行表示

 3.3.1 代码部分

import numpy as np
import matplotlib.pyplot as plt
def rbf(x,y,l=0.5,simga=0.2):
    sigma=1
    l=1
    #设置两个rbf的超参数
    
    m=x.shape[0]
    n=y.shape[0]

    k=np.zeros((m,n), dtype=float)
    #初始化这个数据的径向基矩阵
    
    for i in range(m):
        for j in range(n):
            k[i][j]=np.exp(-np.sum((x[i]-y[j])**2)/(2*l**2))*simga**2
            #这里为什么要sum呢？因为我某一个时刻，特征可能不止一个维度（就像这里我们每个时刻是两个维度）
    return(k)

def getY(x):
    #生成观测值对应的Y
    Y=np.sin(x)*0.4+np.random.normal(0,0.05,size=x.shape)
    return(Y)

def guassian_process(X,X_star):
    K_XX=rbf(X,X)#f(X,X)
    K_XX_=rbf(X,X_star)#f(X,X*)
    K_X_X=rbf(X_star,X)#f(X*,X)
    K_X_X_=rbf(X_star,X_star)#f(X*,X*)
    
    K_XX_inv=np.linalg.inv(K_XX+ 1e-8 * np.eye(len(X)))
    #f(X,X)的逆，加后一项是为了防止不可逆
    
    mu_star=K_X_X.dot(K_XX_inv).dot(Y-0)+0
    #μ*  后面的μ(X*)也是0，是因为整体的μ(X)是0，去掉那几个点之后的μ(X*)也是0
    
    cov_star=K_X_X_-K_X_X.dot(K_XX_inv).dot(K_XX_)
    #Σ*
    
    return(mu_star,cov_star)

#根据观察点X，修正生成高斯过程新的均值和协方差


f,ax=plt.subplots(2, 1,
                  figsize=(10,10), 
                  sharex=True,
                  sharey=True)
#绘制高斯过程的先验 （μ(x)=0)
X_pre = np.arange(0, 10, 0.1)
Y_pre = np.array([0]*len(X_pre))

conv_pre=rbf(X_pre,X_pre)

uncertainty=1.96*np.sqrt(np.diag(conv_pre))
#1.96是高斯分布的95%置信区间，这里表示每个点对应的95%置信区间

ax[0].fill_between(
    X_pre,
    Y_pre+uncertainty,
    Y_pre-uncertainty,
    alpha=0.2)

ax[0].plot(X_pre,Y_pre,label="pre_expectation")
ax[0].legend()
#ax[0]绘制的是完全没有任何观测点的时候的先验概率分布，我们只知道μ(X)=0

X=np.array([1,3,7,9])
Y=getY(X)
#我们观测到了这四个点，其他的点μ(x)依旧为0
X_star=np.arange(0,10,0.1)
Y_star,conv_star=guassian_process(X,X_star)#得到 f(x*)|Y的均值和方差
uncertainty_star=1.96*np.sqrt(np.diag(conv_star))
ax[1].fill_between(
    X_star,
    Y_star+uncertainty_star,
    Y_star-uncertainty_star,
    alpha=0.2)
ax[1].plot(X_star,Y_star,label="after_expectation")
ax[1].scatter(X,Y,c='green')
ax[1].legend()
#ax[1]绘制的是有四个观测点之后的后验概率分布

 3.3.2 结论部分

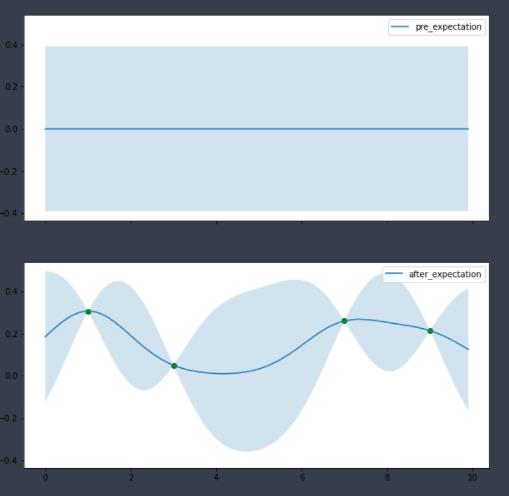
         ax[0]绘制的是完全没有任何观测点的时候的先验概率分布，我们只知道μ(X)=0；ax[1]绘制的是有四个观测点之后的后验概率分布。

        明显可以看出，由于观测点信息的带入，连续域上各个点的均值发生了变化。同时大部分取值点的  置信空间也收窄，证明确定性得到了增强。

 参考内容：如何通俗易懂地介绍 Gaussian Process？ - 知乎 (zhihu.com)

4 sklearn 

sklearn 笔记：高斯过程_UQI-LIUWJ的博客-CSDN博客