深度学习基础:1.张量的基本操作
Posted Z|Star
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习基础:1.张量的基本操作相关的知识,希望对你有一定的参考价值。
本篇博文是对pytorch框架下张量操作的内容汇总,为方便查看,已设置目录,查阅时可快速跳转。编程工具使用的是jupyter,黑框部分为代码,白框部分为运行结果。
内容速览
张量(Tensor)的基本含义
张量,可以简单的理解为多维数组,是二维向量在更高的维度的延申。
用到的库和框架
import torch
import numpy as np
张量的创建
通过列表创建张量
# 通过列表创建张量
t = torch.tensor([1, 2])
t
tensor([1, 2])
通过元组创建张量
# 通过元组创建张量
torch.tensor((1, 2))
tensor([1, 2])
将numpy创建的数组转换成张量
a = np.array((1, 2))
t1 = torch.tensor(a)
t1
tensor([1, 2], dtype=torch.int32)
注:张量默认创建int64(长整型)类型,整数型的数组默认创建int32(整型)类型。
二维数组的创建
# 用list的list创建二维数组
t2 = torch.tensor([[1, 2], [3, 4]])
t2
tensor([[1, 2],
[3, 4]])
张量的类型
查看变量的类型
t.dtype
torch.int64
注:创建浮点型数组时,张量默认是float32(单精度浮点型),而Array则是默认float64(双精度浮点型)。
| 数据类型 | dtype |
|---|---|
| 32bit浮点数 | torch.float32或torch.float |
| 64bit浮点数 | torch.float64或torch.double |
| 16bit浮点数 | torch.float16或torch.half |
| 8bit无符号整数 | torch.unit8 |
| 8bit有符号整数 | torch.int8 |
| 16bit有符号整数 | torch.int16或torch.short |
| 16bit有符号整数 | torch.int16或torch.short |
| 32bit有符号整数 | torch.int32或torch.int |
| 64bit有符号整数 | torch.int64或torch.long |
| 布尔型 | torch.bool |
| 复数型 | torch.complex64 |
创建固定类型的张量
# 创建int16整型张量
torch.tensor([1.1, 2.7], dtype = torch.int16)
tensor([1, 2], dtype=torch.int16)
张量类型的转化
张量类型的隐式转化
创建张量时,同时包含整数和浮点数,张量类型会变成浮点数;同时包含布尔型和整数型,张量类型会变成整数型。
张量类型的隐式转化
转化为默认浮点型(32位)
# 转化为默认浮点型(32位)
t.float()
转化为双精度浮点型
# 转化为双精度浮点型
t.double()
转化为16位整数
# 转化为16位整数
t.short()
张量的维度
创建高维张量
查看张量的维度ndim
# 使用ndim属性查看张量的维度
t1.ndim
查看形状shape/size
# 使用shape查看形状
t1.shape
# 使用size查看形状
t1.size()
查看拥有几个(N-1)维元素numel
# 返回总共拥有几个数
t1.numel()
创建零维张量
有一类特殊的张量,被称为零维张量。该类型张量只包含一个元素,但又不是单独一个数。
将零维张量视为拥有张量属性的单独一个数。例如,张量可以存在GPU上,但Python原生的数值型对象不行,但零维张量可以,尽管是零维。
t = torch.tensor(1)
t
tensor(1)
张量的形变
flatten拉平:将任意维度张量转化为一维张量
t.flatten()
tensor([1, 2, 3, 4])
注:如果将零维张量使用flatten,则会将其转化为一维张量。
reshape方法:任意变形
t1
tensor([1, 2])
# 转化为两行、一列的向量
t1.reshape(2, 1)
tensor([[1],
[2]])
特殊张量的创建
全0张量zeros
torch.zeros([2, 3]) # 创建全是0的,两行、三列的张量(矩阵)
tensor([[0., 0., 0.],
[0., 0., 0.]])
全1张量ones
torch.ones([2, 3])
tensor([[1., 1., 1.],
[1., 1., 1.]])
单位矩阵eye
torch.eye(5)
tensor([[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]])
对角矩阵diag
略有特殊的是,在PyTorch中,需要利用一维张量去创建对角矩阵。
t1
tensor([1, 2])
torch.diag(t1)
tensor([[1, 0],
[0, 2]])
服从0-1均匀分布的张量rand
torch.rand(2, 3)
tensor([[0.9223, 0.9948, 0.2804],
[0.8130, 0.2890, 0.5319]])
服从标准正态分布的张量randn
torch.randn(2, 3)
tensor([[-1.2513, 0.6465, -2.3011],
[ 0.8447, 1.6856, 1.3615]])
服从指定正态分布的张量normal
torch.normal(2, 3, size = (2, 2)) # 均值为2,标准差为3的张量
tensor([[2.4660, 1.4952],
[6.0202, 0.7525]])
整数随机采样结果randint
torch.randint(1, 10, [2, 4]) # 在1-10之间随机抽取整数,组成两行四列的矩阵
tensor([[5, 8, 8, 3],
[6, 1, 4, 2]])
生成数列arange/linspace
torch.arange(5) # 和range相同
tensor([0, 1, 2, 3, 4])
torch.arange(1, 5, 0.5) # 从1到5(左闭右开),每隔0.5取值一个
tensor([1.0000, 1.5000, 2.0000, 2.5000, 3.0000, 3.5000, 4.0000, 4.5000])
torch.linspace(1, 5, 3) # 从1到5(左右都包含),等距取三个数
tensor([1., 3., 5.])
生成未初始化的指定形状矩阵empty
torch.empty(2, 3)
tensor([[0.0000e+00, 1.7740e+28, 1.8754e+28],
[1.0396e-05, 1.0742e-05, 1.0187e-11]])
根据指定形状,填充指定数值full
torch.full([2, 4], 2)
tensor([[2, 2, 2, 2],
[2, 2, 2, 2]])
张量(Tensor)和其他相关类型之间的转化方法
张量转化为数组numpy
t1.numpy()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=int64)
张量转化为列表tolist
t1.tolist()
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
张量转化为数值item
n.item()
1
张量的拷贝
张量的浅拷贝
创建张量t1,若运行t2=t1,则是张量的浅拷贝,两者指向同一块内存空间,第一个改变另一个也改变。
张量的深拷贝clone
张量的深拷贝指的是两者独立开来,互不影响。
t2 = t1.clone()
t1
tensor([ 1, 10, 3, 4, 5, 6, 7, 8, 9, 10])
t2
tensor([ 1, 10, 3, 4, 5, 6, 7, 8, 9, 10])
此时修改t1,t2不会发生变化。
张量的索引
张量的符号索引
张量的符号索引指的是类似数组的方式去索引张量。
一维张量索引
t1 = torch.arange(1, 11)
t1
tensor([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
t1[0]
tensor(1)
注:张量索引出来的结果还是零维张量, 而不是单独的数。要转化成单独的数,需要使用item()方法。
t1[: 8: 2] # 从第一个元素开始索引到第9个元素(不包含),并且每隔两个数取一个
tensor([1, 3, 5, 7])
二维张量索引
二维张量的索引逻辑和一维张量的索引逻辑基本相同,二维张量可以视为两个一维张量组合而成,而在实际的索引过程中,需要用逗号进行分隔,分别表示对哪个一维张量进行索引、以及具体的一维张量的索引。
t2 = torch.arange(1, 10).reshape(3, 3)
t2
tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
t2[0, ::2] # 表示索引第一行、每隔两个元素取一个
tensor([1, 3])
注:“:“左右两边为空代表全取。
三维张量索引
在二维张量索引的基础上,三维张量拥有三个索引的维度。我们将三维张量视作矩阵组成的序列,则在实际索引过程中拥有三个维度,分别是索引矩阵、索引矩阵的行、索引矩阵的列。
t3 = torch.arange(1, 28).reshape(3, 3, 3)
t3
tensor([[[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9]],
[[10, 11, 12],
[13, 14, 15],
[16, 17, 18]],
[[19, 20, 21],
[22, 23, 24],
[25, 26, 27]]])
t3.shape
torch.Size([3, 3, 3])
t3[:: 2, :: 2, :: 2] # 每隔两个取一个矩阵,对于每个矩阵来说,行和列都是每隔两个取一个
tensor([[[ 1, 3],
[ 7, 9]],
[[19, 21],
[25, 27]]])
本质上,索引完全围绕张量的形状(shape),三个索引值分别对应shape的三个维度量。
张量的函数索引
在PyTorch中,我们还可以使用index_select函数,通过指定index来对张量进行索引。
t1
tensor([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
indices = torch.tensor([1, 2])
indices
tensor([1, 2])
torch.index_select(t1, 0, indices)
tensor([2, 3])
在index_select函数中,第二个参数实际上代表的是索引的维度。对于t1这个一维向量来说,由于只有一个维度,因此第二个参数取值为0,就代表在第一个维度上进行索引。
视图view
该方法会返回一个类似视图的结果,该结果和原张量对象共享一块数据存储空间。和mysql的视图概念类似。
t = torch.arange(6).reshape(2, 3)
t
tensor([[0, 1, 2],
[3, 4, 5]])
te = t.view(3, 2) # 构建一个数据相同,但形状不同的“视图”
te
tensor([[0, 1],
[2, 3],
[4, 5]])
张量的分片函数
分块:chunk函数
chunk函数能够按照某维度,对张量进行均匀切分,并且返回结果是原张量的视图。
t2 = torch.arange(12).reshape(4, 3)
t2
tensor([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]])
tc = torch.chunk(t2, 4, dim=0) # 在第零个维度上(按行),进行四等分
tc
(tensor([[0, 1, 2]]),
tensor([[3, 4, 5]]),
tensor([[6, 7, 8]]),
tensor([[ 9, 10, 11]]))
拆分:split函数
split既能进行均分,也能进行自定义切分。当然,需要注意的是,和chunk函数一样,split返回结果也是view。
t2 = torch.arange(12).reshape(4, 3)
t2
tensor([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]])
torch.split(t2, 2, 0) # 第二个参数只输入一个数值时表示均分,第三个参数表示切分的维度
(tensor([[0, 1, 2],
[3, 4, 5]]),
tensor([[ 6, 7, 8],
[ 9, 10, 11]]))
torch.split(t2, [1, 3], 0) # 第二个参数输入一个序列时,表示按照序列数值进行切分,也就是1/3分
(tensor([[0, 1, 2]]),
tensor([[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]]))
张量的合并操作
拼接函数:cat
cat函数可以实现张量的拼接。
a = torch.zeros(2, 3)
a
tensor([[0., 0., 0.],
[0., 0., 0.]])
b = torch.ones(2, 3)
b
tensor([[1., 1., 1.],
[1., 1., 1.]])
torch.cat([a, b]) # 按照行进行拼接,dim默认取值为0
tensor([[0., 0., 0.],
[0., 0., 0.],
[1., 1., 1.],
[1., 1., 1.]])
堆叠函数:stack
和拼接不同,堆叠不是将元素拆分重装,而是简单的将各参与堆叠的对象分装到一个更高维度的张量里,参与堆叠的张量必须形状完全相同。
a
tensor([[0., 0., 0.],
[0., 0., 0.]])
b
tensor([[1., 1., 1.],
[1., 1., 1.]])
torch.stack([a, b]) # 堆叠之后,生成一个三维张量
tensor([[[0., 0., 0.],
[0., 0., 0.]],
[[1., 1., 1.],
[1., 1., 1.]]])
张量维度变换
通过reshape方法,能够灵活调整张量的形状。而在实际操作张量进行计算时,往往需要另外进行降维和升维的操作,当我们需要除去不必要的维度时,可以使用squeeze函数,而需要手动升维时,则可采用unsqueeze函数。
squeeze函数:删除不必要的维度
t1 = torch.zeros(1, 1, 3, 2, 1, 2)
t1.shape
torch.Size([1, 1, 3, 2, 1, 2])
torch.squeeze(t1)
tensor([[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]]])
torch.squeeze(t1).shape
torch.Size([3, 2, 2])
注:squeeze相当于剔除了原shape中的大小为1的维度。
unsqeeze函数:手动升维
t = torch.zeros(1, 2, 1, 2)
t.shape
torch.Size([1, 2, 1, 2])
torch.unsqueeze(t, dim = 0) # 在第1个维度索引上升高1个维度
tensor([[[[[0., 0.]],
[[0., 0.]]]]])
torch.unsqueeze(t, dim = 0).shape
torch.Size([1, 1, 2, 1, 2])
注:unsqueeze相当于在dim维度之前增加了大小为1的维度。
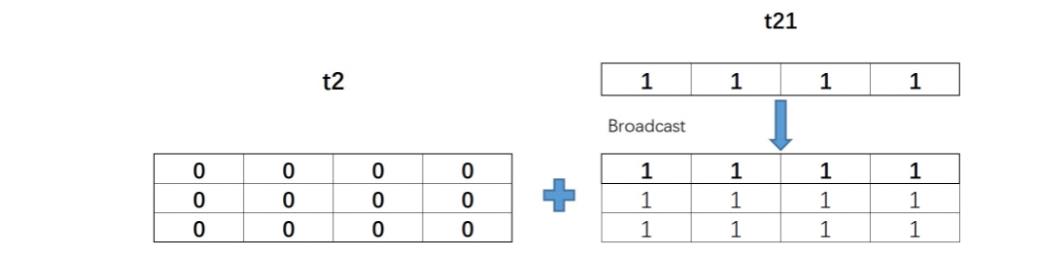
张量的广播
广播,简单理解,当两个张量维度不同或形状不同时进行计算时,维度小的张量会自动复制自己维度为1的数值,从而顺利实现计算。
t2
tensor([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
t2.shape
torch.Size([3, 4])
t21 = torch.ones(1, 4)
t21
tensor([[1., 1., 1., 1.]])
t21的形状是(1, 4),和t2的形状(3, 4)在第一个分量上取值不同,但该分量上t21取值为1,因此可以广播,也就可以进行计算
t21 + t2
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
t21和t2的实际计算过程如下:
基本数学运算
| 函数 | 描述 |
|---|---|
| torch.add(t1,t2 ) | t1、t2两个张量逐个元素相加,等效于t1+t2 |
| torch.subtract(t1,t2) | t1、t2两个张量逐个元素相减,等效于t1-t2 |
| torch.multiply(t1,t2) | t1、t2两个张量逐个元素相乘,等效于t1*t2 |
| torch.divide(t1,t2) | t1、t2两个张量逐个元素相除,等效于t1/t2 |
不常用,常用加减乘除等效形式。
数值调整函数
| 函数 | 描述 |
|---|---|
| torch.abs(t) | 返回绝对值 |
| torch.ceil(t) | 向上取整 |
| torch.floor(t) | 向下取整 |
| torch.round(t) | 四舍五入取整 |
| torch.neg(t) | 返回相反的数 |
常用科学计算
| 数学运算函数 | 数学公式 | 描述 |
|---|---|---|
| 幂运算 | ||
| torch.exp(t) | $ y_{i} = e^{x_{i}} $ | 返回以e为底、t中元素为幂的张量 |
| torch.expm1(t) | $ y_{i} = e^{x_{i}} $ - 1 | 对张量中的所有元素计算exp(x) - 1 |
| torch.exp2(t) | $ y_{i} = 2^{x_{i}} $ | 逐个元素计算2的t次方。 |
| torch.pow(t,n) | $\\text{out}_i = x_i ^ \\text{exponent} $ | 返回t的n次幂 |
| torch.sqrt(t) | $ \\text{out}{i} = \\sqrt{\\text{input}{i}} $ | 返回t的平方根 |
| torch.square(t) | $ \\text{out}_i = x_i ^ \\text{2} $ | 返回输入的元素平方。 |
| 对数运算 | ||
| torch.log10(t) | $ y_{i} = \\log_{10} (x_{i}) $ | 返回以10为底的t的对数 |
| torch.log(t) | $ y_{i} = \\log_{e} (x_{i}) $ | 返回以e为底的t的对数 |
| torch.log2(t) | $ y_{i} = \\log_{2} (x_{i}) $ | 返回以2为底的t的对数 |
| torch.log1p(t) | $ y_i = \\log_{e} (x_i $ + 1) | 返回一个加自然对数的输入数组。 |
| 三角函数运算 | ||
| torch.sin(t) | 三角正弦。 | |
| torch.cos(t) | 元素余弦。 | |
| torch.tan(t) | 逐元素计算切线。 |
排序运算:sort
排序和python原始库差不多。
升序
# 升序排列
torch.sort(t)
降序
# 降序排列
torch.sort(t, descending=True)
统计分析函数
| 函数 | 描述 |
|---|---|
| torch.mean(t) | 返回张量均值 |
| torch.var(t) | 返回张量方差 |
| torch.std(t) | 返回张量标准差 |
| torch.var_mean(t) | 返回张量方差和均值 |
| torch.std_mean(t) | 返回张量标准差和均值 |
| torch.max(t) | 返回张量最大值 |
| torch.argmax(t) | 返回张量最大值索引 |
| torch.min(t) | 返回张量最小值 |
| torch.argmin(t) | 返回张量最小值索引 |
| torch.median(t) | 返回张量中位数 |
| torch.sum(t) | 返回张量求和结果 |
| torch.logsumexp(t) | 返回张量各元素求和结果,适用于数据量较小的情况 |
| torch.prod(t) | 返回张量累乘结果 |
| torch.dist(t1, t2) | 计算两个张量的闵式距离,可使用不同范式 |
| torch.topk(t) | 返回t中最大的k个值对应的指标 |
dist计算距离
dist函数可计算闵式距离(闵可夫斯基距离),通过输入不同的p值,可以计算多种类型的距离,如欧式距离、街道距离等。闵可夫斯基距离公式如下:
D
(
x
,
y
)
=
(
∑
u
=
1
n
∣
x
u
−
y
u
∣
p
)
1
/
p
D(x,y) = (\\sum^{n}_{u=1}|x_u-y_u|^{p})^{1/p}
D(x,y)=(u=1∑n∣xu−yu∣p)1/p
p取值为2时,计算欧式距离
torch.dist(t1, t2, 2)
p取值为1时,计算街道距离
torch.dist(t1, t2, 1)
比较运算函数
| 函数 | 描述 |
|---|---|
| torch.eq(t1, t2) | 比较t1、t2各元素是否相等,等效== |
| torch.equal(t1, t2) | 判断两个张量是否是相同的张量 |
| torch.gt(t1, t2) | 比较t1各元素是否大于t2各元素,等效> |
| torch.lt(t1, t2) | 比较t1各元素是否小于t2各元素,等效< |
| torch.ge(t1, t2) | 比较t1各元素是否大于或等于t2各元素,等效>= |
| torch.le(t1, t2) | 比较t1各元素是否小于等于t2各元素,等效<= |
| torch.ne(t1, t2) | 比较t1、t2各元素是否不相同,等效!= |
矩阵构造函数
| 函数 | 描述 |
|---|---|
| torch.t(t) | t转置 |
| torch.eye(n) | 创建包含n个分量的单位矩阵 |
| torch.diag(t1) | 以t1中各元素,创建对角矩阵 |
| torch.triu(t) | 取矩阵t中的上三角矩阵 |
| torch.tril(t) | 取矩阵t中的下三角矩阵 |
矩阵运算函数
| 函数 | 描述 |
|---|---|
| torch.dot(t1, t2) | 计算t1、t2张量内积 |
| torch.mm(t1, t2) | 矩阵乘法 |
| torch.mv(t1, t2) | 矩阵乘向量 |
| torch.bmm(t1, t2) | 批量矩阵乘法 |
| torch.addmm(t, t1, t2) | 矩阵相乘后相加 |
| torch.addbmm(t, t1, t2) | 批量矩阵相乘后相加 |
bmm:批量矩阵相乘
t3 = torch.arange(1, 13).reshape(3, 2, 2)
t3
tensor([[[ 1, 2],
[ 3, 4]],
[[ 5, 6],
[ 7, 8]],
[[ 9, 10],
[11, 12]]])
t4 = torch.arange(1, 19).reshape(3, 2, 3)
t4
tensor([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]],
[[13, 14, 15],
[16, 17, 18]]])
torch.bmm(t3, t4)
tensor([[[ 9, 12, 15],
[ 19, 26, 33]],
[[ 95, 106, 117],
[129, 144, 159]],
[[277, 296, 315],
[335, 358, 381]]])
addmm:矩阵相乘后相加
addmm函数结构:addmm(input, mat1, mat2, beta=1, alpha=1)
输出结果:beta * input + alpha * (mat1 * mat2)
t1
tensor([[1, 2, 3],
[4, 5, 6]])
t2
tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
t = torch.arange(3)
t
tensor([0, 1, 2])
torch.addmm(t, t1, t2, beta = 0, alpha = 10)
tensor([[300, 360, 420],
[660, 810, 960]])
矩阵的线性代数运算
| 函数 | 描述 |
|---|---|
| torch.trace(A) | 矩阵的迹 |
| matrix_rank(A) | 矩阵的秩 |
| torch.det(A) | 计算矩阵A的行列式 |
| torch.inverse(A) | 矩阵求逆 |
| torch.lstsq(A,B) | 最小二乘法 |
矩阵的分解
torch.eig函数:特征分解
特征分解中,矩阵分解形式为:
A
=
Q
Λ
Q
−
1
A = Q\\Lambda Q^{-1}
A=以上是关于深度学习基础:1.张量的基本操作的主要内容,如果未能解决你的问题,请参考以下文章