CS224W摘要10.Knowledge Graph Embeddings
Posted oldmao_2000
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了CS224W摘要10.Knowledge Graph Embeddings相关的知识,希望对你有一定的参考价值。
文章目录
CS224W: Machine Learning with Graphs
公式输入请参考: 在线Latex公式
主要内容:
1.介绍 异质图heterogeneous graph的概念和异质图经典baseline:relational GCN (RGCN),这块之前也写过一点 这块之前也写过一点,但是这里对于参数的优化讲得细些。
2.介绍 知识图谱补全knowledge graph completion 任务。
3.通过图嵌入方式的四种实现方式(TransE,TransR,DistMult,ComplEx
)及其对关系表示的限制。
Heterogeneous Graphs and Relational GCN (RGCN)
Heterogeneous Graphs
A heterogeneous graph is defined as
G
=
(
V
,
E
,
R
,
T
)
G=(V,E,R,T)
G=(V,E,R,T)
节点,边,边类型,节点类型
例子略
RGCN
先从多类型的边入手,将普通的有向图扩展为多类型的边的图结构
这里对于GNN处理有向图的公式、消息汇聚不啰嗦。
扩展后得到:
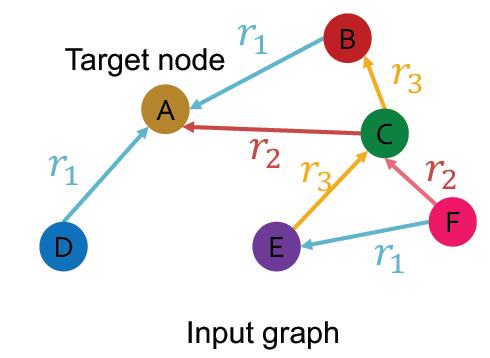
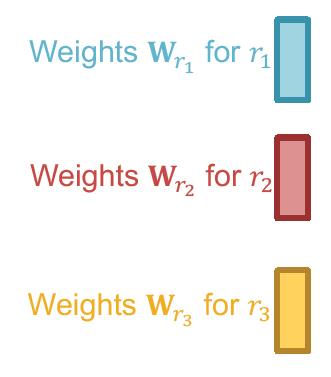
要处理不同边,那么每个类型边对应一个权重:
第l+1层的表征公式为:
h
v
(
l
+
1
)
=
σ
(
∑
r
∈
R
∑
u
∈
N
v
r
1
c
v
,
r
W
r
(
l
)
h
u
(
l
)
+
W
0
(
l
)
h
v
(
l
)
)
h_v^{(l+1)}=\\sigma\\left(\\sum_{r\\in R}\\sum_{u\\in N_v^r}\\cfrac{1}{c_{v,r}}W_r^{(l)}h_u^{(l)}+W_0^{(l)}h_v^{(l)}\\right)
hv(l+1)=σ⎝⎛r∈R∑u∈Nvr∑cv,r1Wr(l)hu(l)+W0(l)hv(l)⎠⎞
其中
W
0
(
l
)
h
v
(
l
)
W_0^{(l)}h_v^{(l)}
W0(l)hv(l)表示当前节点本身self loop
R
R
R表示当前边类型
r
r
r的集合
c
v
,
r
c_{v,r}
cv,r是归一化项是当前节点
i
i
i的邻居里面节点类型为
r
r
r的节点数量,针对这一个类型的邻居进行归一化
N
v
r
N_v^r
Nvr是当前节点
v
v
v的邻居里面节点类型为
r
r
r的节点集合
W
r
W_r
Wr表示不同边类型有自己的参数
效率分析这里之前没写,这里详细写下。
RGCN中如果有L层,那么就还有L个参数矩阵:
W
R
(
1
)
,
W
R
(
2
)
,
⋯
,
W
R
(
L
)
W_R^{(1)},W_R^{(2)},\\cdots,W_R^{(L)}
WR(1),WR(2),⋯,WR(L)
每个矩阵维度大小为:
d
(
l
+
1
)
×
d
(
l
)
d^{(l+1)}\\times d^{(l)}
d(l+1)×d(l),
d
(
l
)
d^{(l)}
d(l)是第
l
l
l个隐藏层的维度,可以看到RGCN中参数数量和关系类型数量成正比,知识图谱中关系类型数量很多,容易产生过拟合,不好训练。
这里给两个方法来解决:
block diagonal matrices
将
W
r
W_r
Wr弄成block diagonal matrices形式,使得权重矩阵变稀疏,减少非零元素个数:
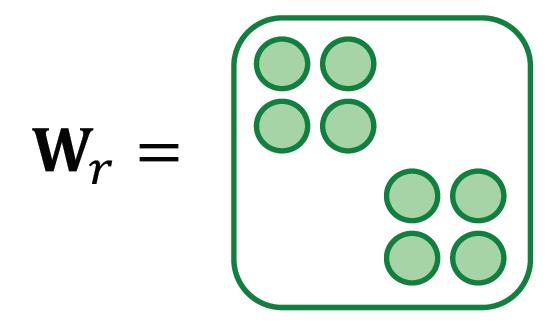
相当于用小的block在对角线上进行拼接,每个block是对应一个关系要学习的参数,如有有B个block,那么参数数量从
d
(
l
+
1
)
×
d
(
l
)
d^{(l+1)}\\times d^{(l)}
d(l+1)×d(l)减少到:
B
×
d
(
l
+
1
)
B
×
d
(
l
)
B
B\\times \\cfrac{d^{(l+1)}}{B}\\times \\cfrac{d^{(l)}}{B}
B×Bd(l+1)×Bd(l)
这个法子有一个缺点,可以看到各个block在大矩阵里面的关系是正交的,因此相互之间没有交互,也就是认为关系和关系之间是独立的,没有相互的影响。
Basis/Dictionary learning
类似提取公因式的思想,将所有的参数矩阵提取一个Share weights,然后乘以一个各个关系的常量参数:
W
r
=
∑
b
=
1
B
a
r
b
⋅
V
b
W_r=\\sum_{b=1}^Ba_{rb}\\cdot V_b
Wr=b=1∑Barb⋅Vb
这里只要学习B个常量参数
a
r
b
a_{rb}
arb即可。
Link Prediction
因为这里有多个边类型,边预测在划分数据集这里要注意一点,节点分类任务还是一样的。
这里要把不同类型的边都要分别划分成四块,因为直接随机划分会造成某种类型的边没有出现在训练集,只出现在测试集的情况,这样效果肯定扑街。
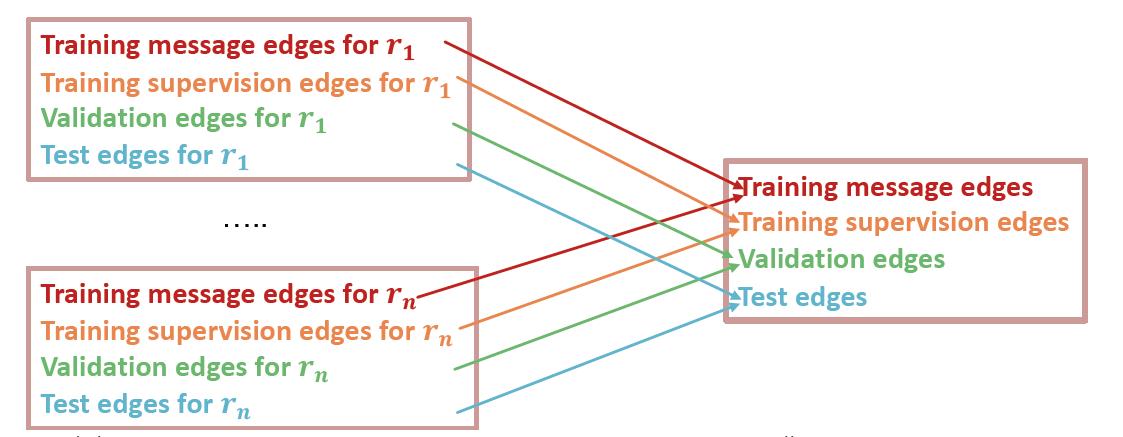
然后给出了训练和测试这个任务的例子,不展开了,里面有提到了负样本的选取原则,看论文带读笔记去吧。
Knowledge Graphs: KG Completion with Embeddings
这个小节主要是任务大概介绍,也就7分多。
知识图谱是异质图,用节点代表实体,边表示实体间的关系
下面是一个citation KG的例子:
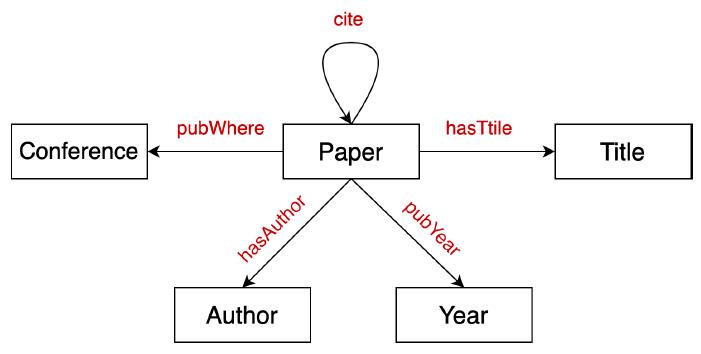
KG最常见的应用就是推理和问答。目前公开的大型KG数据集:FreeBase, Wikidata, Dbpedia, YAGO, NELL, etc.
特点:数据量大、缺少很多关系
对于以上特点的KG,是不可能遍历所有可能存在的实体的,我们还能预测可能存在却缺失的边吗?
下节讨论如何做。
Knowledge Graph Completion: TransE, TransR, DistMult, ComplEx
这里先界定图谱补全和边预测任务不一样,补全是知道部分信息(head, relation)预测剩下信息(tail),边预则是直接预测可能的链接。
例如:尼古拉斯·赵四(head)、住在(relation)预测:东北。
KG Representation
给出KG的三元组定义triples (ℎ, 𝑟, 𝑡)
head (ℎ) has relation 𝑟 with tail (𝑡)
思想是使得(ℎ, 𝑟)的embedding与𝑡的embedding越接近越好,这样预测的结果才准确。
(ℎ, 𝑟)的embedding方式
(ℎ, 𝑟)与𝑡的接近程度如何定义
上面两个问题产生了不同的模型,TransE、TransR是针对第一个问题开展的研究;DistMult, ComplEx是针对第二个问题开展的研究。下面具体看
Connectivity Patterns in (TransE vs TransR)
| Relation Patterns | Notation | Example | TransE | TransR |
|---|---|---|---|---|
| Symmetric Relations | r ( h , t ) ⇒ r ( t , h ) ∀ h , t r(h,t)\\Rightarrow r(t,h)\\space\\forall h,t r(h,t)⇒r(t,h) ∀h,t | Family, Roommate | × | √ |
| Antisymmetric Relations | ( r ( h , t ) ⇒ ¬ r ( t , h ) ) ∀ h , t (r(h,t)\\Rightarrow ¬r(t,h))\\space\\forall h,t (r(h,t)⇒¬r(t,h)) ∀h,t | Hypernym | √ | √ |
| Inverse Relations | r 2 ( h , t ) ⇒ r 1 ( t , h ) r_2(h,t)\\Rightarrow r_1(t,h) r2(h,t)⇒r1(t,h) | (Advisor, Advisee) | √ | √ |
| Composition (Transitive) Relations | r 1 ( x , y ) ∧ r 2 ( y , z ) ⇒ r 3 ( x , z ) ∀ x , y , z r_1(x,y)\\wedge r_2(y,z)\\Rightarrow r_3(x,z)\\space \\forall x,y,z r1(x,y)∧r2(y,z)⇒r3(x,以上是关于CS224W摘要10.Knowledge Graph Embeddings的主要内容,如果未能解决你的问题,请参考以下文章 |